4. Расчет конических зубчатых передач

Исходные данные: кинематическая схема передачи; крутящий момент на шестерне Т₁ и колесе Т₂, Н·м; угловая скорость шестерни ω₁ и колеса ω₂, с^-1; U – передаточное число передачи.

4.1. Выбор материала и определение допускаемых напряжений

Выполняют аналогично цилиндрическим зубчатым передачам (см. п. 3.1).

4.2. Расчет закрытых конических зубчатых передач

Так как основной причиной выхода из строя зубьев закрытых передач, работающих при обильной смазке, является усталостное контактное выкрашивание, то проектный расчет закрытых передач выполняют на контактную выносливость, а затем, после уточнения параметров передачи, проверяют действительные контактные напряжения и сравнивают их с допускаемыми с последующей проверкой зубьев на выносливость при изгибе.

При проектировочном расчете определяют предварительное значение среднего делительного диаметра шестерни d′_m1, мм

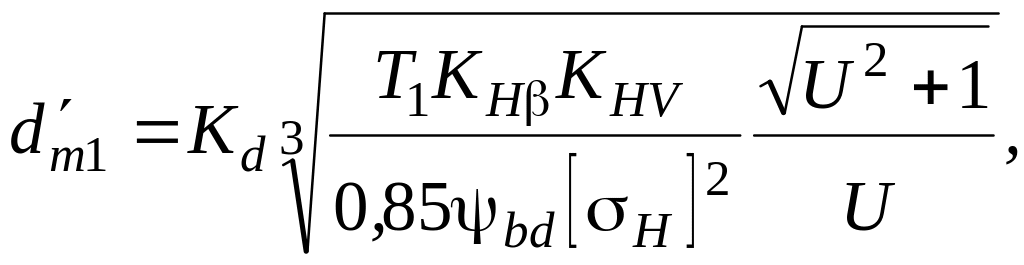(4.1)

где К_d=770 МПа^1/3 – для прямозубых передач;

К_d=680 МПа^1/3 – для косозубых передач;

ψ_bd – коэффициент ширины зубчатого венца шестерни относительно ее среднего делительного диаметра ψ_bd=b/d_m1=0,3÷0,6;

K_Hβ – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца, зависящий от твердости и расположения колес относительно опор (рис. 3.2 а, б – схемы 1, 2);

K_HV – коэффициент внешней динамической нагрузки (табл. 3.3).

Ширина венца зубчатых колес b, мм, (рис. 4.1) определяется по формуле

Величина b округляется до целых чисел.

Угол делительного конуса, град

δ′₁ = arctg(1/U).

Внешнее конусное расстояние, мм

R′_e=0,5(d′_m1/sinδ′₁+b), при этом необходимо, чтобы выполнялось условие (b/R′_e≤0,3).

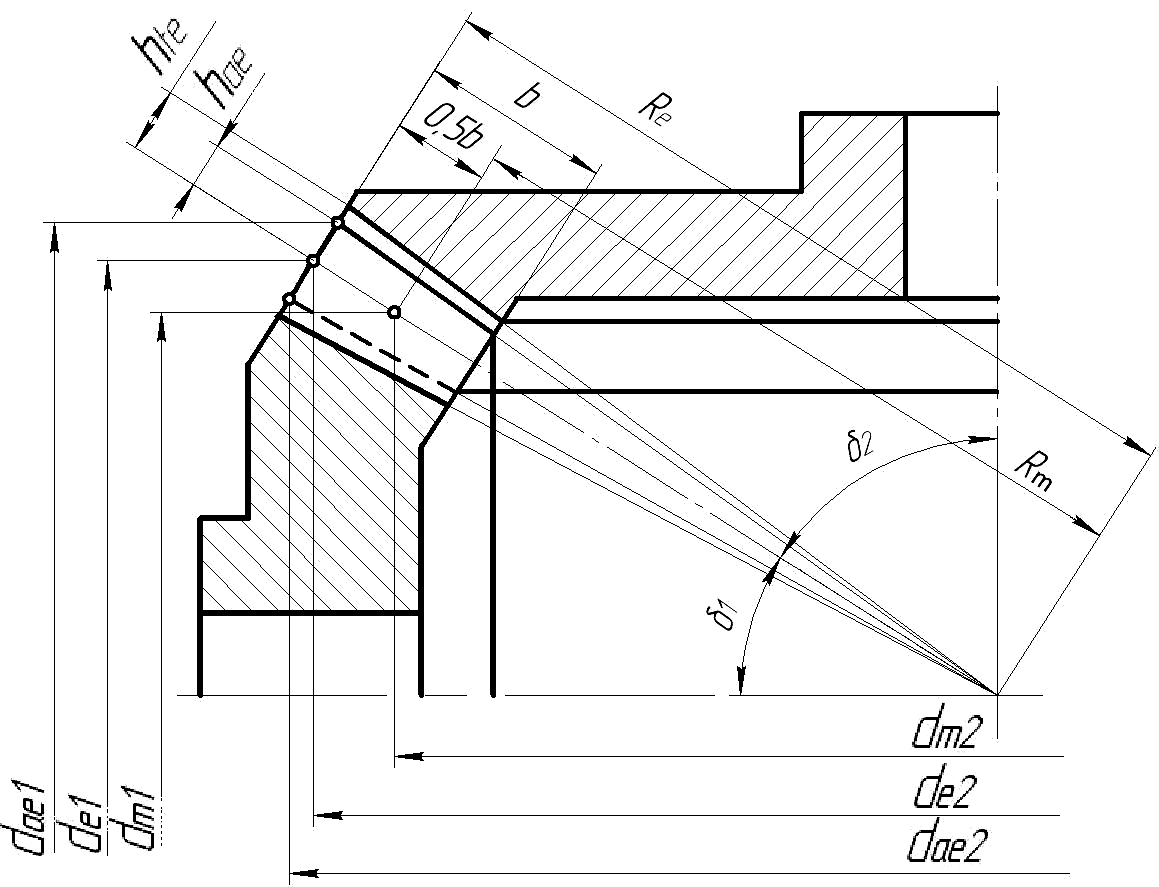
Рис. 4.1. Основные параметры конической передачи

Внешний делительный диаметр шестерни, мм

d′_e1=d′_m1R′_e/(R′_e-0,5b).

Предварительно принимая z₁=17 (табл. 4.1), определяют внешний окружной модуль зацепления m′_te= d′_e1/Z′₁, мм и округляют до ближайшей величины m_te=m_n, мм в соответствии с табл. 3.5. При этом необходимо, чтобы выполнялось условие (m_te≥(1/8÷1/10)b).

Таблица 4.1

Рекомендуемое минимальное число зубьев колеса

Число зубьев шестерни Z1	12	13	14	15	16	17
Наименьшее число зубьев колеса Z2	30	26	20	19	18	17

Определяется число зубьев шестерни Z₁=d′_e1/m_te. Число зубьев колеса Z₂=Z₁U. Причем, Z₁ и Z₂ – целые числа. Уточняют истинное передаточное число U=Z₂/Z₁. Отклонение u от заданного значения не должно превышать ±3%.

Действительные величины углов делительных конусов, град

δ₁=arctg(Z₁/Z₂); δ₂=arc tg(Z₂/Z₁).

Действительное внешнее конусное расстояние, мм

R_e=0,5m_te

Средний модуль зацепления, мм

m_m=m_te(R_e-0,5b)/R_e.

Средний делительный диаметр

шестерни d_m1= m_mZ₁;

колеса d_m2= m_mZ₂.

4.3. Проверочный расчет зубьев по контактным напряжениям

Окружная сила в зацеплении, Н F_t=2T₁/d_m1.

Окружная скорость колес, м/с v=π d_m1n₁/(60·10³).

Степень точности принимается по табл. 3.6.

Расчетные контактные напряжения определяются по формуле, МПа

(4.2)

где – коэффициент, учитывающий форму сопряженных поверхностей зубьев, принимается равным 1,77;

– коэффициент, учитывающий механические свойства материала сопряженных зубчатых колес, принимается равным 275;

– коэффициент, учитывающий суммарную длину контактных линий, принимаемый равным = 0,9.

Удельная окружная динамическая сила, Н/мм

W_Hv=δ_H g₀ V

где δ_H – коэффициент, учитывающий влияние вида зубчатой передачи и модификации профиля зуба на динамическую нагрузку (табл. 4.2);

g₀ – коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса (табл. 4.3);

Таблица 4.2