
- •Физические основы механики
- •1. Кинематика поступательного движения
- •1. Основные понятия кинематики
- •2. Скорость
- •3. Ускорение
- •4. Уравнения равнопеременного движения
- •5. Стандартный график движения поезда
- •2. Силы в механике
- •1. Сила тяжести и вес тела
- •2. Силы трения покоя и скольжения
- •3. Аэродинамические силы
- •4. Сила упругости
- •3. Силы в транспорте
- •1. Сила тяги локомотива
- •2. Зависимость силы тяги от скорости
- •3. Сила трения качения
- •4. Сила торможения
- •4. Динамика поступательного движения
- •1. Законы Ньютона
- •2. Движение поезда в режиме постоянной силы тяги
- •3. Движение поезда в режиме постоянной мощности
- •4. Движение поезда при торможении и выбеге
- •5. Неинерциальные системы отсчета
- •Силы инерции
- •2. Движение вагона на повороте
- •3. Опрокидывание вагона на повороте.
- •4. Силы в автосцепках вагонов
- •6. Статика
- •1. Условие равновесия тел
- •2. Сила давления вагона на рельсы
- •3. Стоянка поезда на спуске
- •4. Балластировка локомотива
- •7. Законы сохранения в механике
- •1. Закон сохранения импульса
- •2. Работа
- •3. Кинетическая энергия
- •4. Потенциальная энергия
- •5. Закон сохранения энергии
- •8. Соударение тел
- •1. Явление удара
- •2. Соударение тел
- •3. Сцепление вагонов
- •Параметры кинематики вращательного движения
- •2. Момент силы
- •3. Основной закон динамики вращательного движения
- •4. Расчет момента инерции некоторых тел
- •10. Динамика плоского движения тел
- •1. Движение центра масс
- •1. Плоское движение твердых тел
- •3. Теорема Штейнера
- •4. Ускорение при скатывании вагона
- •11. Кинетическая энергия вращателього
- •1. Кинетическая энергия вращательного движения
- •2. Кинетическая энергия при плоском движении тела
- •3. Скатывание вагона с сортировочной горки
- •4. Аккумулирование энергии маховиком
- •12. Закон сохранения момента импульса
- •1. Момент импульса
- •2. Закон сохранения момента импульс для одного тела
- •3. Закон сохранения момента импульса для системы тел
- •4. Гироскоп
- •13. Релятивистская механика
- •1. Постулаты сто
- •2. Преобразования Лоренца
- •3. Следствия преобразований Лоренца
- •3. Основы релятивистской механики
- •4. Радиолокационный скоростемер.
- •14. Механические колебания
- •1. Уравнение гармонических колебаний.
- •2. Пружинный маятник
- •3. Физический маятник
- •4. Галопирующие колебания вагона
- •15. Затухающие колебания
- •1. Уравнение затухающих колебаний
- •2. Параметры затухания колебаний
- •3. Амортизаторы вагона
- •4. Рессорное подвешивание вагона
- •16. Вынужденные колебания
- •1. Уравнение вынужденных колебаний
- •2. Вибрация электродвигателя
- •17. Волны в упругих средах
- •1. Уравнение волны.
- •2. Интерференция волн
- •3. Скорость распространения упругих волн
- •4. Колебания контактного провода
- •1. Кинематика поступательного движения…………………… …………...………7
2. Вибрация электродвигателя
Вибрация тяговых электродвигателей это вынужденные колебания, вызванные действием центробежной силы на несбалансированный якорь двигателя. Если частота вращения якоря совпадет с частотой собственных колебаний двигателя, то наступает явление резонанса, при котором амплитуда колебаний двигателя может достичь большой величины. Поэтому, устанавливая амортизаторы, следует так подбирать упругость пружин подвески, чтобы не было резонанса.
Определим центробежную силу инерции. Якорь – не болванка, а сложная конструкция и изготовить ее идеально точно крайне затруднительно. Центр масс якоря может быть смещен относительно оси вала на некоторое расстояние r0. Уменьшают этот разбаланс методом статической балансировки, добиваясь при строго горизонтальной оси якоря безразличного равновесия в любом положении. Однако, возможно, что у одной части якоря ее центр масс находится по одну сторону оси вала, а у другой – по другую, хотя общий может быть на оси. Тогда при вращении возникает переменный момент сил. Его устраняют методом динамической балансировки, уравновешивая каждую часть якоря дополнительными грузами.
Ограничимся
действием только центробежной силы
инерции. Ее равнодействующая приложена
к центру масс. Величина центробежной
силы равна
![]() ,
где mяк
– масса
якоря, ωяк
– угловая
скорость
вращения якоря, r
– расстояние
от оси вращения до центра масс якоря.
Вектор силы вращается вместе с якорем.
В проекции
на вертикальное направление, вдоль
которого происходят колебания двигателя,
центробежная сила становится периодической
силой, вызывающей вынужденные колебания
двигателя с циклической частотой, равной
скорости вращения якоря:
,
где mяк
– масса
якоря, ωяк
– угловая
скорость
вращения якоря, r
– расстояние
от оси вращения до центра масс якоря.
Вектор силы вращается вместе с якорем.
В проекции
на вертикальное направление, вдоль
которого происходят колебания двигателя,
центробежная сила становится периодической
силой, вызывающей вынужденные колебания
двигателя с циклической частотой, равной
скорости вращения якоря:
![]() . (16.9)
. (16.9)
Амплитуда колебаний двигателя относительно вагона рассчитывается по формуле (6), при подстановке амплитуды центробежной силы
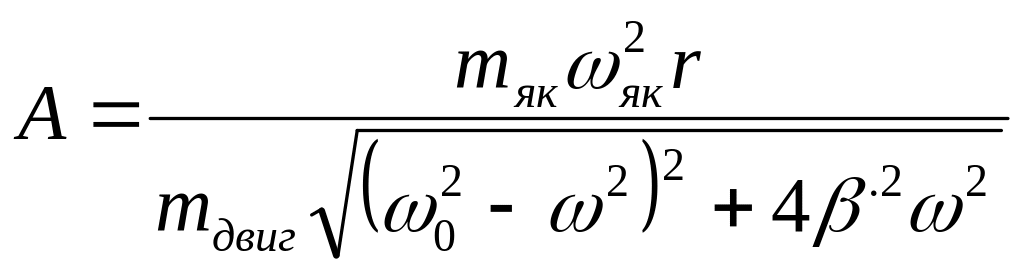 . (16.10)
. (16.10)
Проблема в приведенных расчетах заключается в том, что вал при вращении под действием центробежной силы изгибается, и расстояние от оси вращения до центра масс r не постоянно, оно зависит от скорости вращения. При малой скорости вращения центробежная сила увеличивает изгиб вала. Если частота вращения оказывается равна частоте собственных колебаний якоря на валу, наступает резонанс и расстояние центра масс от оси вращения наибольшее. А при очень большой скорости вращения сила и смещение оказываются в противофазе, как это должно быть при вынужденных колебаниях якоря на валу, и смещение стремится к нулю. Вибрации при этом почти исчезают.
Таким образом, тяговый электродвигатель может иметь даже две резонансных частоты: при колебаниях двигателя как целого в подвеске и при колебаниях якоря относительно корпуса двигателя. Если же резонанс наступил, то следует быстрее увеличить скорость вращения и пройти опасный диапазон.
Задачи
1. Определить, при какой скорости вагон начнет сильно раскачиваться в вертикальном направлении из-за ударов о стыки рельсов. Масса вагона 60 т, коэффициент упругости восьми пружин подвески 2·107 Н/м, длина рельса 25 м.
2. Центр масс ротора массой 400 кг тягового двигателя массой 800 кг смещен относительно оси вращения на 0,01 мм. Двигатель подвешен к раме вагона, коэффициент упругости подвески 8·105 Н/м. При какой частоте вращения наступит резонанс. Определить амплитуду колебаний при резонансе, если коэффициент затухания амортизаторов 0,8 1/с.
3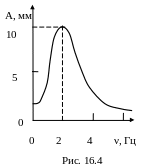 . Определить
амплитуду вынуждающей силы вибростенда
по графику зависимости амплитуды от
частоты вынужденных колебаний (рис.16.4)
колесной пары массой 1200 кг, установленной
с пружинами подвески на вибростенде.
Коэффициент затухания колебаний 0,3 1/с
. Определить
амплитуду вынуждающей силы вибростенда
по графику зависимости амплитуды от
частоты вынужденных колебаний (рис.16.4)
колесной пары массой 1200 кг, установленной
с пружинами подвески на вибростенде.
Коэффициент затухания колебаний 0,3 1/с
4. Колесная пара массой 1300 кг с подвеской
установлена на вибростенде. Определить
приближенно по графику (рис.16.4) коэффициент
затухания амортизаторов как полуширину
резонансного пика на уровне
![]() .
Определить коэффициент упругости
пружин подвески.
.
Определить коэффициент упругости
пружин подвески.
5. На вагон массой 40 т со стороны рельсов действует вертикальная переменная сила F = 300 sin 31,4 t Н. При каком значении коэффициента упругости подвески вагона наступит резонанс. Чему равна при этом амплитуда колебаний, если коэффициент затухания 0,4 1/с.
6. Определить, при какой скорости начнет сильно раскачиваться вагон, совершая галопирующие колебания из-за ударов о стыки рельсов. Масса вагона 60 т, расстояние между осями 12 м, длина вагона 15м, коэффициент упругости передней и задней подвесок 1·107 Н/м. Длина рельса 25 м.
7. Определить, при какой амплитуде колебаний вагона при вибрации с частотой 20 Гц незакрепленные предметы будут подпрыгивать относительно пола вагона.
