1.1.7 Формы токов биполярного транзистора с учетом его
инерционности при возбуждении от источника напряжения
Рассчитаем временные зависимости токов транзистора [1], принимая, как и ранее, что напряжение на входе является гармоническим
,
(1.14)
В
соответствии со схемой, приведенной на
рис.1.15,
для определения формы импульсов токов
,
необходимо найти
зависимость
.
Составим
уравнение для
,
полагая
.
Введем постоянные времени входной цепи открытого и закрытого транзистора
,
(1.15)
и
параметр
.
Угол
отсечки
называется низкочастотным, так как
он определяет
отсечку тока коллектора при
.
Заменив в (1.7)
нелинейную
зависимость
кусочно-линейной (1.8), получим
дифференциальное уравнение относительно
для открытого
и закрытого транзистора
;
(1.16)
.
При
напряжение на переходе
в области отсечки
равно входному и транзистор открывается
при
.
В этот момент
становится равным
и продолжает возрастать.
Поэтому вступает в силу первое уравнение
(1.16). Его решение
при начальном условии
имеет вид
,
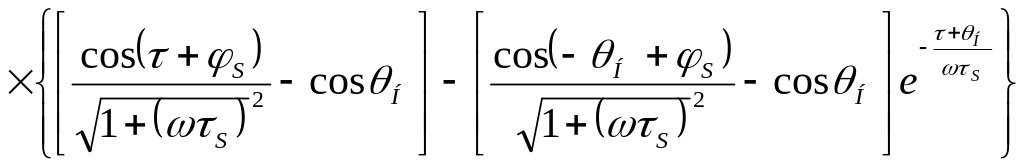(1.17)
где
.
Решение
содержит вынужденную
(первое слагаемое в фигурных скобках)
и свободную
(второе слагаемое) составляющие.
Амплитуда
и фаза
вынужденной
составляющей определяются модулем и
фазой коэффициента
передачи напряжения
в активной области:
(1.18)
Временные диаграммы
напряжения на переходе
,
его составляющих
и токов
,
,
рассчитанные при
по (1.9), (1.10), показаны
на рис.1.16.
Из
рис.1.16,
а видно, что транзистор открывается в
момент
,
когда
.
На
низких частотах
транзистор закрылся
бы при
.
Однако на высоких частотах импульс
напряжения
в активной области и повторяющий его
форму импульс
тока
(1.9) имеют затянутый фронт (
при
),
что обусловлено
процессом заряда диффузионной
емкости. Максимумы этих импульсов
запаздывают относительно
максимума
на угол
,
несколько меньший величины
.
В результате
транзистор запирается позже, при
,
и импульс тока
расширяется.
Базовый ток на рис.1.16,г
построен
как сумма двух составляющих,
одна из которых пропорциональна
напряжению
,
другая
- производной
от него.
Первая
составляющая
есть
ток через сопротивление
,
вторая
- зарядный ток диффузионной емкости,
причем
,
когда
,
т.
е. емкость разряжается.
Это обусловливает отрицательный выброс
в токе базы.
Отрицательный
выброс наблюдается и в эмиттерном токе,
поскольку
(рис.1.16,д).
Характерным
для рассматриваемых диаграмм является
момент,
соответствующий углу
,
когда напряжение на переходе
и
ток коллектора
принимают максимальные значения. Угол
определяется из
условия
.
При
первое слагаемое
в (1.16) пропадает, что позволяет записать
,
(1.19)
откуда
согласно (1.9) и равенству
получим
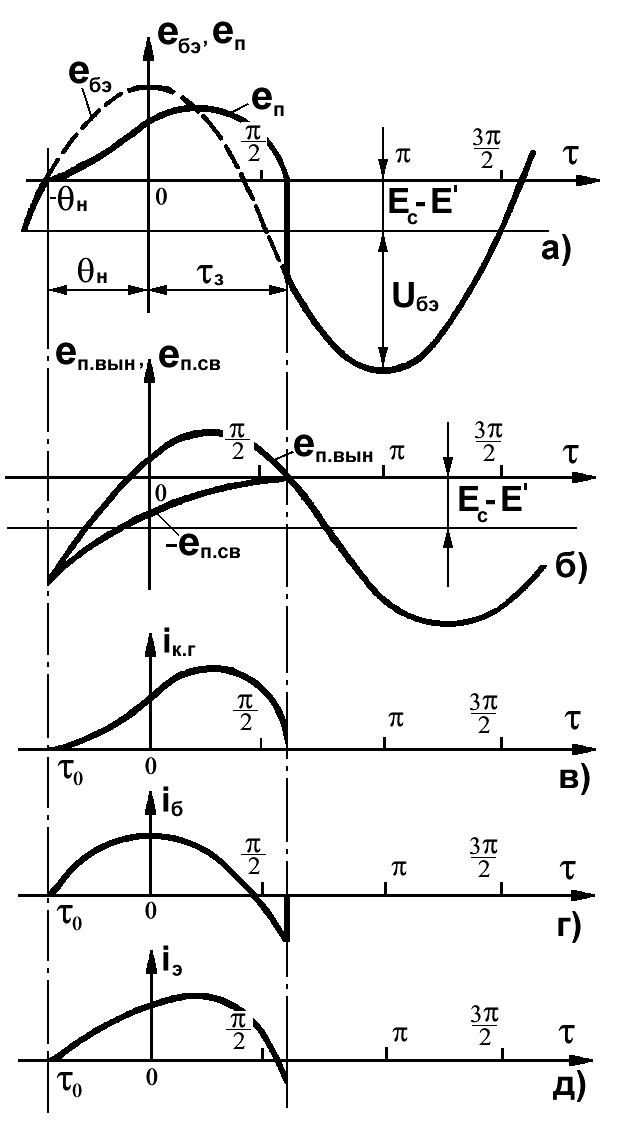
Рисунок 1.16 – Временные
диаграммы напряжения на входе
, эмиттерном переходе
,
токов коллектора
,
базы
и эмиттера
при возбуждении биполярного транзистора
от генератора напряжения
Зависимости угла запирания
, момента максимума
от
угла отсечки
при разных значениях
приведены на рис.1.17.
Штрихпунктирными
линиями показаны границы перехода
транзистора в
линейный режим работы (класс А).
Как видно, при уменьшении угла отсечки
,
уменьшаются от своих граничных значений
до нуля при
.
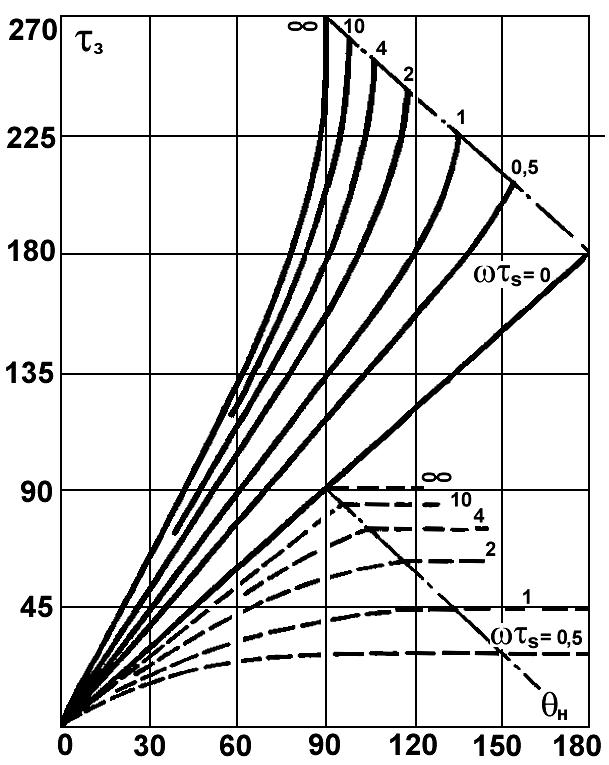
Рисунок 1.17 – Зависимости угла запирания
(сплошные линии),
момента максимума
(штриховые
линии) от угла отсечки