1.1.3 Гармонический анализ косинусоидальных импульсов

Найдем гармоники косинусоидальных импульсов выходного тока в недонапряженном и критическом режимах [1,2]. Последовательность импульсов выходного тока можно представить рядом Фурье.

Здесь - постоянная составляющая выходного тока; - амплитуды первой, второй, третьей и т.д. гармоник выходного коллекторного тока транзистора.

Имея аналитические выражения для , значения , определим по формулам для коэффициентов ряда Фурье:

;

Постоянная составляющая выходного тока

,

где

.

Амплитуда -й гармоники выходного тока

,

где

,

,

.

Иногда необходимо оценить влияние угла отсечки на гармоники тока по известной амплитуде импульса выходного тока .

В этом случае составляющие выходного тока находятся через коэффициенты , называемые коэффициентами Берга

,

где .

При расчете КПД выходной цепи часто используются коэффициент формы коллекторного тока по первой гармонике

.

Коэффициенты , и подробно табулированы. На рис.1.6 а,б приведены графики зависимостей и для постоянной составляющей и первых трех гармоник, а также зависимости .

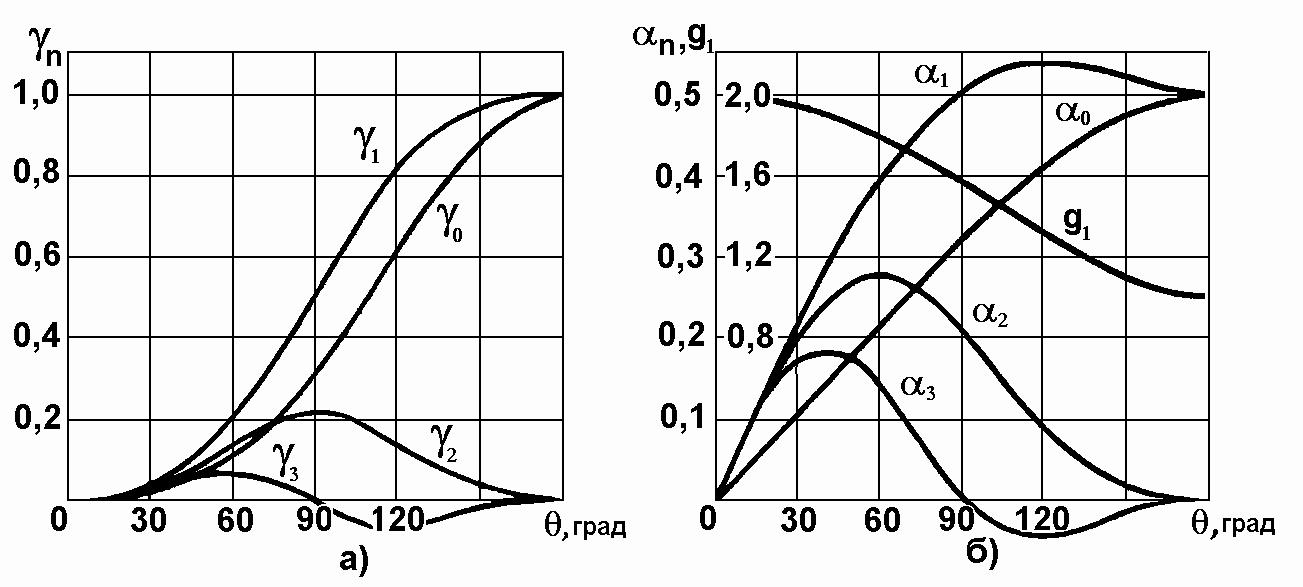
Рисунок 1.6 – Графики коэффициентов Берга

Отрицательное значение коэффициентов и при углах отсечки означает, что ток третьей гармоники имеет противоположную начальную фазу по сравнению с током первой гармоники.

Приведенные графики наглядно характеризуют гармонический состав коллекторного тока при различных . Так как (колебания класса А) амплитуда первой гармоники равна постоянной составляющей ; амплитуды второй, третьей и т.д. гармоник равны нулю. В области графики и при имеют максимумы; для коэффициентов значение угла , при котором наблюдается максимум, вычисляется из выражения .

Из графиков (рис.1.6) следует, что для получения высокого КПД целесообразно, чтобы угол отсечки находился в пределах . При меньших углах отсечки коэффициент формы , а, следовательно, и КПД возрастают незначительно. При заданной амплитуде импульса выходного тока полезная максимальная мощность получается, когда угол отсечки , т.к. коэффициент принимает максимальное значение. КПД в этом случае сравнительно высокий. Очень часто угол отсечки выбирается исходя из других требований, в частности, из требований к нелинейным искажениям. Выбор оптимального угла отсечки требует конкретных условий работы ГВВ и, как правило, является компромиссным.

1.1.4 Нагрузочные характеристики генератора с внешним возбуждением

Рассмотрим зависимости токов транзистора, напряжений на нем и энергетических показателей от сопротивления нагрузки [1-2] при неизменных значениях напряжений возбуждения , смещения , коллекторного питания , т.е. нагрузочные характеристики. Они используются при настройке ГВВ и оценке влияния на его режим изменений параметров фидера и антенны. Примем пока, что сопротивление нагрузки вещественное: .

При изменении меняется амплитуда напряжения на коллекторе: . Как было показано в предыдущих разделах, амплитуда , в свою очередь, зависит от . Каждой точке этой зависимости соответствует свое значение . Принимая за аргумент, строим зависимости и, т. е. нагрузочные характеристики для тока и напряжения (рис.1.7,а). С ростом сопротивления нагрузки сначала медленно убывает, а транзистор работает в недонапряженном режиме. При наступает критический режим. При дальнейшем увеличении напряжение превышает и медленно растет, транзистор переходит в перенапряженный режим, в импульсе коллекторного тока появляется провал и падает.

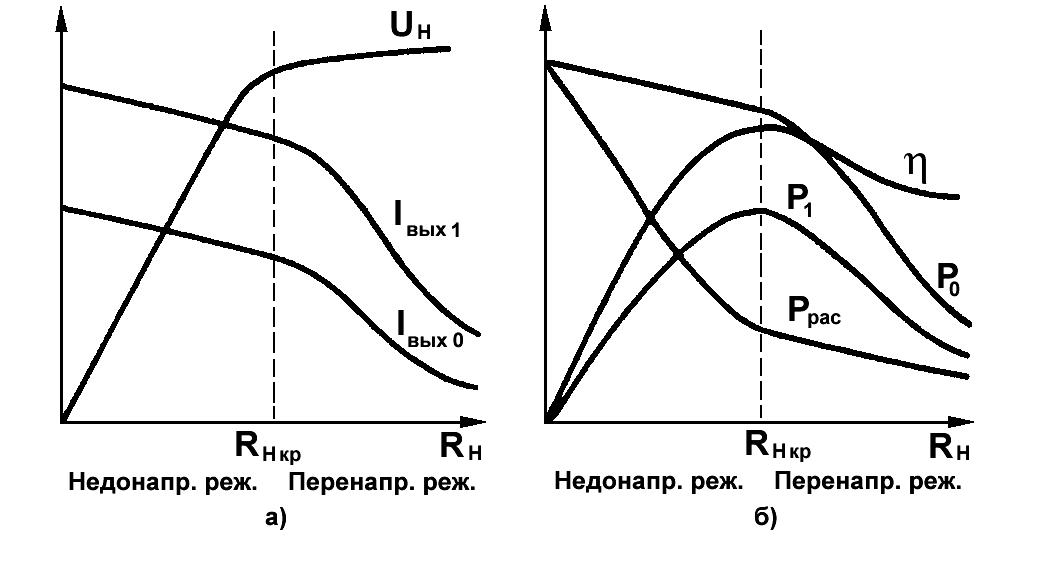
Рисунок 1.7 – Зависимость параметров ГВВ от сопротивления нагрузки

Как видно из рис.1.7, ток меняется пропорционально первой гармонике поскольку коэффициент формы в недонапряженном режиме постоянен, а в перенапряженном режиме медленно уменьшается. Входной базовый ток в перенапряженном режиме растет с увеличением нагрузки .

На рис.1.7,б представлены зависимости мощностей , , от сопротивления нагрузки . Здесь - потребляемая мощность, - полезная мощность, - мощность, рассеиваемая на коллекторе транзистора.

Поскольку , зависимость повторяет по форме . Полезная мощность , как видно из рис.1.7, возрастает примерно пропорционально в области, где , имеет максимум вблизи точки и убывает с ростом в перенапряженном режиме.

Поведение как функции от определяется формулой . При вся мощность, потребляемая от источника, рассеивается на выходном электроде активного элемента. С ростом она убывает быстро при и медленно при . При расстроенной нагрузке, когда , активный элемент может оказаться в тяжелом тепловом режиме. Поэтому каскад настраивают при пониженных значениях и .

Коэффициент использования напряжения коллекторного питания повторяет зависимость , так как и . Коэффициент формы в недонапряженном режиме можно считать постоянным, так как угол отсечки меняется мало. В перенапряженном режиме убывает с ростом из-за появления провала в импульсе тока, но значительно медленнее, чем поскольку тоже уменьшается. Поэтому коэффициент полезного действия имеет весьма тупой максимум, лежащий в области перенапряженного режима.

Анализ нагрузочных характеристик позволяет сделать заключение о том, что критический режим является оптимальным для активного элемента по полезной мощности , коэффициенту полезного действия и коэффициенту усиления по мощности.