8. Інтеграл площ.

Рівняння (1.14) незбуреного руху помножимо векторно на вектор , отримаємо:

Інтегруючи цей вираз отримаємо:

, (1.16)

(1.16) є рівнянням, яке називають інтегралом площ. Розпишемо його в координатній формі:

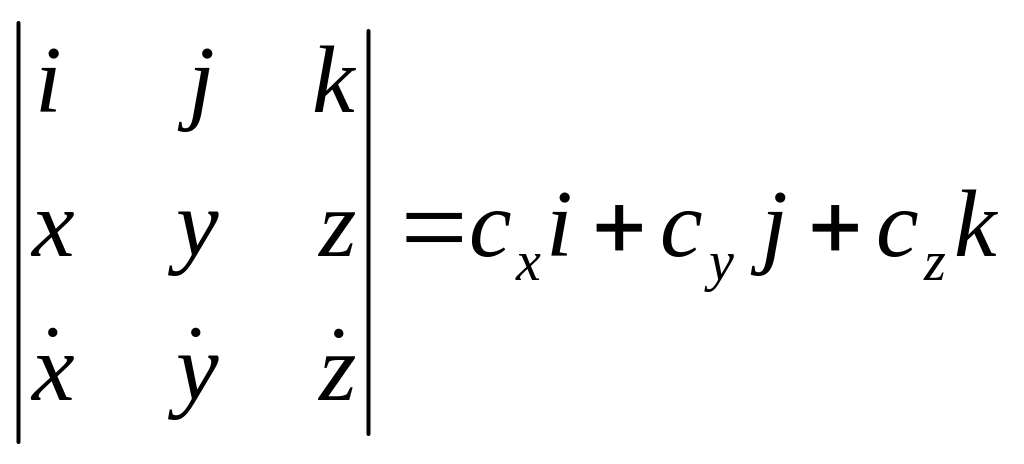
Знайдемо координатні рівняння, що характеризують інтеграл площі:

, (1.17)

(1.17) називаються інтегралом площ в координатній формі.

Отримаймо рівняння, що характеризує в координатній формі площину орбіти супутника.

Нехай координати супутника x, y, z, помножимо на рівняння (1.17) і просумуємо.

, (1.18)

Рівняння (1.18) називають рівнянням площини орбіти супутника в координатній формі.

9. Інтеграл енергії

Помножимо рівняння (1.14) скалярно на величину , отримаємо:

, (1.19)

Оскільки і є направлені один по одному то, то косинус між ними дорівнює 1. праву частину вихідного рівняння перетворимо наступним чином:

, (1.20)

Підставимо (1.20) і (1.19) в вихідне рівняння:

Інтегруємо отриманий вираз:

, (1.21)

Рівняння (1.21) називають інтегралом енергії. Воно характеризує ту енергію, яку має супутник рухаючись по орбіті. При чому в (1.21) V характеризує кінетичну енергію супутника, а потенціальну енергію супутника. Інтеграл енергії можна отримати і в такому вигляді:

, (1.22)

Перетворимо праву частину в (1.22) виходячи з того, що для характеристики положення супутника на орбіті можна використовувати фокальний параметр

, (1.23)

Підставляючи замість в (1.22) його вираз з (1.23)

, (1.24)

10. Дослідження інтегралу енергії

Проаналізуємо отримані формули інтеграла енергії для характеристик початкової швидкості ШСЗ для виведення його на ту чи іншу орбіту.

1-й: нехай орбітою є коло (e=0). Підставимо в (1.24), отримаємо:

, (1.24)

, (1.25)

Відомо, що радіус вектор супутника і фокальний параметр пов’язані між собою таким рівнянням:

– істинна аномалія

Для підставляючи в (1.25) отримаємо:

, (1.26)

Замінимо в (1.21) h його значенням із (1.26)

, (1.27)

Якщо прийняти , , то

– перша космічна швидкість.

2-й: – парабола. Замінимо цим виразом значення в (1.21)

, (1.21)

, (1.28)

– друга космічна швидкість.

3-й:орбітою є еліпс

, (1.29)

Якщо початкова швидкість буде знаходитись в границях між 7,9 і 11,2, то супутник біде виведений на орбіту у вигляді еліпса.

4-й: нехай орбітою є гіпербола.

, (1.30)

Знаючи, що – друга космічна швикість ми виведемо такий супутник на гіперболічну орбіту. Можна доказати, що для того щоб супутник вийшов за межі сонячної системи треба надати швидкість більше третьої космічної

11. Інтеграли Лапласа

Запишемо диференційне рівняння незбуреного руху:

Помножимо векторно на інтеграл площ

Відомо, що , тоді замінимо цим виразом праву частину

, (1.31)

Зробимо відповідні заміни

Замінимо отриманим виразом праву частину (1.31)

Інтегруємо:

, (1.32)

(1.32) – інтеграл Лапласа в векторній формі.

Представимо (1.32) в координатній формі:

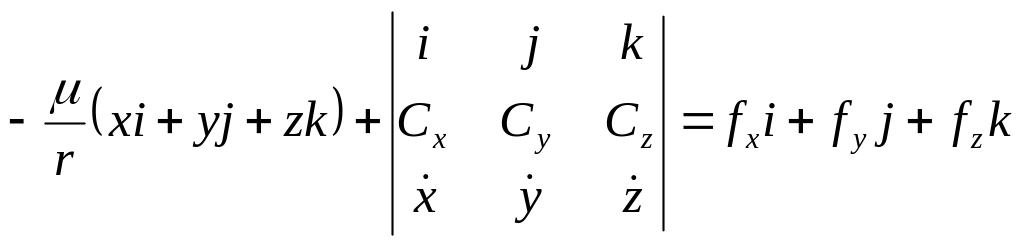, (1.33)

(1.33) є записом рівняння Лапласа в координатній формі. Розпишемо його по окремих координатах:

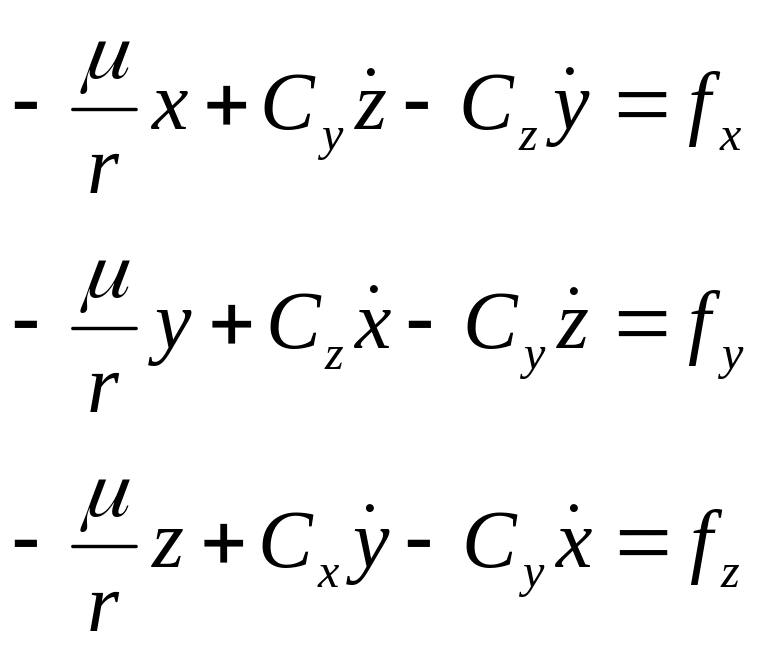, (1.34)

Рівняння Лапласа дозволяє отримати формулу інтеграла енергії. Для цього скакярно помножимо (1.32) на вектор f. В результаті перетворень:

, (1.35)