
- •Электротехника
- •Электротехника: лабораторный практикум/ Попов, а.П., Татевосян, а.С., Завьялов, е.М., Батрак, а.И., Хамитов, р.Н. Омск: Изд – во ОмГту, 2008 г. 85 с.
- •Введение
- •Описание лабораторного стенда
- •Теоретической и общей электротехники
- •Указания к монтажу электрических схем.
- •Техника безопасности при проведении лабораторных работ.
- •Лабораторная работа № 1 изучение лабораторного стенда по электротехнике
- •Краткие теоретические сведения
- •Лабораторная работа № 2 линейные электрические цепи синусоидального тока
- •Краткие теоретические сведения
- •Лабораторная работа № 3 резонанс напряжений
- •Краткие теоретические сведения
- •Лабораторная работа № 4 резонанс токов
- •Краткие теоретические сведения
- •Лабораторная работа № 5 исследование трехфазной цепи при соединении приемников электрической энергии «звездой» и «треугольником»
- •Краткие теоретические сведения
- •Лабораторная работа № 6 исследование тягового усилия электромагнита
- •Краткие теоретические сведения
- •Лабораторная работа № 7 однофазный трансформатор
- •Краткие теоретические сведения
- •Лабораторная работа № 8 трансформатор тока
- •Краткие теоретические сведения
- •Электротехника Лабораторный практикум
Лабораторная работа № 4 резонанс токов
Цель работы: Установление условий возникновения резонанса токов. Исследование частотных зависимостей напряжений на элементах параллельного резонансного контура.
Домашнее задание
Напишите формулы для определения активной, индуктивной, емкостной и полной проводимостей электрической цепи.
Дайте определение резонанса токов.
Как можно установить наличие резонанса токов в электрической цепи?
Чем отличается резонанс токов от резонанса напряжений?
Поясните, оказывает ли влияние на потребляемую активную мощность, параллельно включенная в электрическую цепь емкость.
Краткие теоретические сведения
В электрических цепях переменного тока при параллельном соединении реактивных сопротивлений может возникнуть резонанс токов. Это происходит в том случае, когда в одних ветвях преобладает реактивное индуктивное сопротивление, а в других – реактивное емкостное сопротивление. При взаимной компенсации реактивных токов в параллельно включенных элементах возникающий резонанс называется резонансом токов.
Характерные
особенности резонанса токов проанализируем
на примере параллельного колебательного
контура с потерями энергии, обусловленными
резисторами (рис. 1). Для упрощения анализа
в параллельный контур введем резисторы
с одинаковыми сопротивлениями
![]()
Эквивалентная проводимость параллельного контура между точками «a» и «b» определяется выражением
![]()
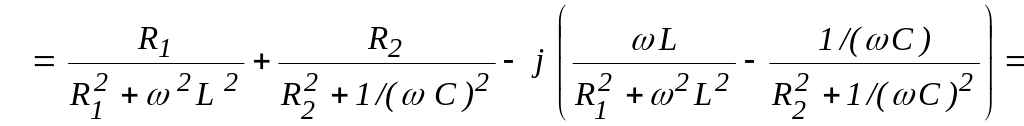
![]()
Условие резонанса
определяется равенством нулю мнимой
части входной проводимости параллельного
резонансного контура
![]() .
Заменяя в выражении
.
Заменяя в выражении
![]() угловую частоту
угловую частоту
![]() на резонансную частоту
на резонансную частоту
![]() ,
условие резонанса перепишем в виде
,
условие резонанса перепишем в виде
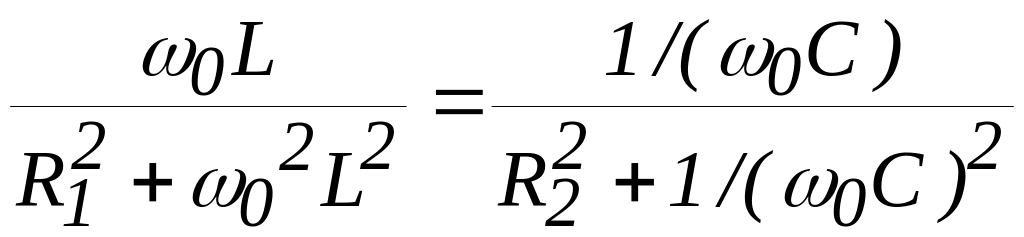 .
.
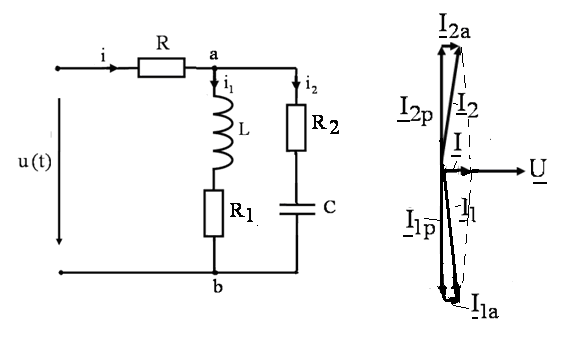
Рис. 1 Рис.2
Решение уравнения относительно дает выражение

где
![]() – волновое (характеристическое)
сопротивление.
– волновое (характеристическое)
сопротивление.
В идеальном контуре,
когда
![]() резонансная частота
резонансная частота
![]() принимает такое же значение, как и в
последовательном резонансном контуре.
Ток на неразветвленном участке цепи
протекать не будет, так как
принимает такое же значение, как и в
последовательном резонансном контуре.
Ток на неразветвленном участке цепи
протекать не будет, так как
![]() .
.
При резонансе эквивалентное сопротивление параллельного контура между точками «a» и «b» определяется выражением

Если активные
сопротивления, включенные в параллельные
ветви не равны между собой, то выражения
для расчета
![]() и
и
![]() получаются более сложными.
получаются более сложными.
Ток на неразветвленном участке цепи при резонансе определяется выражением
![]() .
.
Токи в параллельных ветвях при резонансе определяются, используя закон Ома
![]()
![]() .
.
При малых значениях
сопротивлений
![]() и
и
![]() ,
когда выполняются неравенства
,
когда выполняются неравенства
![]() и
и
![]() ,
угол сдвига фаз между токами
,
угол сдвига фаз между токами
![]() и
и
![]() будет равен
будет равен
![]() .
При этом из векторной диаграммы (рис.
2) видно, что ток
будет отставать по фазе от напряжения
.
При этом из векторной диаграммы (рис.
2) видно, что ток
будет отставать по фазе от напряжения
![]() почти на 90 0,
а ток
– соответственно опережать напряжение
почти на угол
почти на 90 0,
а ток
– соответственно опережать напряжение
почти на угол
![]()
Описание лабораторного стенда и рабочее задание
Собрать схему параллельного резонансного контура, используя съемную панель лабораторного стенда (рис. 3) и расположенные на ней тумблеры
 –
–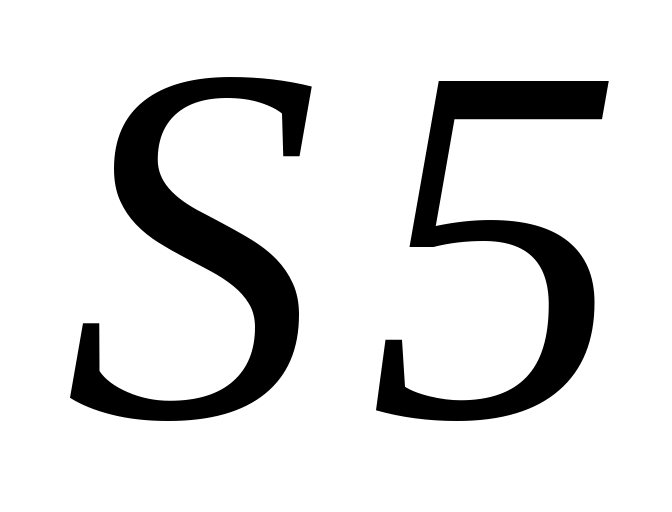 .
Внимание!
При
сборке схемы с помощью тумблеров
следует
учитывать, что перевод тумблера в
верхнее положение соответствует
замыканию ключа на участке цепи.
.
Внимание!
При
сборке схемы с помощью тумблеров
следует
учитывать, что перевод тумблера в
верхнее положение соответствует
замыканию ключа на участке цепи.
На съемной панели параметры цепи таковы:
![]() ,
,
,
,
![]() ,
,
![]() .
.
Подключить схему непосредственно к генератору низкой частоты (ГНЧ). Установить с помощью ручки управления ГНЧ и вольтметра PV1 действующее значение напряжения в диапазоне
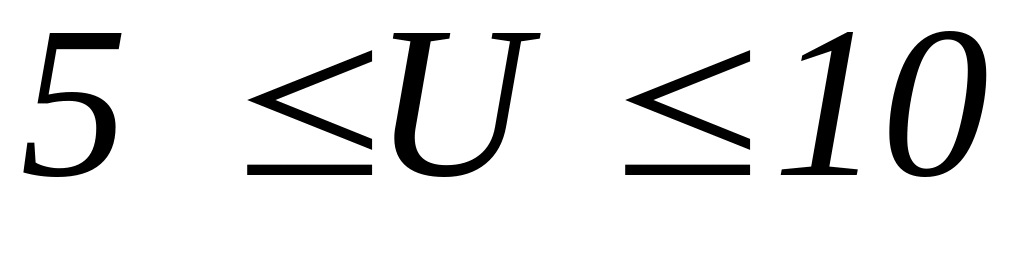 В.
В.
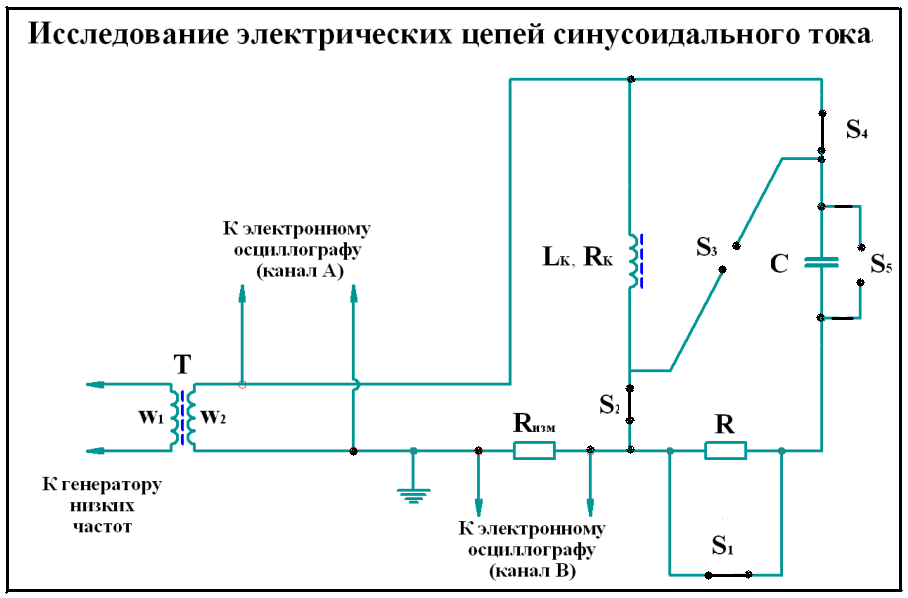
Рис. 3. Электрическая схема съемной панели для исследования резонанса токов
Используя исходные данные пункта 1 рабочего задания, рассчитать для параллельного резонансного контура:
резонансную частоту ;
волновое сопротивление ;
добротность резонансного контура
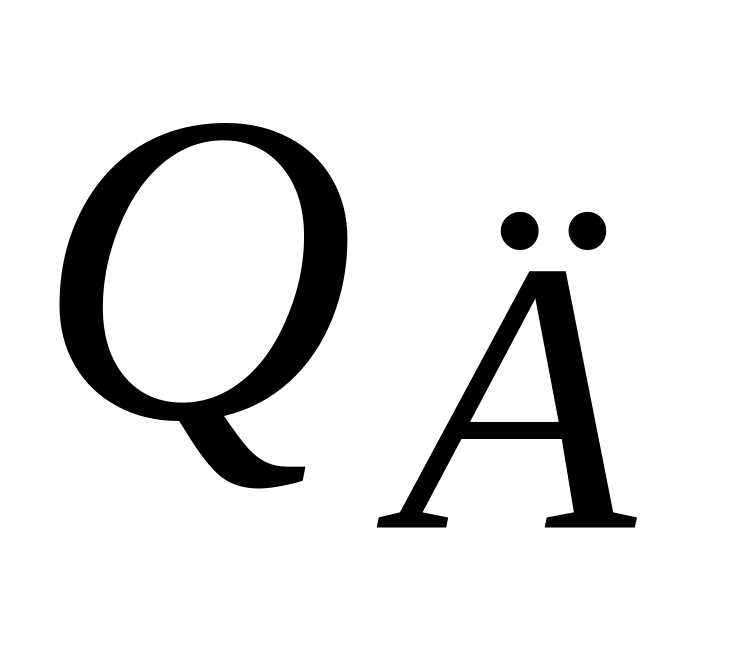 ;
;параметр затухания
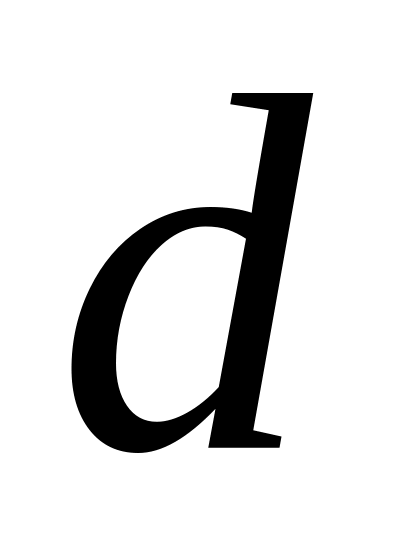 ;
;
реактивные (
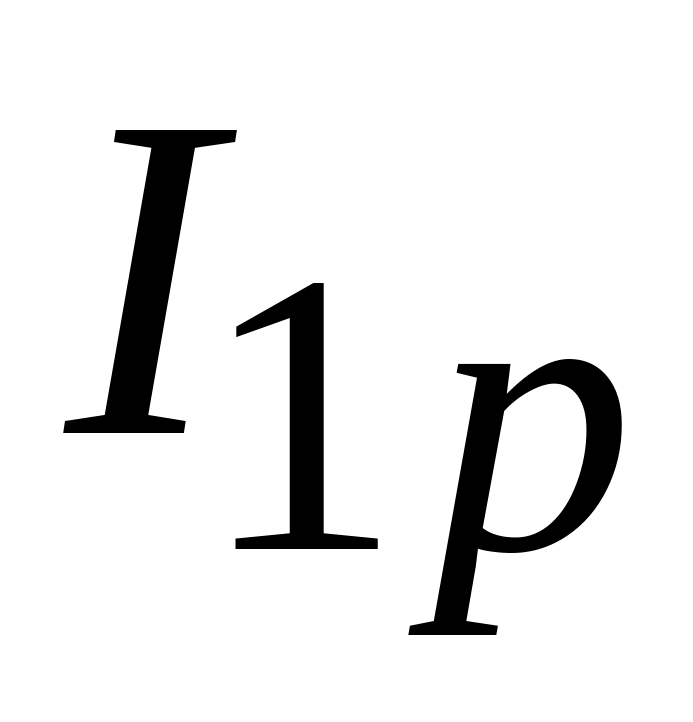 и
и
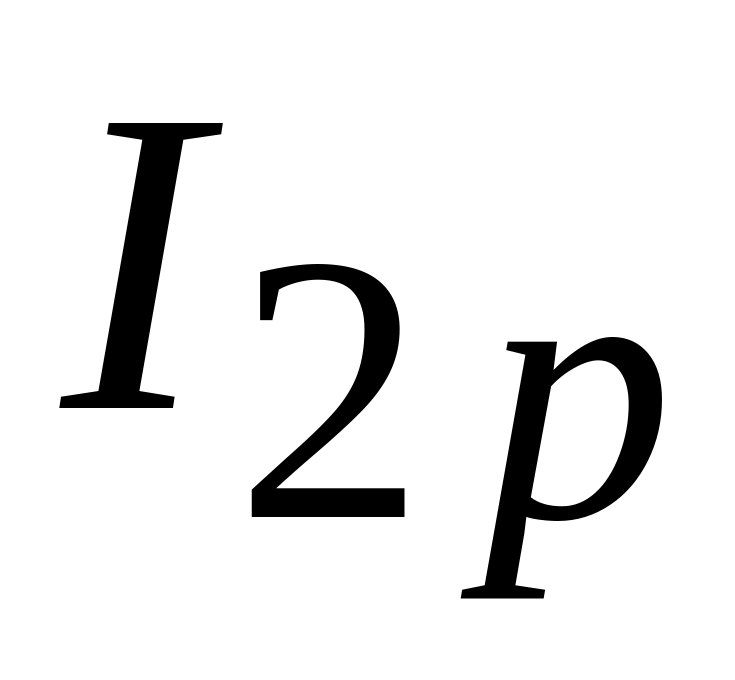 )
и активные (
)
и активные (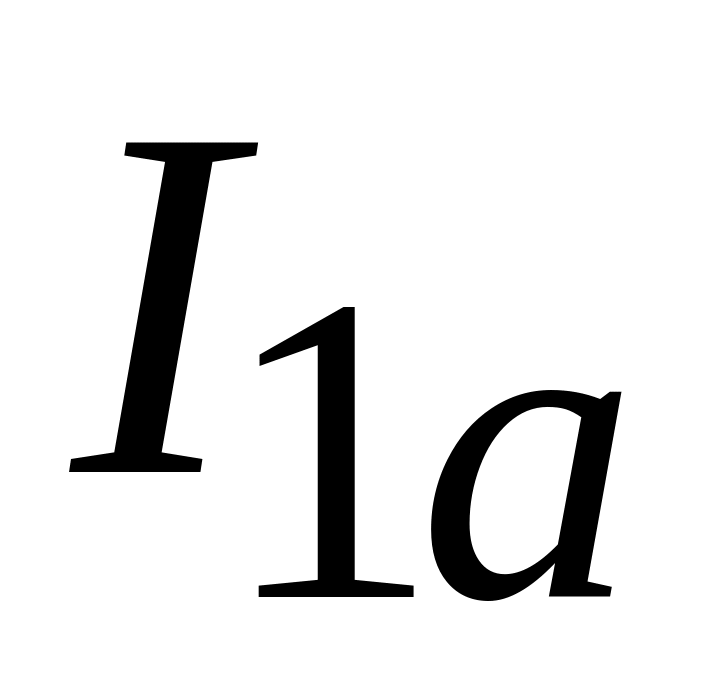 и
и
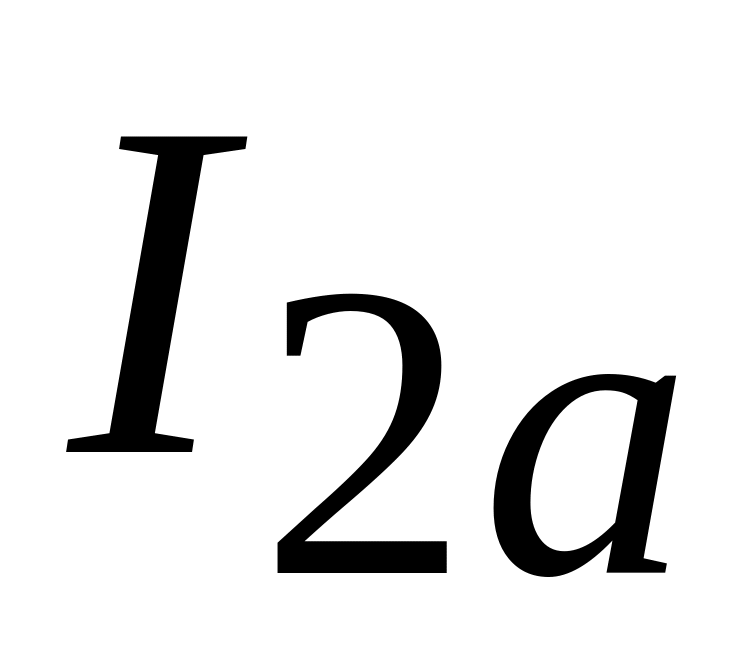 )
составляющие токов в параллельных
ветвях;
)
составляющие токов в параллельных
ветвях;токи в параллельных ветвях (
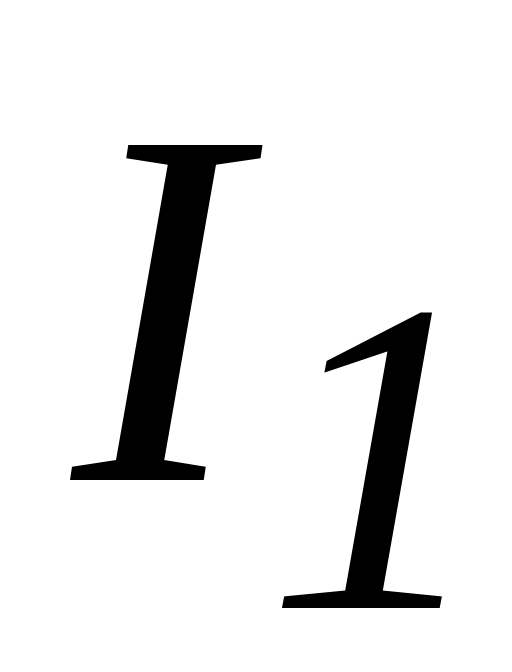 и
и
 ),
а также ток
),
а также ток
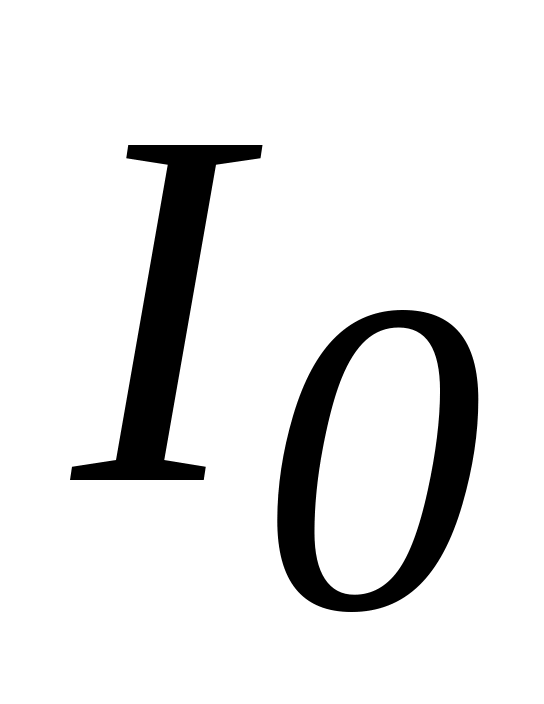 на неразветвленном участке цепи при
резонансе;
на неразветвленном участке цепи при
резонансе;добротность резонансного контура .
При выполнении расчетов по пункту 2 рабочего задания использовать следующие соотношения:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
В цепи (рис. 5), находящейся под напряжением, изменяя частоту ГНЧ с помощью ручек управления «Грубо» и «Точно» в окрестности расчетного значения , найти резонансную частоту опытным путем, так, чтобы на экране осциллографа угол сдвига фаз между напряжением на зажимах вторичной обмотки трансформатора (канал A) и напряжением (канал B) был близок нулю.
В электрической цепи (рис. 3) измерить ток , входное напряжение вольтметром PV1, токи в параллельных ветвях и амперметром PA1, последовательно подсоединяя его к участку цепи, а также угол сдвига фаз между приложенным напряжением и напряжением на сопротивлении
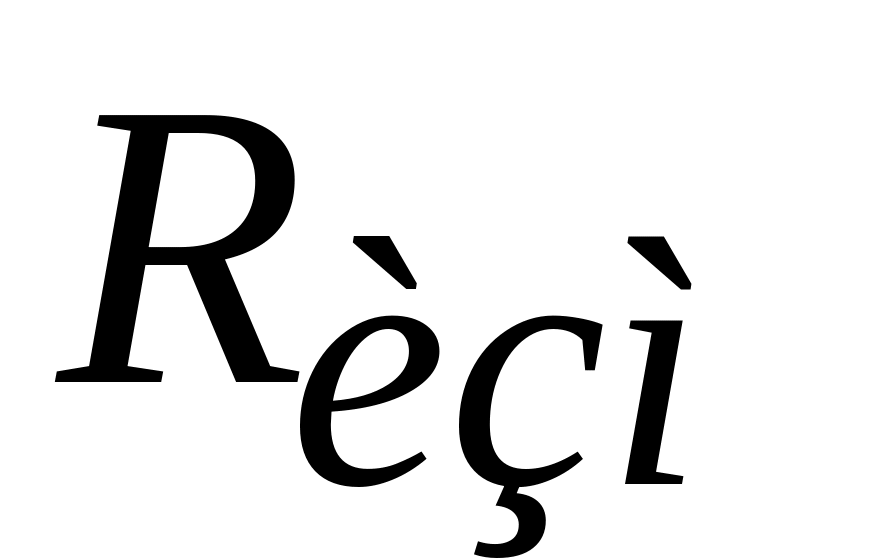 с помощью осциллографа:
с помощью осциллографа:
,
варьируя частоту ГНЧ (где = 0, 1, 2) от резонансной частоты через интервалы Гц с помощью ручек управления «Грубо» и «Точно».
Результаты измерений занести в таблицу.
Частота, Гц |
Опыт |
Расчет |
||||||||||
В |
, В |
мА |
мА |
град |
мА |
мА |
мА |
Сим |
Сим |
Сим |
Сим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица
Дополнить таблицу пункта 4 рабочего задания расчетными данными, определив ток на неразветвленном участке цепи , активную
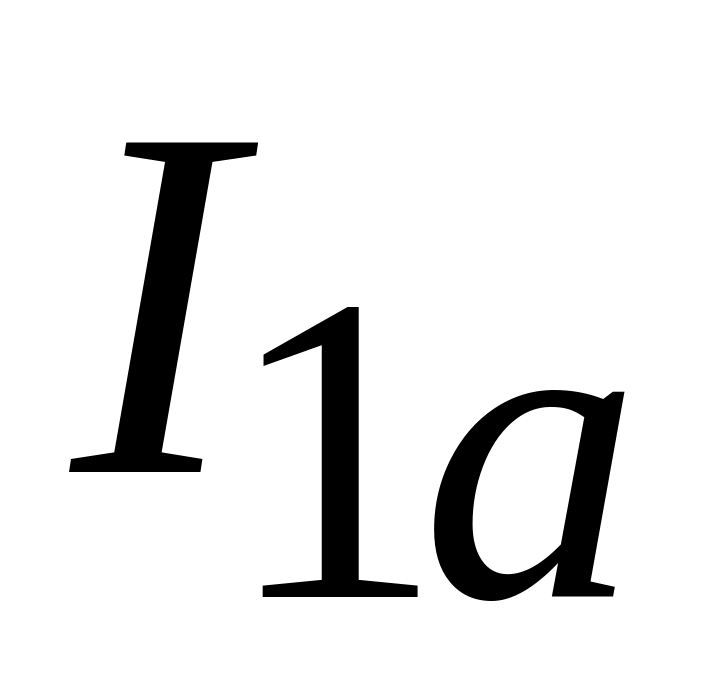 и реактивную
и реактивную
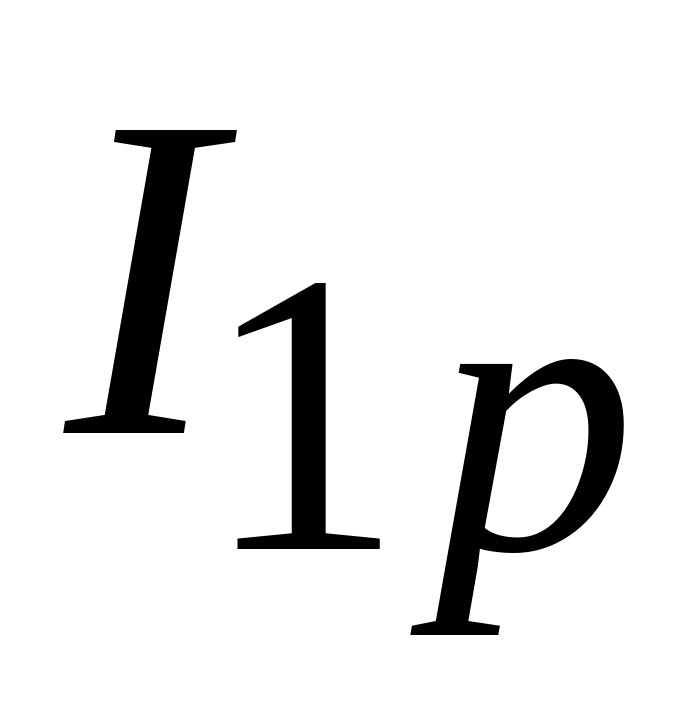 составляющие тока в катушке индуктивности,
реактивные
составляющие тока в катушке индуктивности,
реактивные
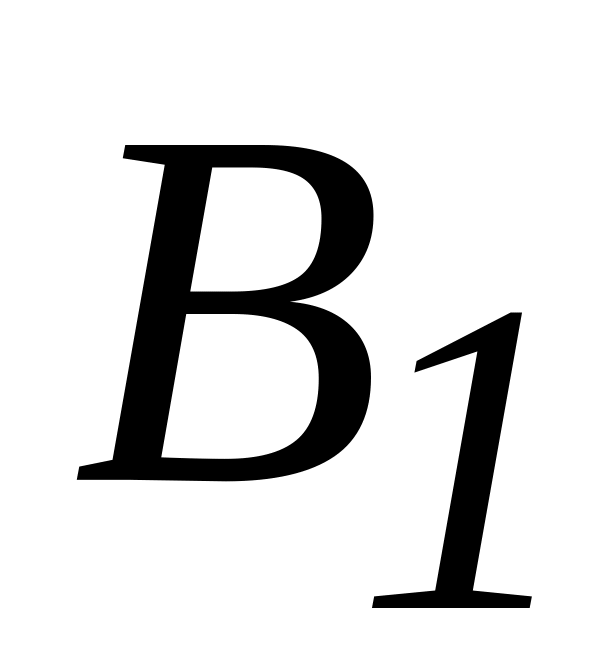 и
и
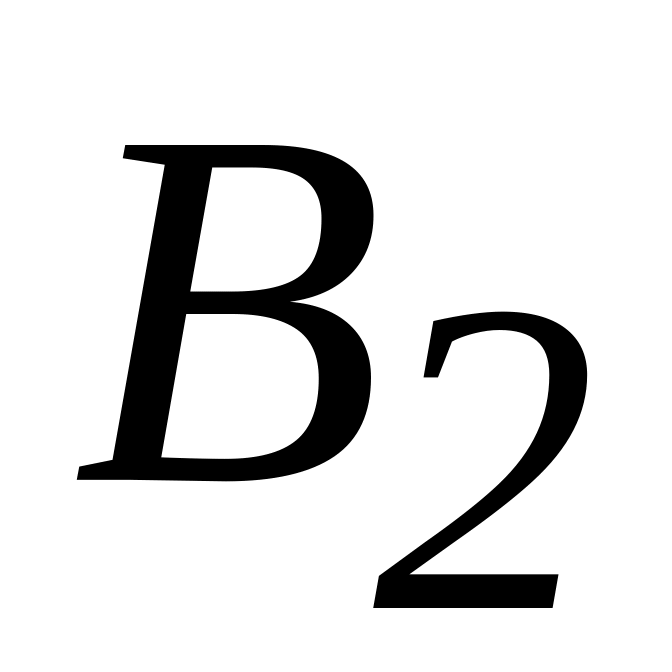 проводимости параллельных ветвей,
эквивалентные реактивную
проводимости параллельных ветвей,
эквивалентные реактивную
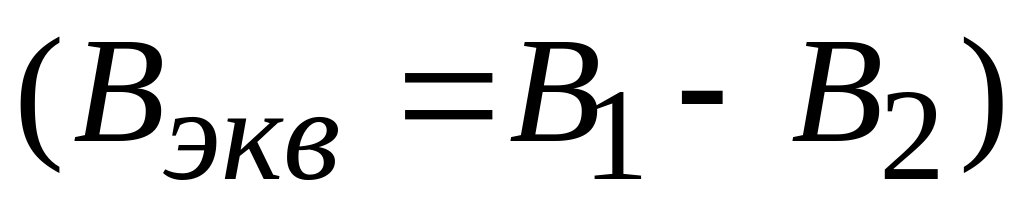 и активную
и активную
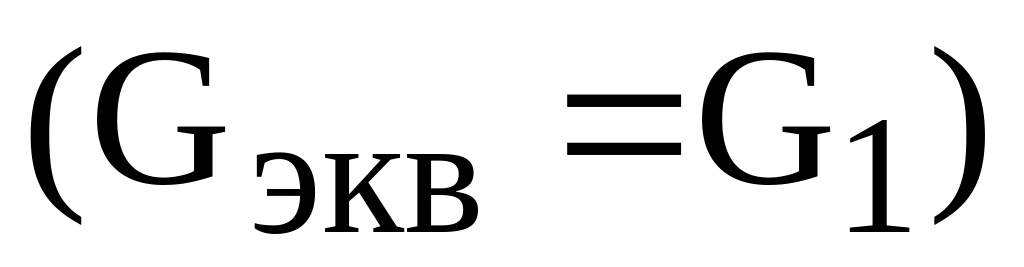 проводимости цепи.
проводимости цепи.
По данным таблицы 1 пункта 5 рабочего задания построить графики зависимости
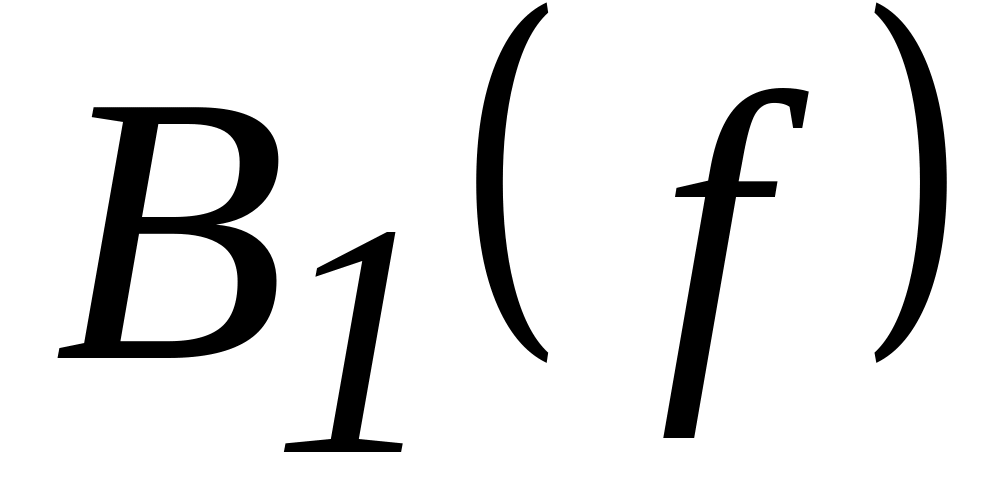 ,
,
 ,
,
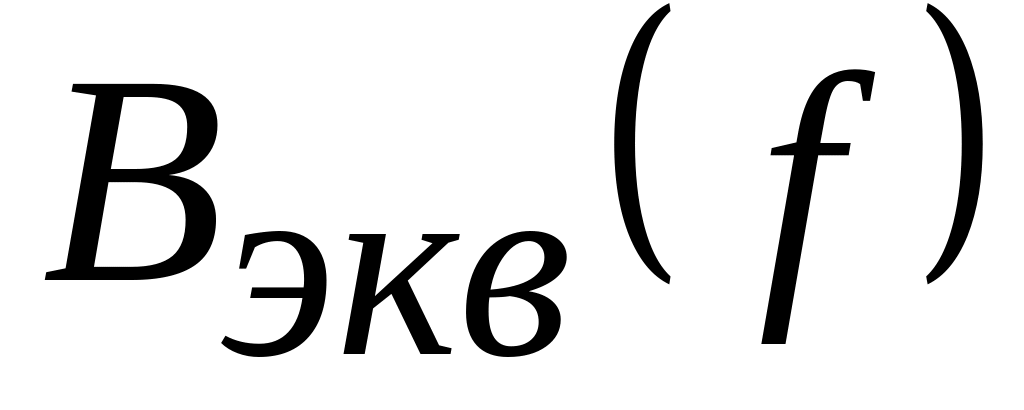 и
и
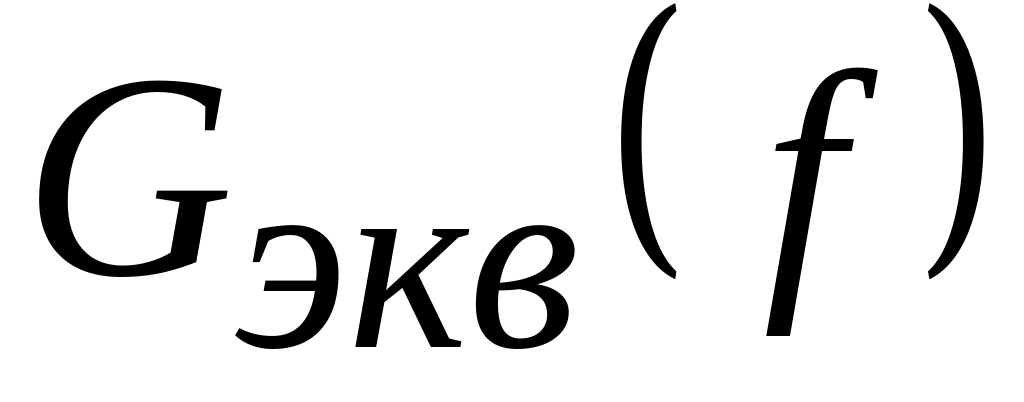 .
.
По данным таблицы 1 пункта 5 рабочего задания построить графики зависимостей
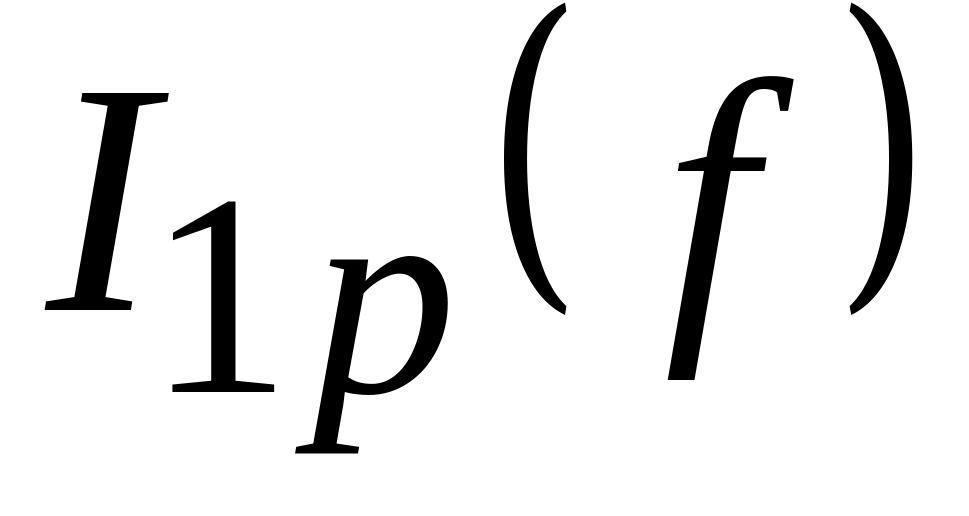 ,
,
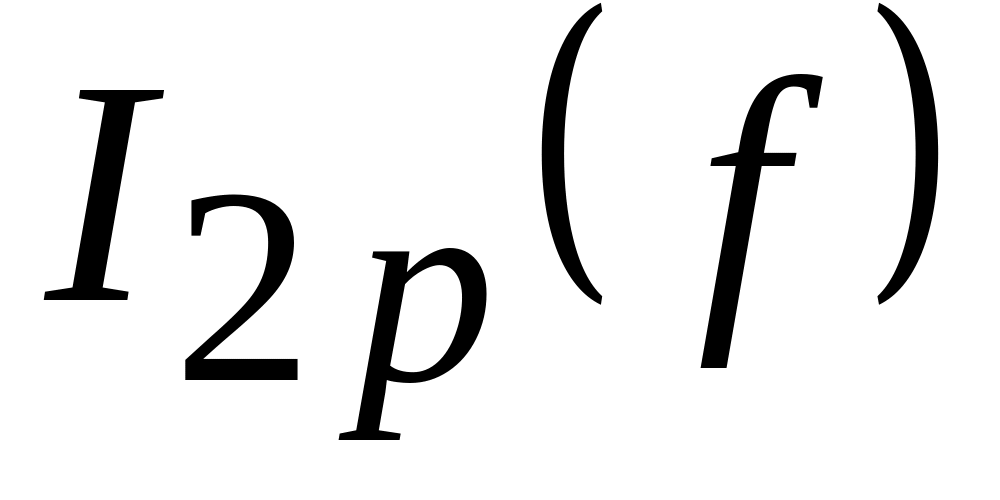 ,
,
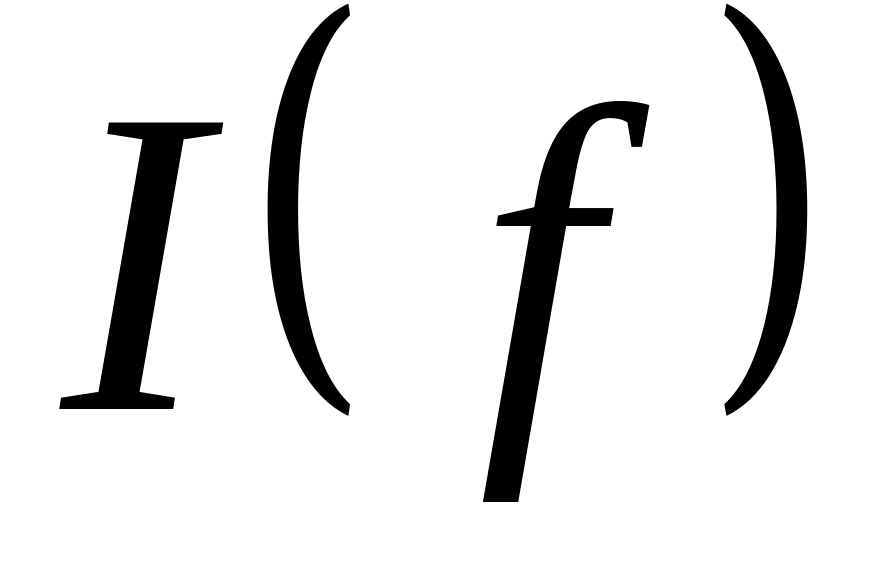 и
и
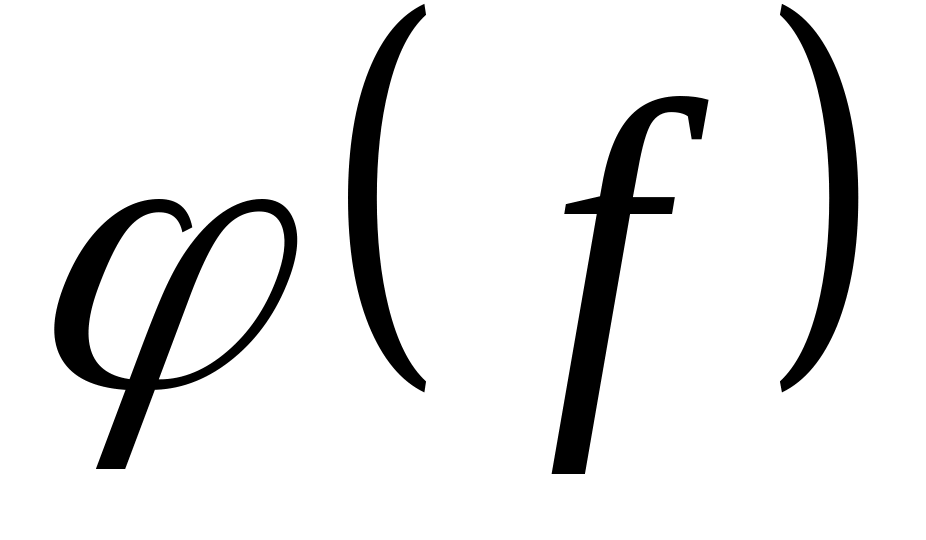 .
.
Вопросы к защите
Запишите условие резонанса токов для параллельного контура.
Что такое резонанс токов?
Применение явления резонанса токов.
Как определяется знак угла ?
Приведите формулы, по которым можно рассчитать активную, реактивную и полную проводимости параллельного контура на любой частоте, (рис. 1).
Каким образом можно экспериментально изменить резонансную частоту?
Какими способами можно определить добротность параллельного RLC – контура?
Почему входное сопротивление идеального контура бесконечно большое?
Построить векторную диаграмму токов и напряжений для идеального и реального контуров.
Содержание отчета
Ответы на вопросы домашнего задания.
Электрическая схема испытаний резонанса токов. Определение резонансной частоты опытным и расчетным путем. Сопоставление данных расчета и эксперимента.
Построение графиков, характеризующих явление резонанса токов, по данным таблицы испытаний.
Определение добротности и волнового сопротивления резонансного контура.
Выводы.
