- •Математика
- •2 Семестр Тренировочные задачи и упражнения
- •1. Дифференциальное исчисление функции одной переменной.
- •1.4 Найти предел .
- •1.19 Найти предел .
- •Найти предел .
- •1.21 Найти предел .
- •2. Интегрирование функции одной переменной.
- •5. Дифференциальные уравнения
- •Разделяем переменные:
- •6. Функции нескольких переменных.
6. Функции нескольких переменных.
6.1
Найти частные производные функции
![]()
Решение:
![]()
![]()
6.2
Найти частные производные второго
порядка функции
![]()
Решение:
Так как
![]() ,
то
,
то
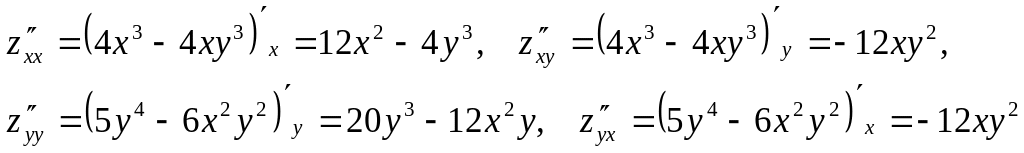
![]()
![]()
6.3 Найти полный
дифференциал функции
![]() .
.
Решение:
![]()
![]()
![]()
6.4 Найти полный
дифференциал функции
![]()
Решение:
![]()
![]()
![]()
Найти уравнения касательной плоскости и нормали к поверхности
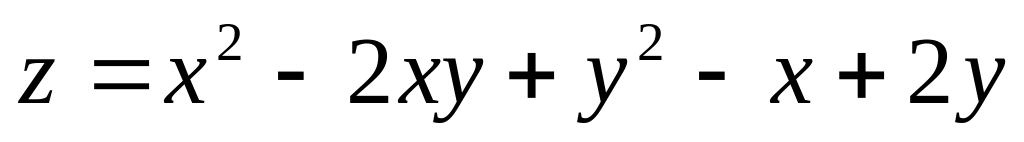 в точке М(1, 1, 1).
в точке М(1, 1, 1).
Решение:
![]()
![]()
Уравнение касательной плоскости:
![]()
Уравнение
нормали:![]()
6.6 Вычислить
приближенно значение
![]() ,
исходя из значения функции
,
исходя из значения функции
![]() при x = 1, y =
2, z = 1.
при x = 1, y =
2, z = 1.
Решение: Из заданного выражения определим x = 1,04 – 1 = 0,04, y = 1,99 – 2 = -0,01,
z = 1,02 – 1 = 0,02.
Найдем
значение функции u(x,
y, z) =
![]()
Находим частные
производные:
![]()
![]()
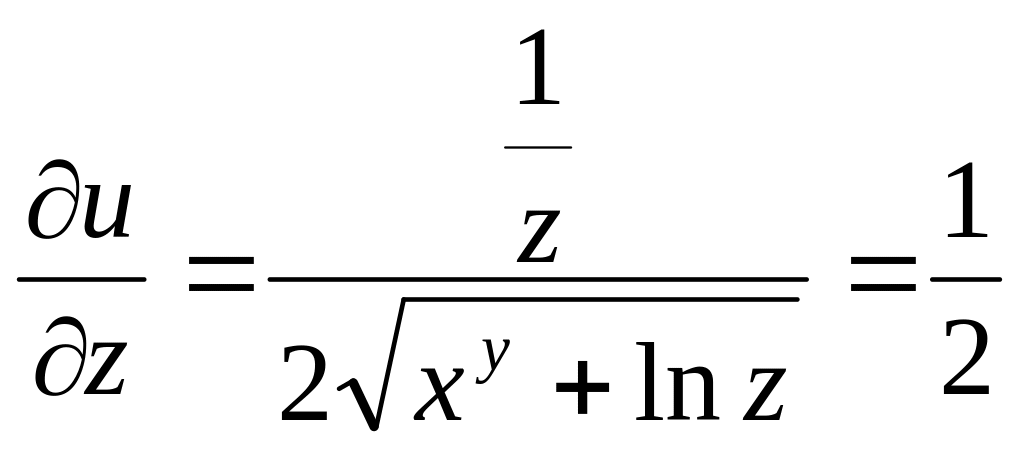
Полный дифференциал функции u равен:
![]()
![]()
Точное значение этого выражения: 1,049275225687319176.
6.7 Найти экстремум функции f(x, y) = xy, если уравнение связи: 2x + 3y – 5 = 0
Решение:
![]()
![]()
![]()
![]()
Таким образом, функция
имеет экстремум в точке
![]() .
.
6.8 Вычислить
производную функции z =
x2 + y2x
в точке А(1, 2) по направлению вектора
![]() .
В (3, 0). Вычислить градиент этой функции
в точке А.
.
В (3, 0). Вычислить градиент этой функции
в точке А.
Решение. Прежде всего необходимо определить координаты вектора .
=(3-1;
0-2) = (2; -2) = 2![]() .
.
Далее
определяем модуль этого вектора:![]() =
=![]()
Находим частные производные функции z в общем виде:
![]()
Значения
этих величин в точке А :
![]()
Тогда
градиент функции имеет вид:
![]()
Для нахождения
направляющих косинусов вектора
производим следующие преобразования:![]() =
=
![]()
За величину принимается орт вектора .
Отсюда получаем значения направляющих косинусов вектора :
cos
=
![]() ;
cos
= -
;
cos
= -
Окончательно получаем:
![]() - значение производной заданной функции
по направлению вектора
.
- значение производной заданной функции
по направлению вектора
.
6.9. Исследовать на экстремум функцию
![]() .
.
Решение. Область определения
![]() — вся числовая плоскость
— вся числовая плоскость
![]() ,
,
![]() дифференцируема в каждой точке
дифференцируема в каждой точке
![]() .
.
Определим стационарные точки .
![]()
![]()
![]()
Отсюда
![]()
Получили
три стационарные точки:
![]()
Эти точки исследуем на достаточность условий экстремума. Сначала определим отдельно
![]()
А теперь
для каждой точки вычислим соответствующие
![]() ,
определим знаки величин
,
определим знаки величин
![]() и
и
![]() .
.
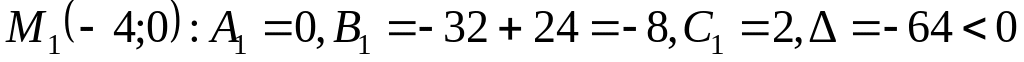 ,
т.е.
,
т.е.
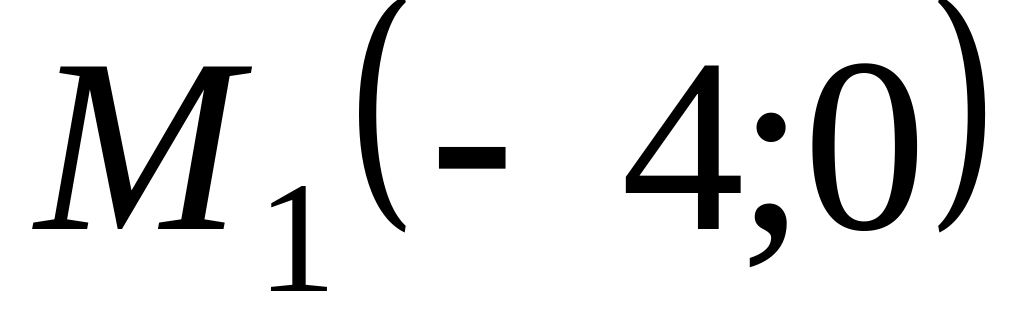 не является точкой экстремума.
не является точкой экстремума.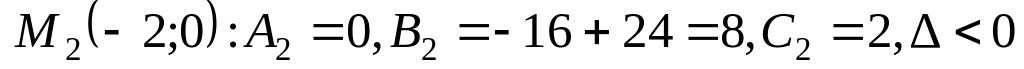 т.е.
т.е.
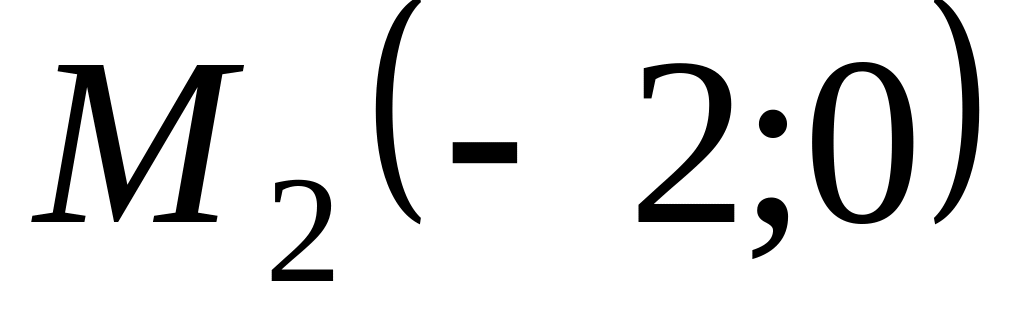 не является точкой экстремума.
не является точкой экстремума.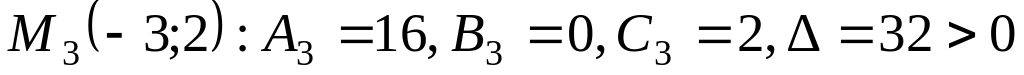 .
При этом
.
При этом
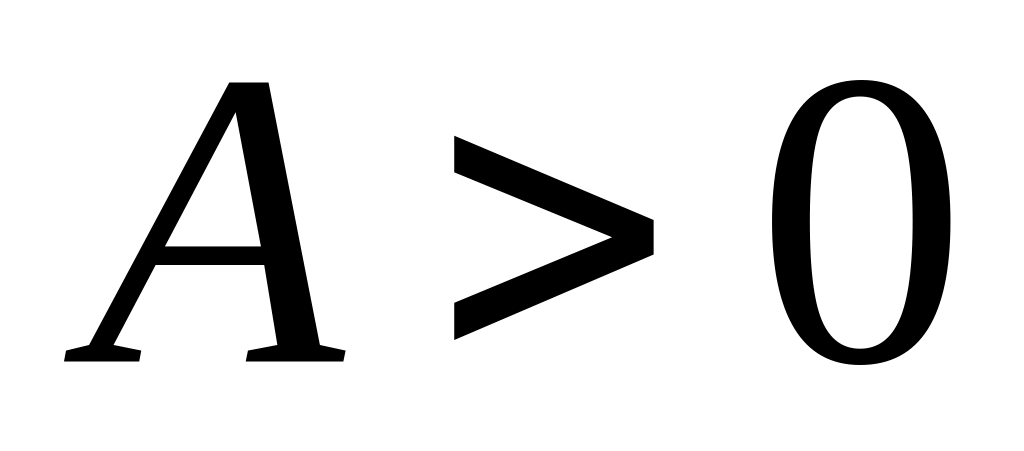 .
Вывод:
.
Вывод:
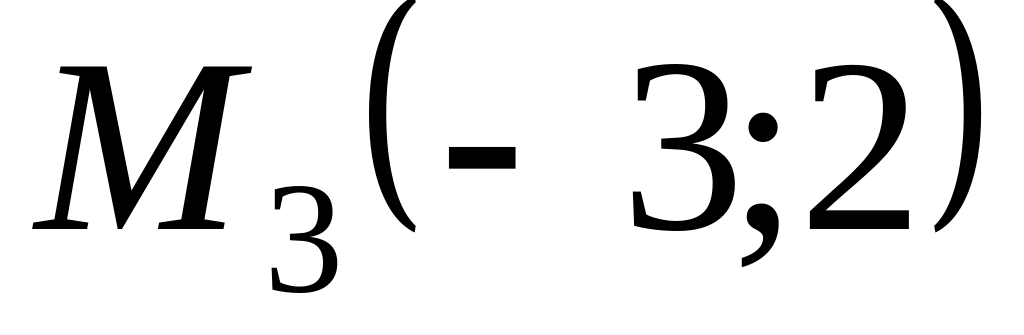 — точка локального минимума функции
с
— точка локального минимума функции
с
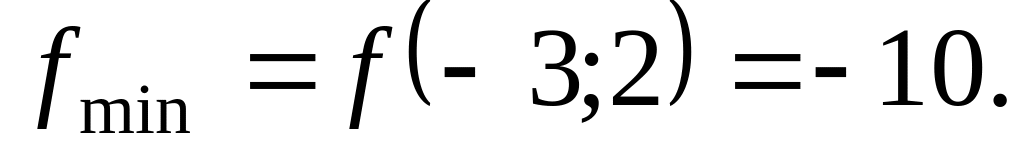
Ответ:
![]()
6.10. Найти
наибольшее и наименьшее значения функции
![]() в замкнутой области, ограниченной
линиями:
в замкнутой области, ограниченной
линиями:
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Решение.
|
Находим все критические точки:
Решением системы являются точки
|
Ни одна
из найденных точек не принадлежит
области
![]() .
.
Исследуем функцию
 на границе области, состоящей из участков
на границе области, состоящей из участков
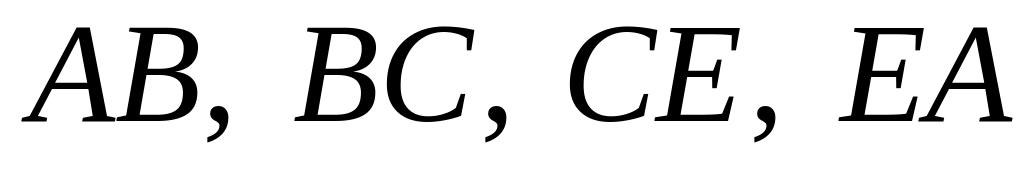 .
.
На
участке
![]() где
где
![]() ,
,
![]() .
Значения функции
.
Значения функции
![]() .
.
На
участке
![]() ,
,
![]() ,
,
![]() .
Значения функции
.
Значения функции
![]() .
.
На
участке
![]() ,
,
![]() .
Значения функции
.
Значения функции
![]() .
.
На
участке
![]() ,
,
,
,
![]() .
Значения функции
.
Значения функции
![]() .
.
Сравнивая полученные результаты, имеем:
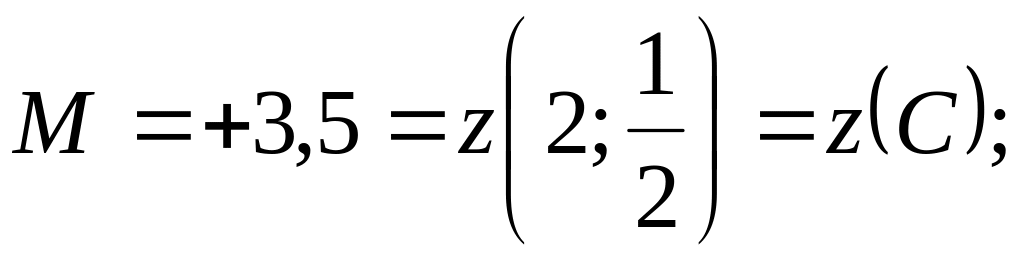
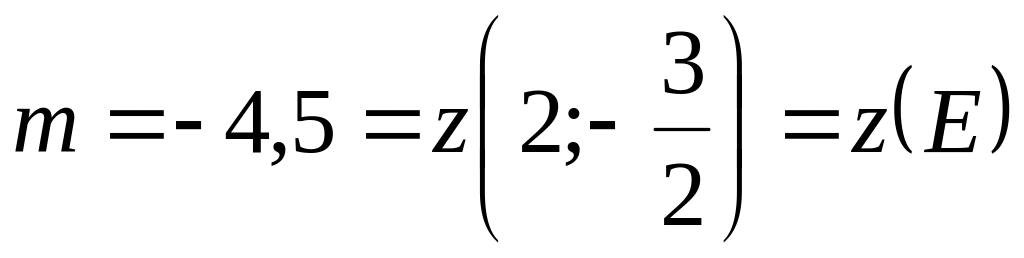 .
.
6.11. Дана
система точек, координаты которых
указаны в таблице, число точек
![]() .
Требуется построить прямую с уравнением
.
Требуется построить прямую с уравнением
![]() ,
чтобы она отличалась как можно меньше
от данной системы точек в смысле
наименьших квадратов.
,
чтобы она отличалась как можно меньше
от данной системы точек в смысле
наименьших квадратов.
X |
-1 |
0 |
1 |
2 |
3 |
4 |
Y |
0 |
2 |
3 |
3,5 |
3 |
4,5 |
Для
того, чтобы построить прямую, «сглаживающую»
данные точки (они не лежат на одной
прямой). Для этого достаточно решить
систему уравнений
![]() .
Для удобства расчетов строим рабочую
таблицу
.
Для удобства расчетов строим рабочую
таблицу
№ |
|
|
|
|
|
|
|
1 2 3 4 5 6 |
-1 0 1 2 3 4
|
0 2 3 3,5 3 4,5 |
1 0 1 4 9 16 |
0 0 3 7 9 18 |
0,81 1,55 2,29 3,03 3,77 4,51 |
0,81 -0,45 -0,71 -0,47 0,77 0,01 |
0,6561 0,2025 0,5041 0,2209 0,5929 0,001 |
|
9
|
16
|
31
|
37
|
|
|
2,1766 |
Первый
столбец обозначает номер по порядку
записи точек. Из сумм столбцов при
![]() составляются коэффициенты системы для
определения параметров
составляются коэффициенты системы для
определения параметров
![]() и
и
![]() прямой
прямой
![]() .
Система имеет вид:
.
Система имеет вид:
![]()
Решим ее методом определителей (Крамера):
![]()
![]()
![]()
![]()
Искомое
уравнение
![]() .
.