5. Дифференциальные уравнения

5.1 Найти общее решение дифференциального уравнения .

Решение: Общее решение дифференциального уравнения ищется с помощью интегрирования левой и правой частей уравнения, которое предварительно преобразовано следующим образом:

Теперь интегрируем:

- это общее решение исходного дифференциального уравнения.

Если заданы начальные условия у(х₀) = у_{0 ,} допустим x₀ = 1; y₀ = 2, тогда имеем

При подстановке полученного значения постоянной в общее решение получаем частное решение при заданных начальных условиях (решение задачи Коши):

5.2 Найти общее решение дифференциального уравнения:

Решение: Найти особое решение, если оно существует.

Данное дифференциальное уравнение имеет также особое решение у = 0. Это решение невозможно получить из общего, однако при подстановке в исходное уравнение получаем тождество. Мнение, что решение y = 0 можно получить из общего решения при С₁ = 0 ошибочно, ведь C₁ = e^C  0.

5.3 Найти общее решение дифференциального уравнения:

Решение:

Интеграл, стоящий в левой части, берется по частям:

это есть общий интеграл исходного дифференциального уравнения, т.к. искомая функция и не выражена через независимую переменную.

5.4 Найти решение дифференциального уравнения при условии у(2) = 1.

Решение:

при у(2) = 1 получаем

Итого: или - частное решение;

5.5 Решить уравнение .

Решение:

Получаем общий интеграл:

5.6 Решить уравнение .

Решение: Введем вспомогательную функцию u.

.

Отметим, что введенная нами функция u всегда положительна, т.к. в противном случае теряет смысл исходное дифференциальное уравнение, содержащее .

Подставляем в исходное уравнение:

Разделяем переменные:

Интегрируя, получаем:

Переходя от вспомогательной функции обратно к функции у, получаем общее решение:

5.7 Решить уравнение

Решение: Получаем

Находим значение определителя .

Решаем систему уравнений

Применяем подстановку в исходное уравнение:

Заменяем переменную при подстановке в выражение, записанное выше, имеем:

Разделяем переменные:

Переходим теперь к первоначальной функции у и переменной х.

Итого, выражение является общим интегралом исходного дифференциального уравнения.

5.8 Решить уравнение

Решение: Полагаем , тогда , т. е. . Сначала решаем уравнение Теперь решаем уравнение , т.е. . Итак, общее решение данного уравнения есть , т.е.

5.9 Решить уравнение .

Решение: Полагаем , тогда , т. е. . Сначала решаем уравнение Теперь решаем уравнение , т.е. . Итак, общее решение данного уравнения есть

5.10 Решить уравнение

Решение: Проверим условие

Условие выполняется, следовательно, исходное дифференциальное уравнение является уравнением в полных дифференциалах.

Определим функцию u.

;

Итого,

Находим общий интеграл исходного дифференциального уравнения:

5.11 Решить уравнение с начальными условиями x₀ = 0; y₀ = 1;

Решение:

Подставим начальные условия:

Получаем частное решение (решение задачи Коши): .

5.12 Найти общее решение уравнения .

Решение: Применяем подстановку

Произведя обратную замену, получаем:

Общее решение исходного дифференциального уравнения:

5.13 Найти общее решение уравнения

Решение: Замена переменной:

1)

Для решения полученного дифференциального уравнения произведем замену переменной:

С учетом того, что , получаем:

Общий интеграл имеет вид:

2)

Таким образом, получили два общих решения.

5.14 Решить уравнение .

Решение: Составим характеристическое уравнение:

Общее решение имеет вид:

5.15 Решить уравнение

Решение: Это линейное однородное дифференциальное уравнение с переменными коэффициентами второго порядка. Для нахождения общего решения необходимо отыскать какое - либо частное решение.

Таким частным решением будет являться функция

Исходное дифференциальное уравнение можно преобразовать:

Общее решение имеет вид:

Окончательно:

5.16 Решить уравнение

Решение: Характеристическое уравнение:

Общее решение:

5.17 Решить уравнение

Решение: Характеристическое уравнение:

Общее решение:

5.18 Решить уравнение

Решение: Характеристическое уравнение:

Общее решение:

5.19 Решить уравнение

Решение: Характеристическое уравнение:

Общее решение:

5.20 Решить уравнение

Решение: Решаем линейное однородное уравнение

Решение неоднородного уравнения будет иметь вид:

Составляем систему уравнений:

Решим эту систему:

Из соотношения найдем функцию А(х).

Теперь находим В(х).

Подставляем полученные значения в формулу общего решения неоднородного уравнения:

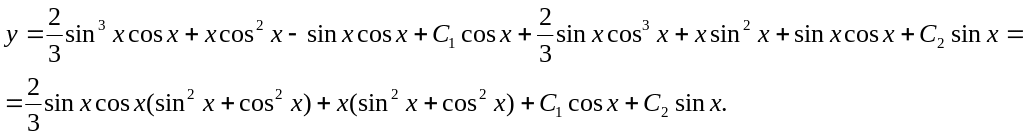Окончательный ответ:

5.21 Решить уравнение .

Решение: Решим соответствующее однородное уравнение:

Теперь найдем частное решение исходного неоднородного уравнения.

Сопоставим правую часть уравнения с видом правой части

Частное решение ищем в виде: , где

Т.е.

Теперь определим неизвестные коэффициенты А и В.

Подставим частное решение в общем виде в исходное неоднородное дифференциальное уравнение.

Итого, частное решение:

Тогда общее решение линейного неоднородного дифференциального уравнения:

5.22 Решить уравнение

Решение:

Правую часть дифференциального уравнения представим в виде суммы двух функций f₁(x) + f₂(x) = x + (-sinx).

Составим и решим характеристическое уравнение:

1. Для функции f₁(x) = х ( 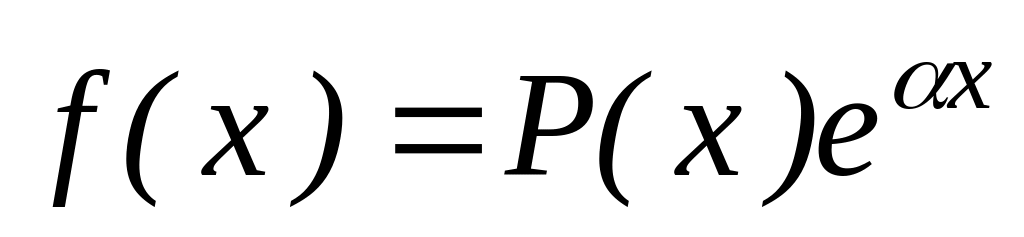)решение ищем в виде .

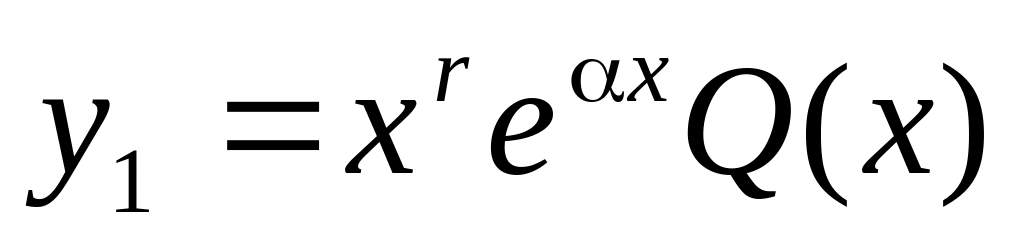Получаем: Т.е.

Итого:

2. Для функции f₂(x) = -sinx ( 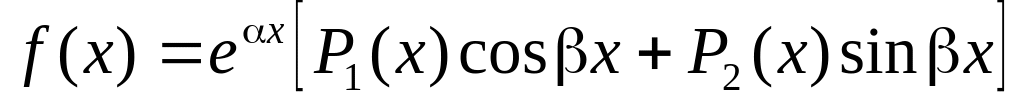) решение ищем в виде: .

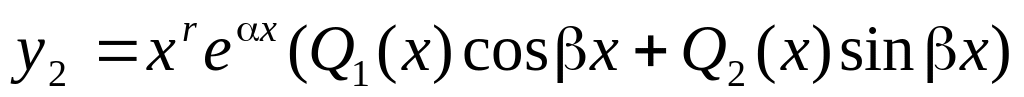Анализируя функцию f₂(x), получаем:

Таким образом,

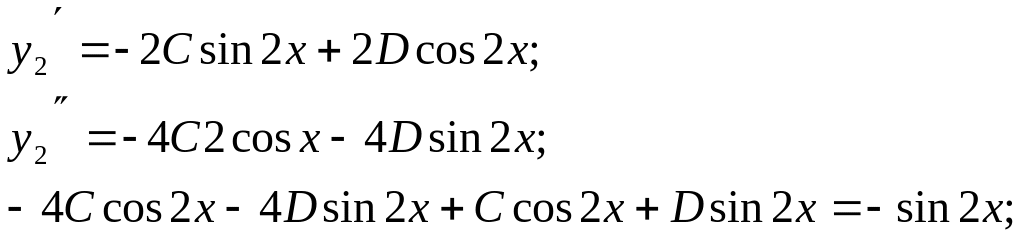
Итого:

Т.е. искомое частное решение имеет вид:

Общее решение неоднородного дифференциального уравнения:

5.23 Решить уравнение

Решение:

Составим характеристическое уравнение для соответствующего линейного однородного дифференциального уравнения:

Общее решение однородного уравнения:

Теперь найдем частное решение неоднородного уравнения в виде:

Воспользуемся методом неопределенных коэффициентов.

Подставляя в исходное уравнение, получаем:

Частное решение имеет вид:

Общее решение линейного неоднородного уравнения:

5.24 Решить уравнение

Решение:

Характеристическое уравнение:

Общее решение однородного уравнения:

Частное решение неоднородного уравнения: .

Находим производные и подставляем их в исходное неоднородное уравнение:

Получаем общее решение неоднородного дифференциального уравнения:

5.25 Найти общее решение системы уравнений:

Решение: Составим характеристическое уравнение:

Решим систему уравнений:

Для k₁:

Полагая (принимается любое значение), получаем:

Для k₂:

Полагая (принимается любое значение), получаем:

Общее решение системы:

5.26 Найти решение системы уравнений

Решение: Эта система дифференциальных уравнений не относится к рассмотренному выше типу, т.к. не является однородным (в уравнение входит независимая переменная х).

Для решения продифференцируем первое уравнение по х. Получаем:

Заменяя значение z’ из второго уравнения получаем: .

С учетом первого уравнения, получаем:

Решаем полученное дифференциальное уравнение второго порядка.

Общее решение однородного уравнения:

Теперь находим частное решение неоднородного дифференциального уравнения по формуле

Общее решение неоднородного уравнения:

Подставив полученное значение в первое уравнение системы, получаем:

5.27 Найти решение системы уравнений:

Решение: Составим характеристическое уравнение:

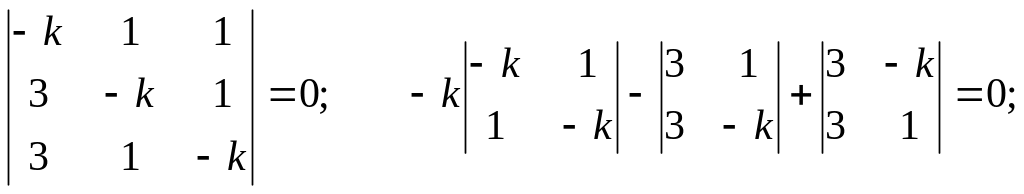
1. k = -1.

Если принять  = 1, то решения в этом случае получаем:

2. k₂ = -2.

Если принять  = 1, то получаем:

3. k₃ = 3.

Если принять  = 3, то получаем:

Общее решение имеет вид:

5.28 Методом Эйлера найти значение решения дифференциального уравнения для которого y(1)=1, в пяти точках отрезка [1;1,5], приняв h=0,1.

По формулам

находим точки Значение искомой функции y=y(x), удовлетворяющей условию данной задачи Коши, вычисляем по формуле

(k = 0, 1, 2, …, n ).

Результаты вычислений занесены в таблицу 1.

Таблица 1

k
0	1,0000	1,0	1,0	1,0000	0,1000	1,1000
1	1,1000	1,1	2,2	1,1000	0,1100	1,2100
2	1,2100	1,2	2,4	1,9000	0,1190	1,3290
3	1,3290	1,3	2,6	1,2710	0,1271	1,4561
4	1,4561	1,4	2,8	1,3439	0,1344	1,5905
5	1,5905	1,5	3,0	1,4095	0,1410	1,7315