1.19 Найти предел .
Решение. Как видно, при попытке непосредственного вычисления предела получается неопределенность вида . Функции, входящие в числитель и знаменатель дроби удовлетворяют требованиям теоремы Лопиталя.
f(x)
= 2x +
;
g(x)
= ex;
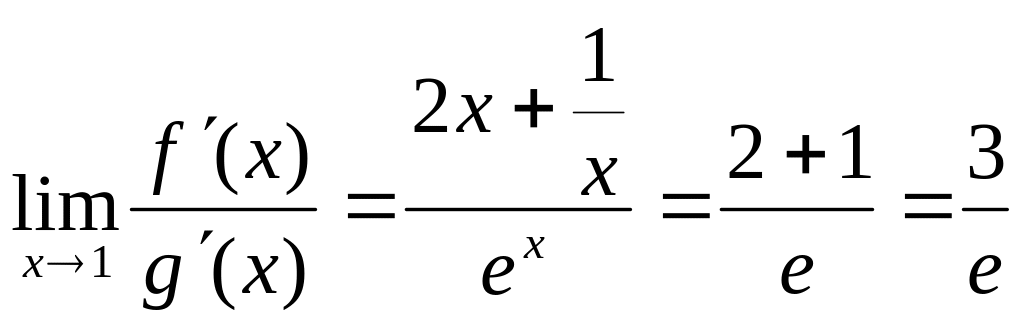
Найти предел .
Решение.
;
;
- опять получилась неопределенность.
Применим правило Лопиталя еще раз.
;
;
- применяем правило Лопиталя еще раз.
;
;
1.21 Найти предел .
Решение. Здесь y = xx, lny = xlnx.
Тогда
.
Следовательно
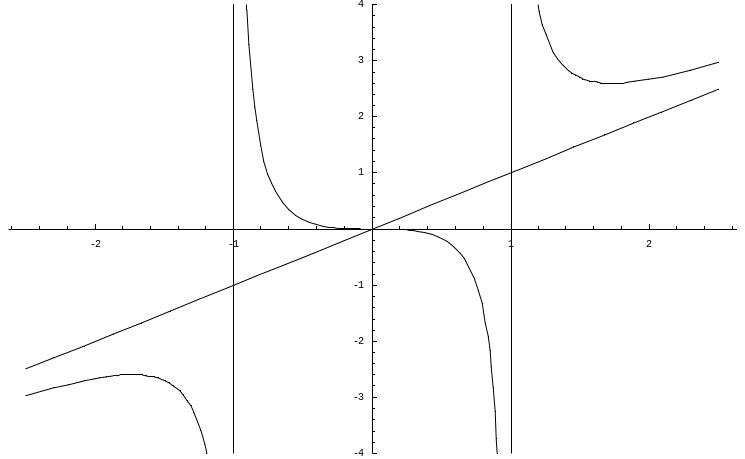
1.22 Исследовать функцию
и
построить ее график.
Решение. Находим область существования функции. Очевидно, что областью определения функции является область (-; -1) (-1; 1) (1; ).
В свою очередь, видно, что прямые х = 1, х = -1 являются вертикальными асимптотами кривой.
Областью значений данной функции является интервал (-; ).
Точками разрыва функции являются точки х = 1, х = -1.
Находим критические точки.
Найдем производную функции
Критические
точки: x = 0; x
= -
;
x =
;
x = -1; x = 1.
Найдем вторую производную функции
.
Определим выпуклость и вогнутость кривой на промежутках.
- < x < - , y < 0, кривая выпуклая
- < x < -1, y < 0, кривая выпуклая
-1 < x < 0, y > 0, кривая вогнутая
0 < x < 1, y < 0, кривая выпуклая
1 < x < , y > 0, кривая вогнутая
< x < , y > 0, кривая вогнутая
Находим промежутки возрастания и убывания функции. Для этого определяем знаки производной функции на промежутках.
- < x < - , y > 0, функция возрастает
- < x < -1, y < 0, функция убывает
-1 < x < 0, y < 0, функция убывает
0 < x < 1, y < 0, функция убывает
1 < x < , y < 0, функция убывает
< x < , y > 0, функция возрастает
Видно, что точка х = - является точкой максимума, а точка х = является точкой минимума. Значения функции в этих точках равны соответственно 3 /2 и -3 /2.
Про вертикальные асимптоты было уже сказано выше. Теперь найдем наклонные асимптоты.
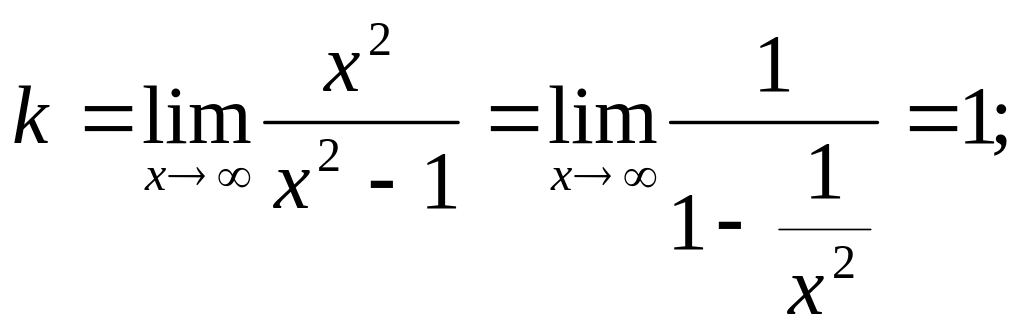
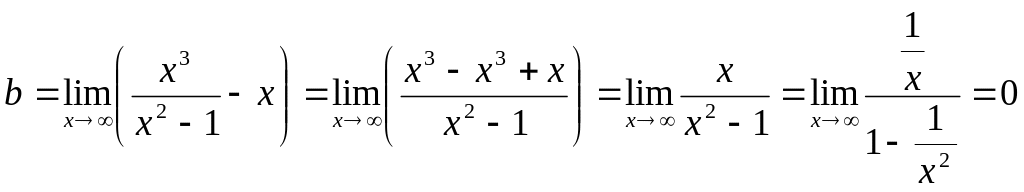
Итого, уравнение наклонной асимптоты – y = x.
Построим график функции:
1.23.Найти кривизну дуги
плоской кривой
,
изображенной на рис.
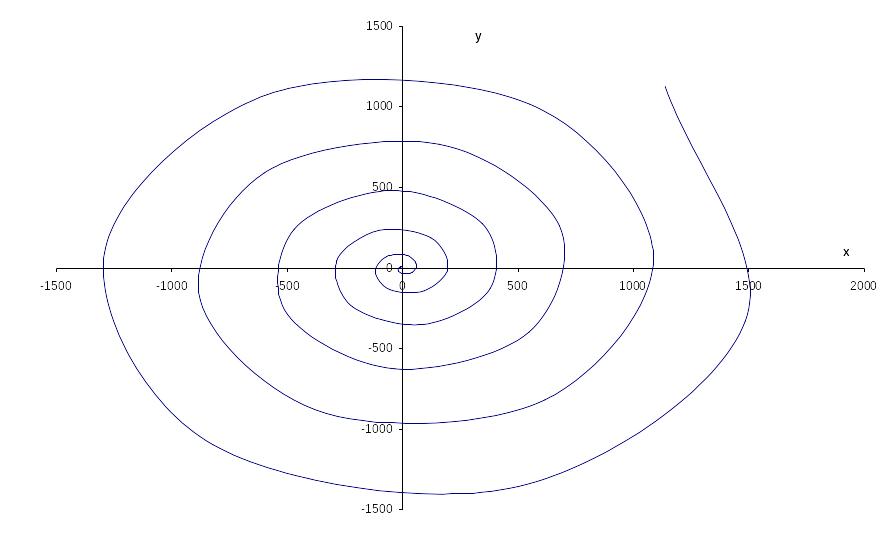
Решение. Найдем производные x, y первого и второго порядков по переменной t:
Подставив найденные производные в формулу
получим кривизну кривой равную:
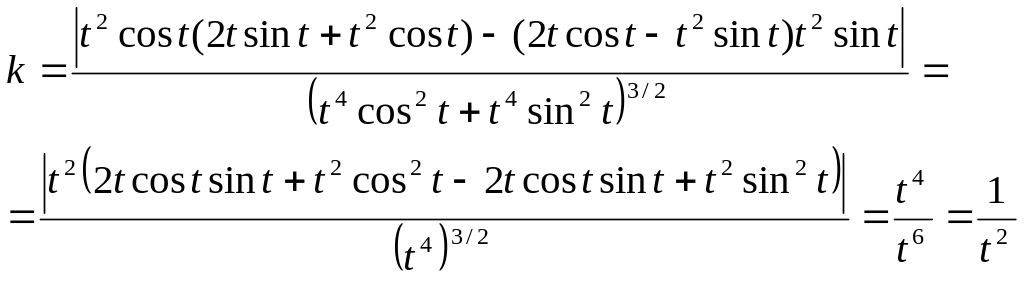
1.24.Найти кривизну и радиус кривизны
линии
в точке
.
Решение. Используем формулу для
кривизны
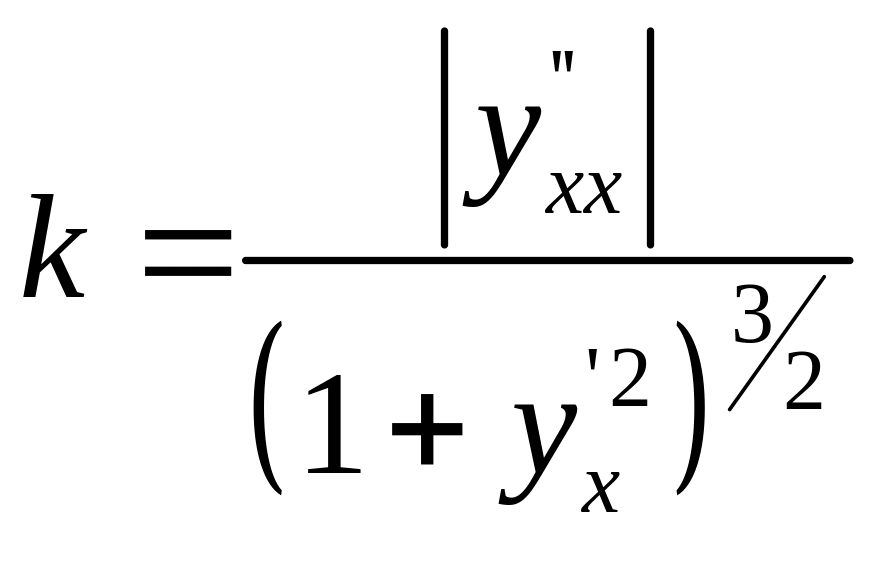и радиуса
.
Вычислив первую и вторую производные
и подставив туда значения для х, получим
,
.
1.25. Найти область определения функции
.
Решение. Для нахождения D(y ) необходимо решить систему неравенств
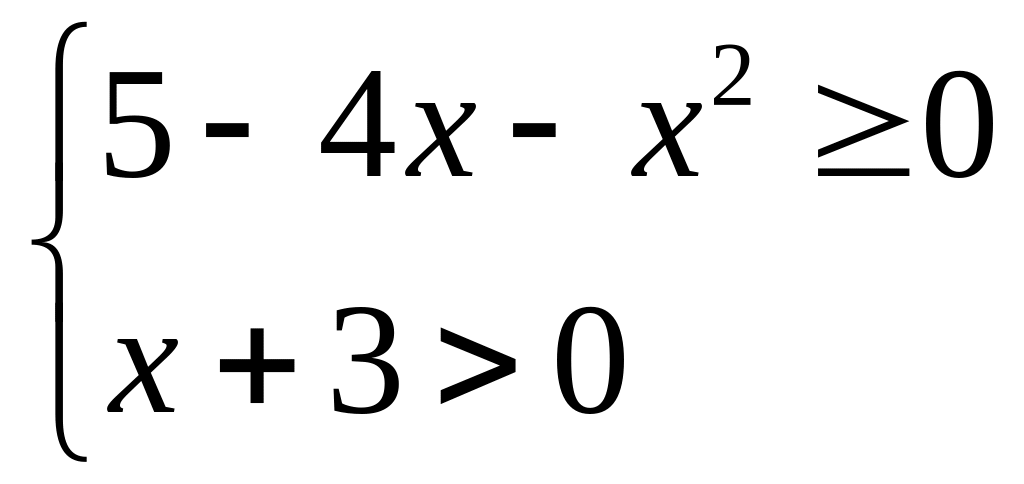
В результате получаем
.
2. Интегрирование функции одной переменной.
2.1
Вычислить интеграл
2.2
Вычислить интеграл
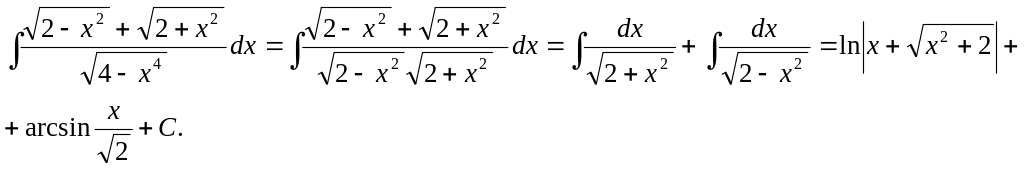
2.3 Вычислить интеграл
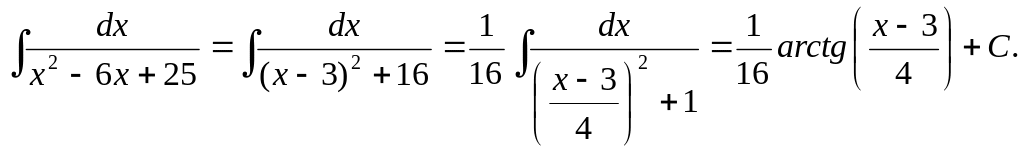
2.4 Найти
неопределенный интеграл
.
Решение. Сделаем замену t = sinx, dt = cosxdt.
2.5
Вычислить интеграл
Решение.
Замена
Получаем:
2.6
2.7 Вычислить интеграл
2.8
Вычислить интеграл
2.9
Вычислить интеграл
Решение.
Т.к. (
,
то
Приводя к общему знаменателю и приравнивая соответствующие числители, получаем:
Итого:
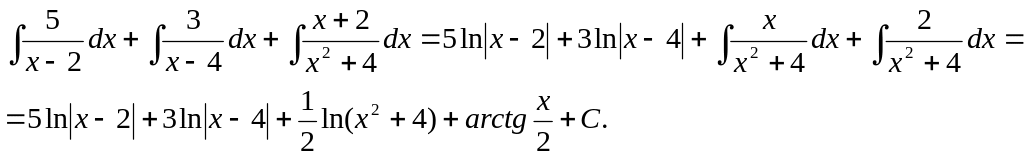
2.10
Вычислить интеграл
Решение. Т.к. дробь неправильная, то предварительно следует выделить у нее целую часть:
6
x5
– 8x4 – 25x3
+ 20x2 – 76x
– 7 3x3 – 4x2
– 17x + 6
6x5 – 8x4 – 34x3 + 12x2 2x2 + 3
9x3 + 8x2 – 76x - 7
9x3 – 12x2 – 51x +18
20x2 – 25x – 25
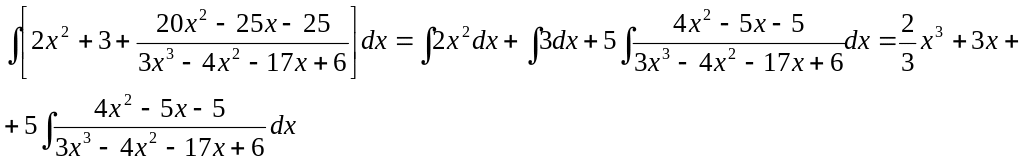
Разложим знаменатель полученной дроби на множители. Видно, что при х = 3 знаменатель дроби превращается в ноль. Тогда:
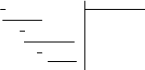3x3
– 4x2 – 17x
+ 6 x - 3
3x3 – 9x2 3x2 + 5x - 2
5x2 – 17x
5x2 – 15x
- 2x + 6
-2x + 6
0
Таким образом 3x3 – 4x2 – 17x + 6 = (x – 3)(3x2 + 5x – 2) = (x – 3)(x + 2 )(3x – 1). Тогда:
В полученное выше выражение подставим поочередно 3, -2, 1/3. Получаем:
Окончательно получаем:
=
2.11 Вычислить интеграл
2.12 Вычислить интеграл
2.13 Вычислить интеграл
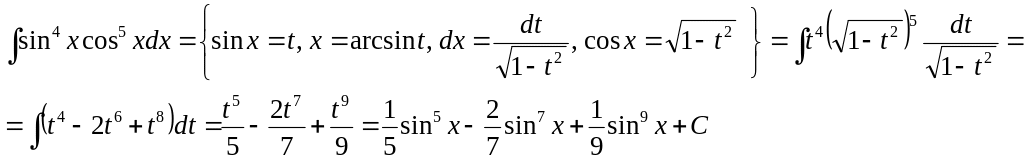
2.14 Вычислить интеграл
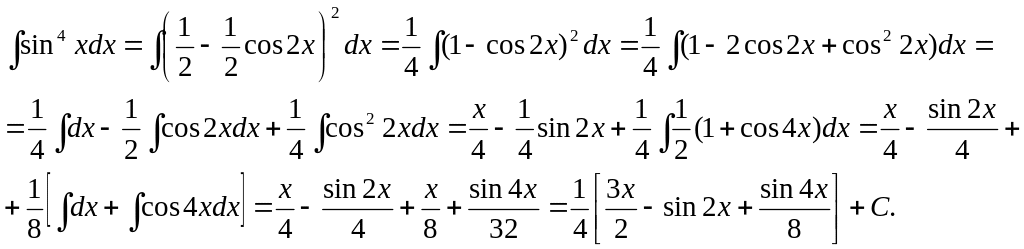
2.15 Вычислить интеграл
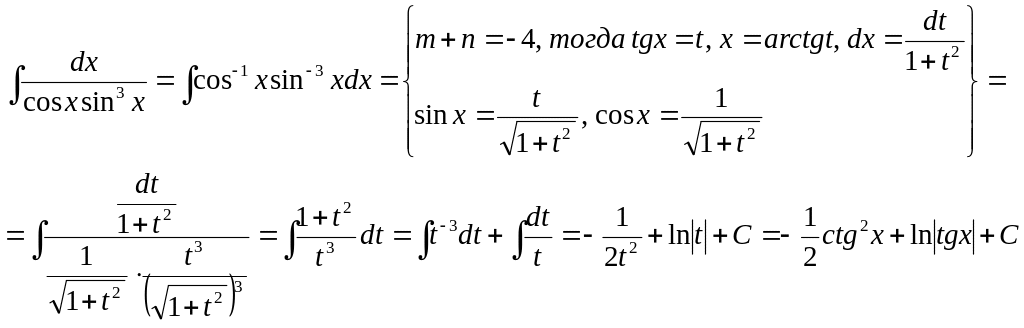
2.16 Вычислить интеграл
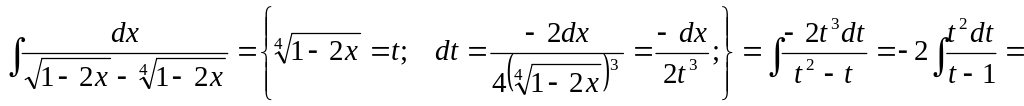
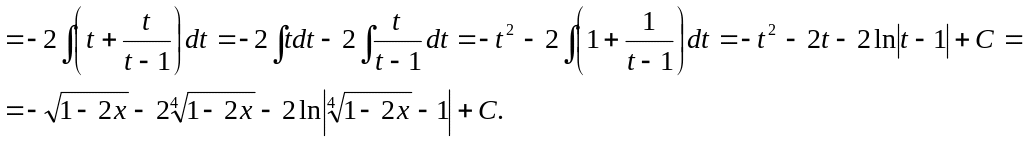
2.17 Вычислить интеграл
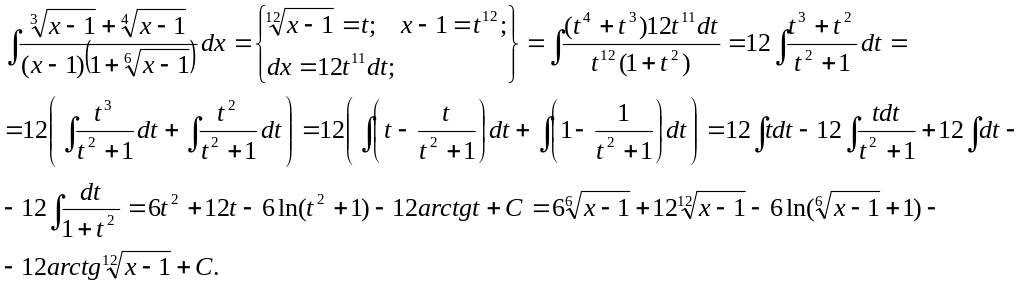
2.18 Вычислить интеграл
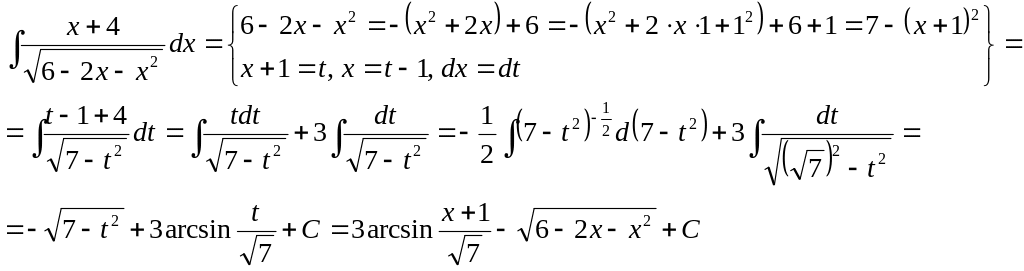
2.19 Вычислить интеграл
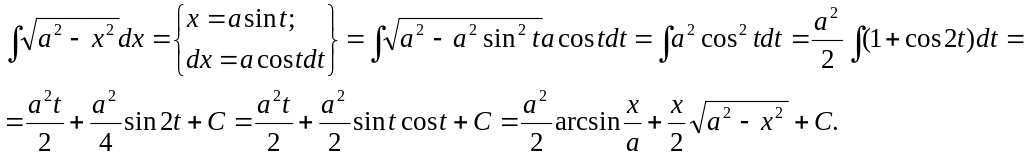
2.20 Вычислить интеграл
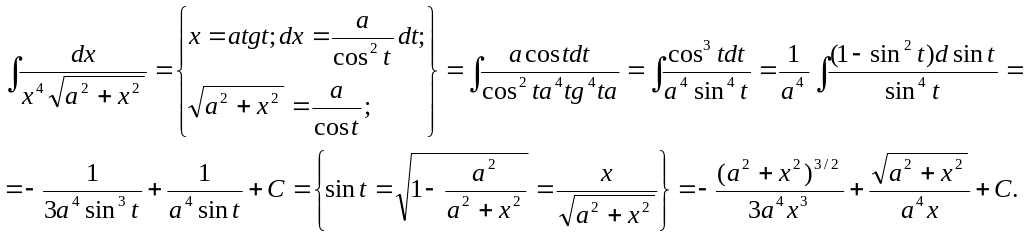
2.21 Вычислить интеграл
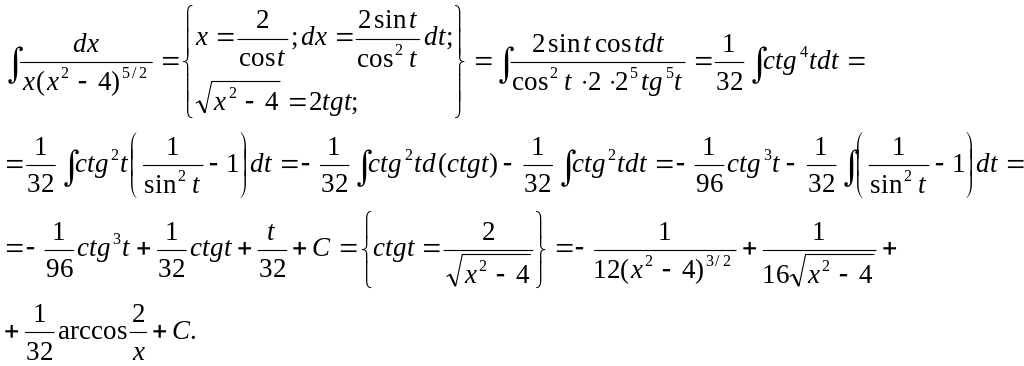
2.22 Вычислить определенный интеграл
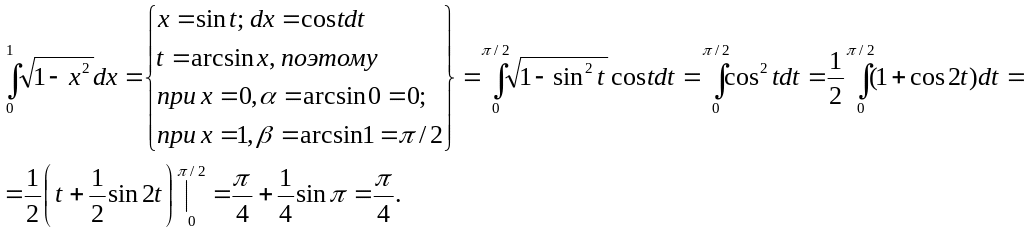
2.23 Вычислить определенный интеграл
2.24 Вычислить несобственный интеграл
-
не существует.
Несобственный интеграл расходится.
2.25 Вычислить несобственный интеграл
- интеграл сходится
2.26 Вычислить несобственный интеграл
2.27 Найти площадь фигуры, ограниченной линиями y = x, y = x2, x = 2.
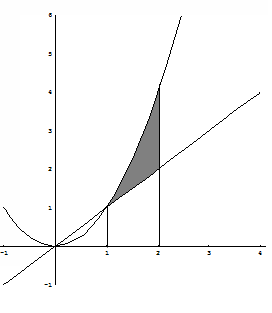
Решение. Искомая площадь (заштрихована на рисунке) может быть найдена по формуле:
(ед2)
Если криволинейная трапеция ограничена кривой, заданной параметрически
,
прямыми x=a,
x=b
и осью Ох, то площадь ее находится по
формуле
,
где α и β определяются из равенств х(α)=а и х(β)=b.
2.28 Вычислить площадь фигуры, ограниченной эллипсом x=cost, y=2sint.
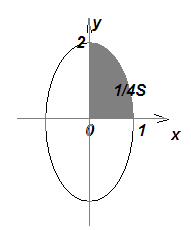
Решение. Площадь будем находить по формуле ,
Найдем сначала ¼ площади S. Здесь х изменяется от 0 до 1, следовательно t изменяется от π/2 до 0. Находим:
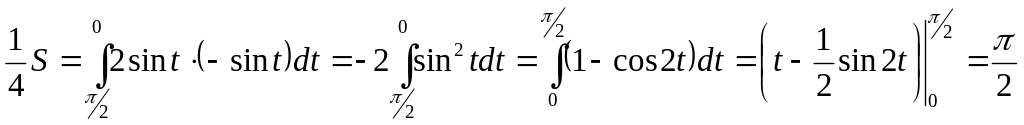(кв.ед.)
(кв.ед.)
2.29 Найти площадь фигуры, ограниченной линией r=cos3φ.
Решение. Площадь будем находить
по формуле
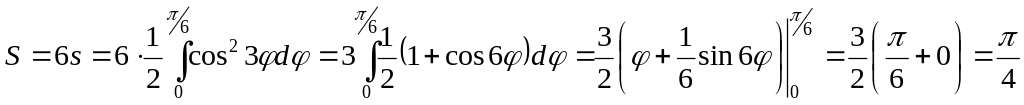
2.30 Найти длину окружности, заданной уравнением x2 + y2 = r2.
Решение.
1 способ. Выразим из уравнения
переменную у.
Найдем производную
Тогда из формулы
следует
Тогда S = 2r. Получили общеизвестную формулу длины окружности.
2 способ. Если представить заданное
уравнение в полярной системе координат,
то получим: r2cos2
+ r2sin2
= r2, т.е. функция
= f()
= r,
тогда из формулы
следует
способ. Если задать окружность параметрически
,
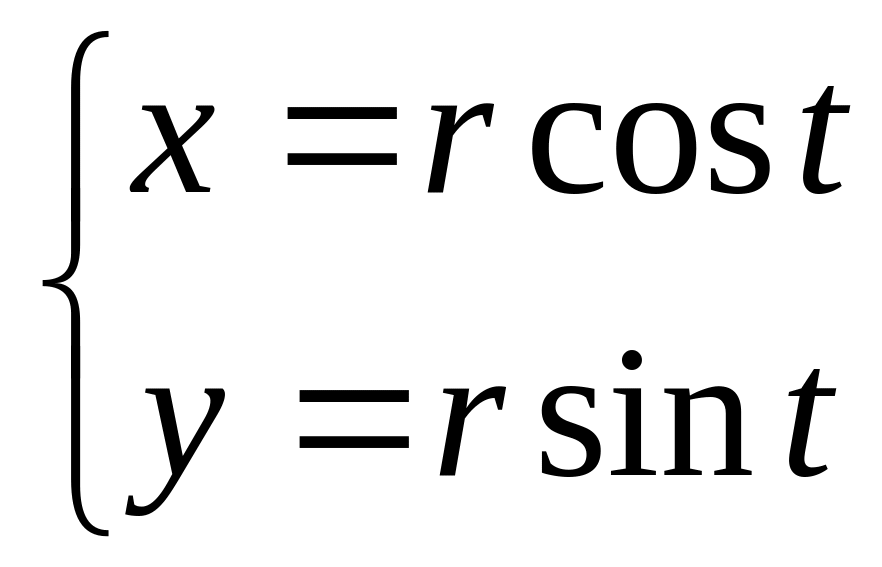тогда
и
,
следовательно
2.31 Найти объем тела, образованного
вращением фигуры, ограниченной линиями
вокруг
оси Оу.
Решение.
Находим:
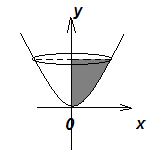
2.32 Вычислить приближенное значение определенного интеграла
с помощью формулы Симпсона, разбив
отрезок интегрирования на 10 частей.
Решение. По формуле Симпсона получим:
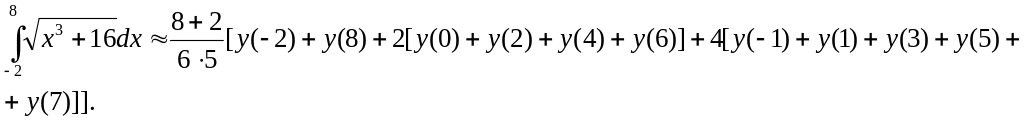
m |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
x |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
f(x) |
2.828 |
3.873 |
4 |
4.123 |
4.899 |
6.557 |
8.944 |
11.874 |
15.232 |
18.947 |
22.978 |
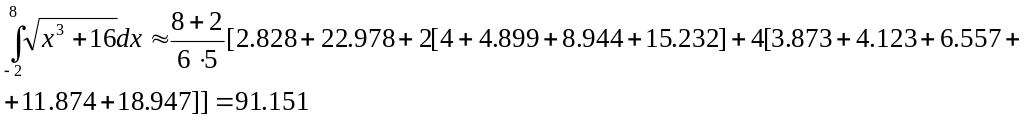
Точное значение этого интеграла – 91.173.