3.4. Критерий Стьюдента (t-критерий)

Для оценки значимости коэффициента корреляции генеральной совокупности делается предположение, что связь между случайными величинами x и y отсутствует и коэффициент корреляции r_xy = 0. Затем выбирают вероятность правдоподобия гипотезы (обычно Р = 0,95; 0,99), при этом можно говорить об уровне значимости  = 1 – Р. После этого вычисляется значение t-статистики:

,

где r_xy – коэффициент корреляции, рассчитанный по выборке, объёмом n (число пар наблюдений x и y). В соответствии с гипотезой Н₀ эта величина подчиняется распределению Стьюдента с (n-2)-мя степенями свободы. Обращаемся к таблице по t-статистике и ищем по ней вероятность (уровень значимости), соответствующую величине t для строки с (n-2)-мя степенями свободы. Если эта вероятность больше требуемой доверительной вероятности, то корреляция существует (r_xy  0) и гипотеза Н₀ о некоррелированности выборок отвергается с заданной вероятностью в пользу альтернативы Н₁.

Критерий Стьюдента используется также для проверки гипотезы о статистической значимости коэффициентов уравнения регрессии. В этом случае расчётное значение t-критерия записывается в виде:

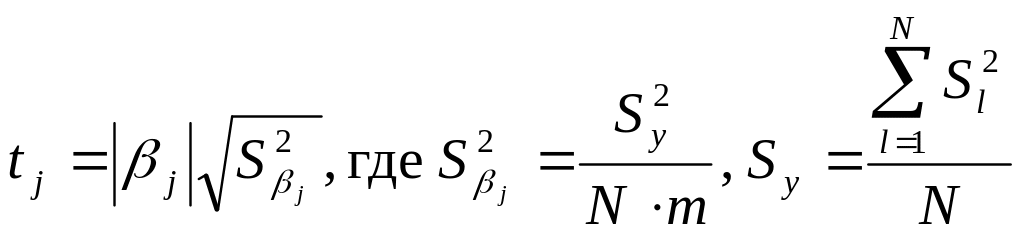
_j – коэффициент уравнения регрессии; S_j² – оценка дисперсии ошибки коэффициента регрессии по статистическим данным; S_y – дисперсия воспроизводимости; N – число опытов; S_l² – выборочное значение выходной величины y по l -той строке матрицы планирования, полученное из m параллельных опытов:

Табличное значение t-критерия находится при числе степеней свободы f = N(m-1) и уровне значимости q,%. Если t_j > t_крит, коэффициент уровня регрессии считается значимым.

3.5. Визуальный критерий проверки согласованности теоретических и статистических распределений (вариационная вероятностная сетка Турбина)

Проверку нормальности закона р аспределения можно выполнить, определённым образом преобразовав масштаб оси ординат (оси вероятностей). Для этого задаём верхним и нижним значениям вероятности более мелкий масштаб. В результате получаем вероятностную сетку, в которой куммулята нормального закона распределения превращается в прямую. Чем ближе точки значений лежат к прямой, тем с большей вероятностью можно утверждать о нормальности статистического закона распределения.

 Смотри раздел математической статистики