11 Оценка качества переходных процессов

По результатам интегрирования системы дифференциальных уравнений (43) осуществляется оценка качества переходных процессов в трансмиссии автомобиля, обусловленных включением сцепления.

Для оценка качества переходных процессов при включении сцепления используются следующие показатели:

1) коэффициент динамичности ;

2) максимальная мощность буксования , Вт;

3) суммарная работа буксования , Дж;

4) максимальное ускорение автомобиля , м/с².

Коэффициент динамичности переходного процесса характеризует нагруженность механизмов трансмиссии. Значения коэффициентов динамичности определяются для всех упругих элементов по формуле

; (48)

где – максимальное значение момента j-го упругого элемента в переходном процессе, Н·м;

– максимальный момент двигателя, Н·м;

– передаточное число трансмиссии от двигателя до j-го упругого элемента.

Для рассматриваемой динамической модели ; , где – передаточное число коробки передач; – передаточное число главной передачи.

Максимальная мощность буксования и суммарная работа буксования сцепления вычисляются в процессе моделирования по формулам (38) и (39). Одновременно вычисляются эти же показатели и для сцепления колес с дорогой.

От величины показателя зависит максимальная температура нагрева поверхностей трения сцепления, определяющая выгорание фрикционной накладки и ее разрушение. Показатель определяет объемную температуру нагрева фрикционных элементов и их износ.

Максимальное ускорение в переходном процессе при включении сцеплений характеризует комфортабельность автомобиля, так как создает неприятные ощущения для человека, обусловленные силами инерции, вызывающими продольный толчок автомобиля. Значение вычисляется по формуле

, (49)

где – максимальное угловое ускорение ведущих колес автомобиля, рад/с².

12 Определение максимальной скорости автомобиля

Одним из показателей тягово-скоростных свойств автомобиля является максимальная скорость , достигаемая в процессе разгона в заданных дорожных условиях. Согласно ГОСТ 22576–90 испытания по определению проводят на горизонтальном участке дороги с твердым покрытием. Поэтому можно принять следующие значения параметров характеристик дорожных условий: ; .

После достижения автомобиль продолжает двигаться с постоянной скоростью, поэтому значения угловых скоростей , а также моментов в упругих элементах постоянны, а производные их по времени равны нулю. Так как при этом деформация упругих элементов не изменяется, то относительные скорости вращения масс динамической модели трансмиссии равны нулю. Следовательно, равны нулю и потенциалы диссипативных элементов: . Движение автомобиля осуществляется на высшей передаче, что учитывается при выборе значений и . Сцепление автомобиля замкнуто, а колеса не проскальзывают, поэтому принимают , .

Используя исходную систему дифференциальных уравнений (16) и принимая во внимание отмеченные особенности, получаем следующую систему алгебраических уравнений:

(50)

Для вычисления вращающего момента двигателя используем исходное выражение (22), преобразуя его к виду:

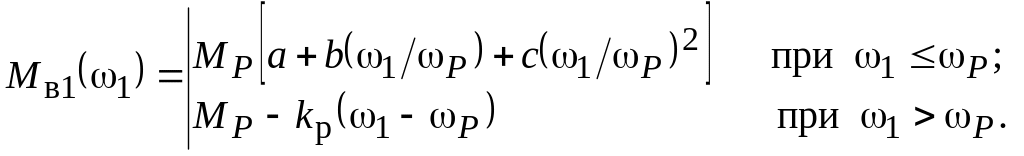(51)

При вычислении момента используются формулы (29)–(33).

Представим функцию внешнего воздействия в виде суммы двух составляющих – постоянной и переменной :

; (52)

, (53)

где . (54)

С учетом выражений (52) и (53) система уравнений (50) приводится к виду:

(55)

Решение системы алгебраических уравнений (55) позволяет определить значения фазовых координат , соответствующие скорости автомобиля в заданных дорожных условиях, характеризуемых параметрами и . В процессе решения уравнений (55) на каждом шаге итераций вычисляют вращающий момент двигателя , выполняя условия формулы (51). После решения системы уравнений (55) вычисляют значения вращающего момента двигателя и моментов сопротивления качению , сопротивления подъему и сопротивления воздуха . Вычислив затем отношения моментов , и к моменту , оценивают распределение затрат энергии двигателя на преодоление этих составляющих полного сопротивления.

Скорость автомобиля , км/ч, вычисляют по формуле

. (56)