8 Подготовка системы дифференциальных уравнений к выполнению

интегрирования

Для ввода информации о структуре и параметрах системы дифференциальных уравнений в ПЭВМ необходимо составить матрицу Якоби и вектор внешних воздействий. Примем во внимание, что искомыми фазовыми координатами системы являются . Следовательно, размерность матрицы Якоби 7×7, а вектора воздействий 7×1.

Выполним необходимые преобразования исходной системы уравнений (16). Для упрощения преобразований введем обозначение вектора внешних воздействий и составим выражения для вычисления его элементов:

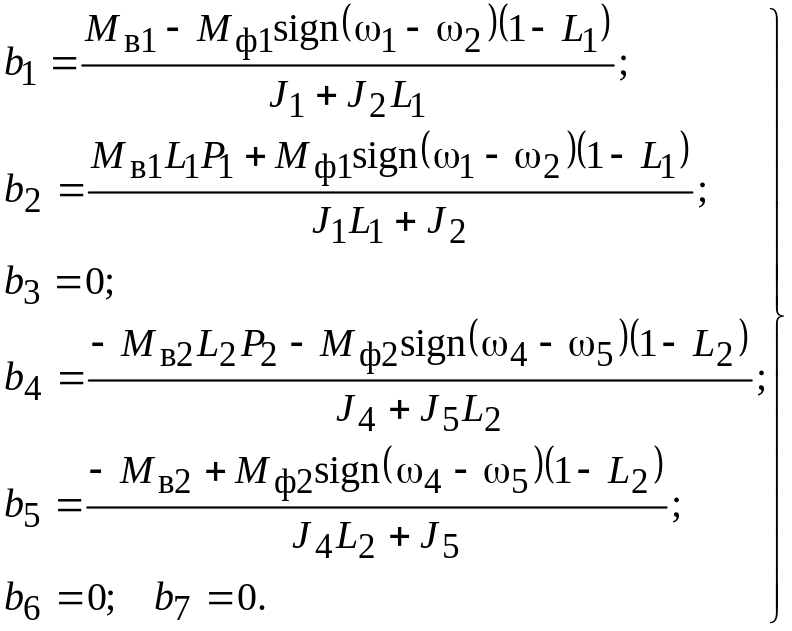(42)

Подставим в дифференциальные уравнения (16) значения потенциалов диссипативных элементов, используя компонентные уравнения (17), а также значения внешних воздействий, согласно выражениям (42):

(43)

На основе преобразованной системы дифференциальных уравнений (43) составляется матрица Якоби (таблица 3).

Так как элементы матрицы Якоби зависят от состояния фрикционных элементов, изменяющих структуру динамической модели, то их вычисление осуществляется на каждом шаге интегрирования. Кроме того, функции внешних воздействий также переменные. Необходимость пересчета элементов вектора внешних воздействий обусловлена зависимостью момента двигателя от угловой скорости коленчатого вала , определяемой выражением (22) (согласно динамической модели это зависимость от ), и зависимостью момента трения сцепления от времени (34).