20

Ф.Г. Будник, Е.С. Евтух

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА:

СТАТИКА, КИНЕМАТИКА

Утверждено редакционно-издательским советом университета

в качестве сборника заданий

Брянск

ИЗДАТЕЛЬСТВО БГТУ

2008

УДК 620.10 (07)

Будник, Ф.Г. Теоретическая механика:Статика, кинематика: сборник заданий /Ф.Г. Будник, Е.С. Евтух. – Брянск: БГТУ, 2008. – 112 с.

ISBN 5-89938-368-9

Включены задания для расчетно-графических работ по разделам теоретической механики «Статика», «Кинематика».

Сборник заданий предназначен для студентов всех форм обу­чения технических специальностей вузов, а также может быть полезен для инженеров и преподавателей.

Табл. 15. Ил. 65. Библиогр. – 3 назв.

Научный редактор Т.В. Селенская

Рецензенты: кафедра «Теоретическая и прикладная механика» Брянской государственной сельскохозяйственной академии;

доктор технических наук, профессор В.Т. Аксютенков

ISBN 5-89938-368-9  Брянский государственный

технический университет, 2008

Предисловие

В учебное пособие включены задания для расчетно-графических работ по разделам теоретической механики «Статика», «Кинематика» из учебного пособия «Сборник за­даний для курсовых работ по теоре­тической механике» под редак­цией А.А. Яблонского. Однако часть заданий (С1, С2, С3) подвергнуты существенной переработке.

Нумерация заданий выбрана так, чтобы они выполня­лись в той последовательности, в которой соответствующие задания выполня­ются на практических занятиях. Значительно переработана ме­тодика решения примеров заданий: изменилась последовательность решения задач, выбора объектов равновесия и составления уравнений равно­весия заданий, относящихся к разделу «Статика».

Обозначения параметров и единиц физических величин приве­дены в соответствие с последними рекомендациями учебной и науч­ной литературы по теоретической механике.

Раздел 1. Статика

I. Система сходящихся сил Задание с1. Определение реакций опор и усилий в стержнях

Плоской фермы

К одному из узлов плоской фермы приложена сила . Опреде­лить реакции опор фермы (с помощью теоремы о равновесии трех непараллельных сил), а также усилия во всех ее стержнях способом вырезания узлов. Вес стержней не учитывать. Основываясь на полу­ченных значениях усилий в стержнях, определить реакцию опоры А фермы вторым способом. Провести проверку определения усилий в стержнях, обозначенных номерами 4, 5, 6 на схемах ферм, методом Риттера.

Схемы ферм и необходимые для работы данные показаны на рис. 2,3,4.

Пример выполнения задания. Дано: схема фермы (рис. 1а), Р = 11 кН, α = 30°. Найти , и усилия в стержнях фермы.

а)

в)

б)

Рис. 1

Решение

Определение реакций опор

1. Объект равновесия – ферма.

2. Активная сила . Реакции связей (направлена по стержню), (согласно тео­реме о трех сила проходит через точку С).

3. На ферму действует плоская система сходящихся сил.

Записываем геометрическое условие равновесия

. (1)

Решаем векторное равенство (1) графически, т.е. строим си­ло­вой треугольник (рис. 1б). Из подобия силового треугольника и АВ₁С (рис. 1а), составляем пропорцию

.

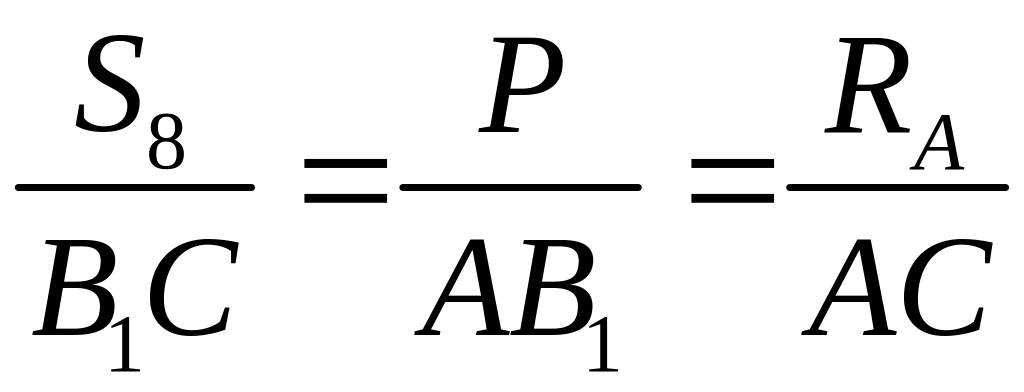Из рис. 1а получим В₁С = 3СЕ = 3а tgα = 3а = а .

.

Следовательно,

, откуда S₈ = P = 11 = 19,05 кН;

R_A = 2P = 2 11 = 22 кН.

Определение усилия в стержнях фермы методом вырезания уз­лов

Расчет начнем с выделения узла С.

1. Объект равновесия – узел С.

2. Силы

3. На узел С действует плоская система схо­дящихся сил.

Составим два уравнения равновесия сил

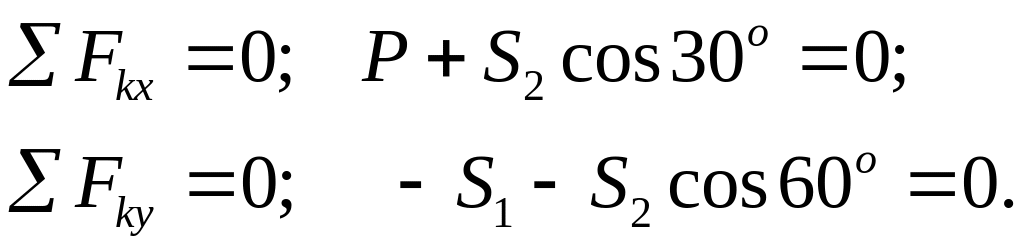
Откуда

кН;

кН.

Р

Р = 8 кН

Р = 7 кН

Р = 10 кН

Р = 8 кН

Р = 5 кН

Р = 5 кН

Р = 5 кН

Р = 12 кН

Р = 10 кН

Р = 10 кН

ис. 2

Р

Р = 5 кН

Р = 10 кН

Р = 10 кН

Р = 12 кН

Р = 5 кН

Р = 6 кН

Р = 5 кН

Р = 12 кН

Р = 12 кН

Р = 6 кН

ис. 3

Р

Р = 9 кН

Р = 10 кН

Р = 10 кН

Р = 12 кН

Р = 7 кН

Р = 8 кН

Р = 8 кН

Р = 5 кН

Р = 4 кН

Р = 8 кН

ис. 4

Далее вырезаем узел К.

1 .Объект равновесия узел К.

2. Силы .

3. На узел К действует плоская система сходя­щихся сил. Составим два уравнения равновесия для плоской системы сходящихся сил, действующих на вырезанный узел К.

; ;

; .

Подставляя в эти уравнения кН, получаем

кН;

кН.

Вырезаем узел Е.

1 . Объект равновесия узел Е.

2. Силы .

3. На узел Е действует плоская сис­тема сходящихся сил. Составим два урав­нения равновесия для плоской системы сходящихся сил, дейст­вующих на выре­занный узел Е.

; ;

; .

Откуда находим

кН;

кН.

Вырезаем узел L.

1. Объект равновесия узел L.

2. Силы .

3. На узел L действует плоская система сходящихся сил.

; ;

; .

Откуда находим

= 11 кН;

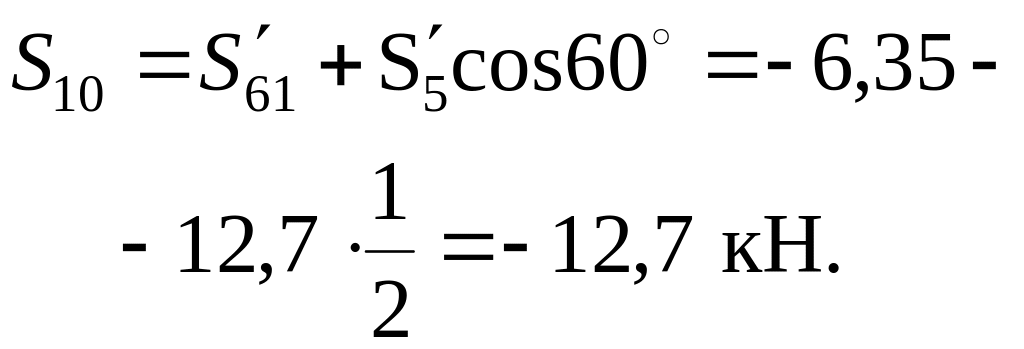Вырезаем узел В

1 . Объект равновесия узел В.

2. Силы .

3. На узел D дейст­вует пло­ская система сходя­щихся сил.

; .

Откуда находим

кН.

Для проверки вырезаем узел А.

1. Объект равновесия узел А.

2 . Силы .

3. На узел А действует плоская система сходящихся сил. Составим два уравнения рав­нове­сия для плоской сис­темы сходя­щихся сил.

; ;

;

.

Откуда находим

кН;

кН.

Возводя последние два уравнения в квадрат и складывая их, по­лучаем

.

Поскольку полученное значение реакции совпадает с ранее найденным её значением, то усилие в стержнях фермы определено верно.

Определяем усилия в стержнях фермы под номерами 4, 5, 6 ме­тодом Риттера. Для этого разрезаем ферму сечением b-b (рис. 1а) и рассмат­риваем равновесие сил, приложенных к одной, например, верхней части фермы.

1. Объект равновесия верхняя часть фермы (рис. 1в).

2. Активная сила . Усилия в стержнях .

3. На выделенную часть фермы действует плоская произвольная система сил. Составим три уравнения равновесия согласно ме­тоду Риттера.

Для определения составляем уравнение моментов относи­тельно точки Риттера Е, где пересекаются линии действия и :

.

Приняв , ,

получим

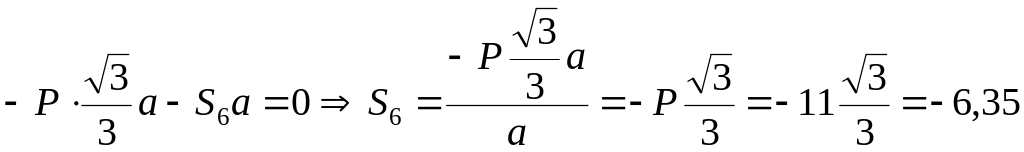кН.

Для определения проектируем силы на ось Ех:

; .

Откуда кН.

Для определения составляем уравнение моментов относи­тельно точки Риттера L, где пересекаются линии действия и :

; .

Так как ,

, то

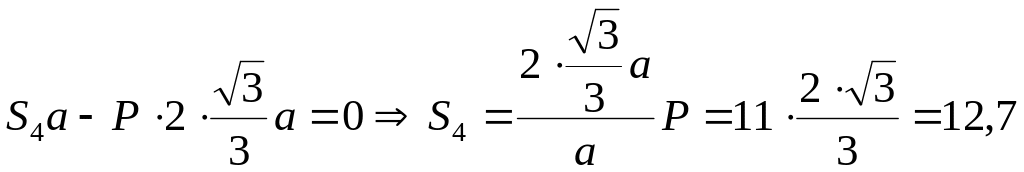кН.

Сравнивая результаты, полученные методом Риттера, с резуль­татами, полученными методом вырезания узлов, видно, что они сов­падают.

Задание С2. Определение усилий в стержнях

пространственной конструкции

Найти методом вырезания узлов усилия в шести стержнях шар­нирно-стержневой конструкции. Сила действует в направлении АВ, сила в вариантах 2,4 6,8,10 14,16 25,27,29,30 в направле­нии DE. Схемы конструкций показаны на рис. 6,7,8, а необходимые для расчетов данные приведены в табл. 1.

Таблица 1

Вариант (рис.6 8)	Нагрузка, кН		Размеры, м
	P	Q	прямоугольного параллелепипеда			d
			a	b	c
1	9		4,0	5,0	4,0	1
2	6	8	4,5	5,0	4,0
3	3	5	2,0	3,0	2,5
4	5	3	3,5	5,5	4,0
5	7	5	4,0	5,0	4,5
6	8	6	4,5	5,5	4,0
7	2		3,5	5,0	4,0
8	4	6	4,0	5,0	3,5
9	5	6	4,5	5,0	3,5
10	6	4	3,5	5,0	4,5
11	8	4	4,0	5,5	3,5
12	7	9	4,5	5,0	4,0
13	4	6	2,0	3,5	2,5
14	5	7	3,5	5,5	4,0	1,5
15	9		4,5	5,5	4,0
16	2	4	4,0	5,0	4,5
17	3	5	3,5	4,5	4,0
18	4	6	4,0	5,0	4,5
19	6	4	4,5	5,0	4,0

Продолжение табл. 1

Вариант (рис.6 8)	Нагрузка, кН		Размеры, м
	P	Q	прямоугольного параллелепипеда			d
			a	b	c
20	8	6	2,5	3,0	3,0
21	3	5	4,5	5,0	4,0
22	5	3	4,0	5,5	4,5
23	6	4	3,5	5,0	3,5	1,0
24	2	3	4,0	5,5	4,0
25	4	6	3,5	5,0	4,0
26	8		4,0	6,0	4,5
27	9	7	2,0	3,0	2,5
28	3		4,5	5,5	3,5	1,5
29	7	6	3,5	5,0	4,0	1,0
30	6	5	4,0	5,5	3,5