2.3. Применение теоремы Гаусса к расчету полей в вакууме

1. Поле равномерно заряженной бесконечной плоскости.

Бесконечная плоскость заряжена с поверхностной плотностью

,

где σ – заряд, приходящийся на единицу поверхности). Линии напряженности перпендикулярны плоскости и направлены в обе стороны от нее. В качестве замкнутой поверхности мысленно построим цилиндр, основания которого параллельны заряженной плоскости (рис. 2.7).

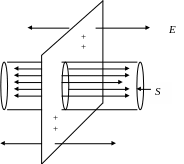
Рис. 2.7

Полный поток сквозь цилиндр равен сумме потоков через его основания, т.е. равен:

.

Согласно теореме Гаусса,

,

следовательно, напряженность поля равномерно заряженной бесконечной плоскости:

.

2. Поле двух бесконечных параллельных разноименно заряженных плоскостей.

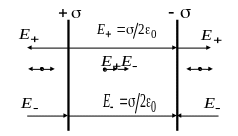
Плоскости заряжены с поверхностной плотностью и . Поле таких плоскостей найдем как суперпозицию полей, создаваемых каждой плоскостью. На рисунке верхние стрелки соответствуют полю от положительно заряженной плоскости, нижние – от отрицательной. Слева и справа от плоскостей Е = 0 (поля вычитаются, линии напряженности направлены навстречу друг другу). В области между плоскостями

,

т.е. – поле двух бесконечных параллельных разноименно заряженных плоскостей.

3. Поле равномерно заряженной сферической поверхности (рис. 2.8).

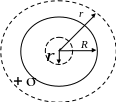
Рис. 2.8

Сферическая поверхность радиуса R общим зарядом Q заряжена равномерно с поверхностной плотностью + . Поле сферически симметричное, линии напряженности направлены радиально. Построим мысленно сферу радиуса r, имеющую общий центр с заряженной сферой. Если , то внутрь поверхности попадает весь заряд Q, создающий рассматриваемое поле, и, по теореме Гаусса

( ).

При поле убывает с расстоянием r по такому же закону, что и поле точечного заряда. Если , то замкнутая поверхность не содержит внутри зарядов, поэтому внутри равномерно заряженной сферической поверхности электростатическое поле отсутствует (Е = 0).

4. Поле объемнозаряженного шара. Шар радиуса R с общим зарядом Q заряжен равномерно с объемной плотностью

.

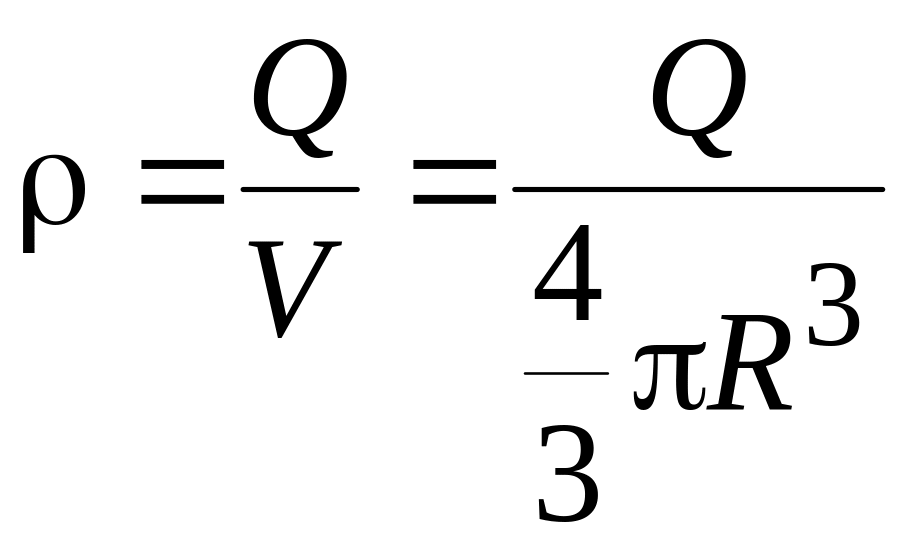Для напряженности поля вне шара, получится тот же результат, что и в предыдущем случае при r > R

.

Внутри шара напряженность поля другая. Сфера радиуса охватывает заряд

.

Согласно теореме Гаусса и учитывая, что

,

получаем

т.е. внутри равномерно заряженного шара напряженность растет линейно с расстоянием r от центра до значения

,

а затем убывает (рис. 2.9).

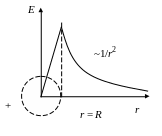
Рис. 2.9

5. Поле равномерно заряженного бесконечного цилиндра

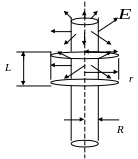
Рис. 2.10

Бесконечный цилиндр радиуса R заряжен равномерно с линейной плотностью τ (рис. 2.10).

.

Линии напряженности будут направлены по радиусам круговых сечений цилиндра с одинаковой густотой во все стороны относительно оси цилиндра. В качестве замкнутой поверхности мысленно построим цилиндр, коаксиальный с заряженным цилиндром радиуса r и высотой l. Поток вектора сквозь торцы цилиндра равен нулю (торцы параллельны линиям напряженности), а сквозь боковую поверхность .

По теореме Гаусса при r > R имеем:

,

следовательно, поле равномерно заряженного бесконечного цилиндра (нити):

,

при r > R.

Если r < R, то замкнутая поверхность зарядов внутри не содержит, поэтому в этой области Е = 0.