Лабораторная работа №4 изучить алгоритм прокладки маршрута и алгоритм полного обхода объекта.
Цель работы – выполнить обработку многоугольников (выпуклых, вогнутых), используя пошаговую функцию отслеживания контура для идентификации и классификации объектов. В конце изложить краткий вывод о результатах проделанной работы.
Алгоритмы и задачи выполнения лабораторной работы:
Выполнить идентификацию объекта – провести полный анализ характеристик заданного изображения, определить угловые и линейные характеристики, выполнить расчеты по определению площади фигуры внутри контура и найти центра масс.
Выполнить классификацию объекта – здесь необходимо определить количество сторон и углов заданного изображения, сделать вывод к какому классу оно относится (треугольник, окружность,…) либо указать на сходство с известными фигурами.
.
Пример выполнения лабораторной работы
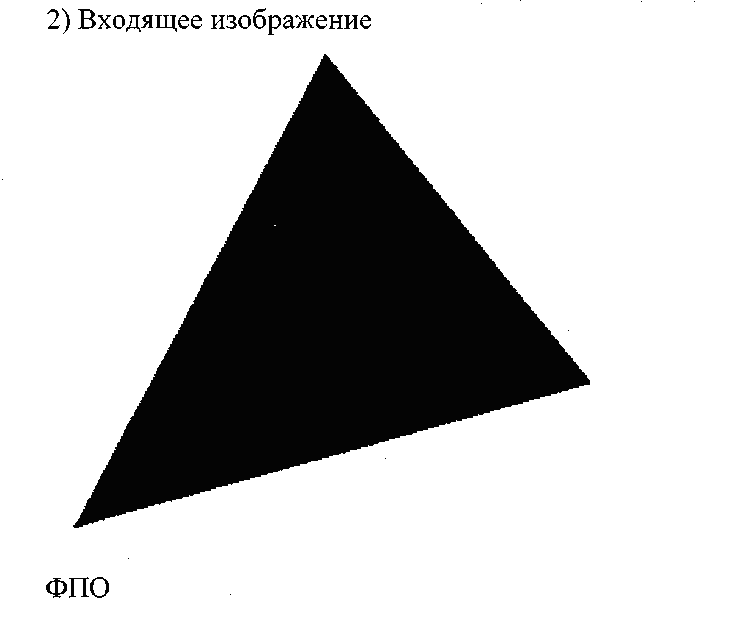
Последняя точка 415
Центр масс: 183, 224
Всего сторон после ФПО: 3
Сторона 1: длинна 104; угол наклона ФПО 0; вектор [О, 50] [104, 50]
Сторона 2: длинна 165; угол наклона ФПО 0; вектор [105, 163] [270, 163]
Сторона 3: длинна 151; угол наклона ФПО 0; вектор [271, 297] [422, 297]
=======================================================
Количество объединенных сторон: 3
Об. сторона 1: длинна 104; угол ФПО О
состоит из:
сторона: длинна 104; угол наклона ФПО 0; вектор [О, 50] [104, 50]
Об. сторона 2: длинна 165; угол ФПО О
состоит из:
сторона: длинна 165; угол наклона ФПО 0; вектор [105, 163] [270, 163]
Об. сторона 3: длинна 151; угол ФПО О
состоит из:
сторона: длинна 151; угол наклона ФПО 0; вектор [271, 297] [422, 297]
============ Описание объекта ============
Стороны: все грани плоские
Объект похож на треугольник
Описание треугольника: стороны 269, 343, 341; площадь 42489; углы 46, 67, 66 (град.)
- прямая длинной 267 пикселей и углом наклона-50 градусов
- прямая длинной 341 пикселей и углом наклона 15 градусов
- прямая длинной 340 пикселей и углом наклона 62 град
Вывод: в результате выполнения цикла работ были созданы программные модули, реализующие такие задачи:
построение функции пошагового обследования бинарного изображения
классификация и идентификация изображения
Лабораторная работа №5 обработка объектов с элементами постоянной кривизны.
Цель работы – выполнить обработку и анализ объектов с элементами постоянной кривизны, сделать вывод о результатах проделанной работы.
Алгоритмы и задачи выполнения лабораторной работы:
использовать алгоритм полного обхода объектов с последующим формированием функции отслеживания (т.к. задача определения кривизны сложна, то необходимо ввести ограничения на использование постоянной кривизны).
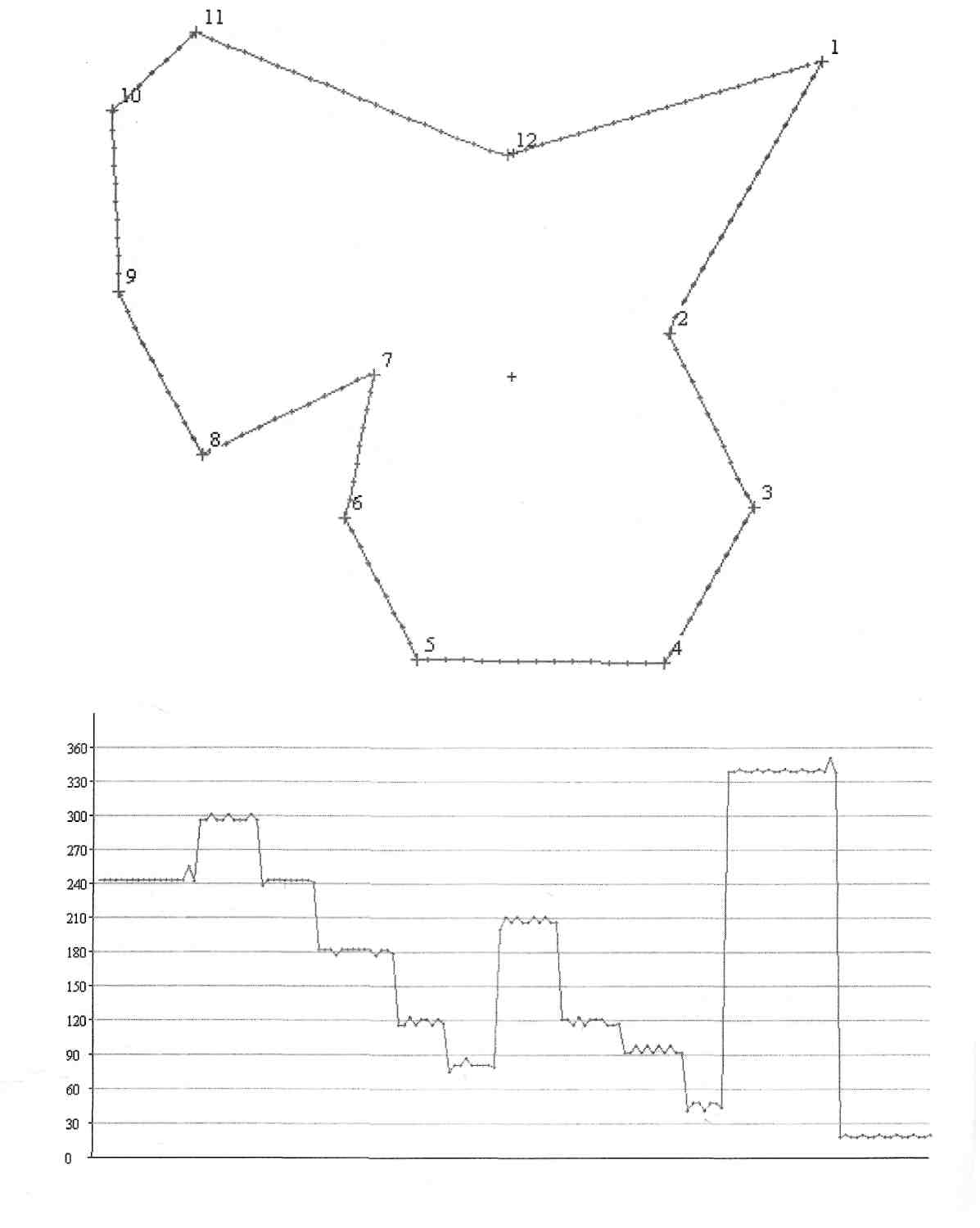
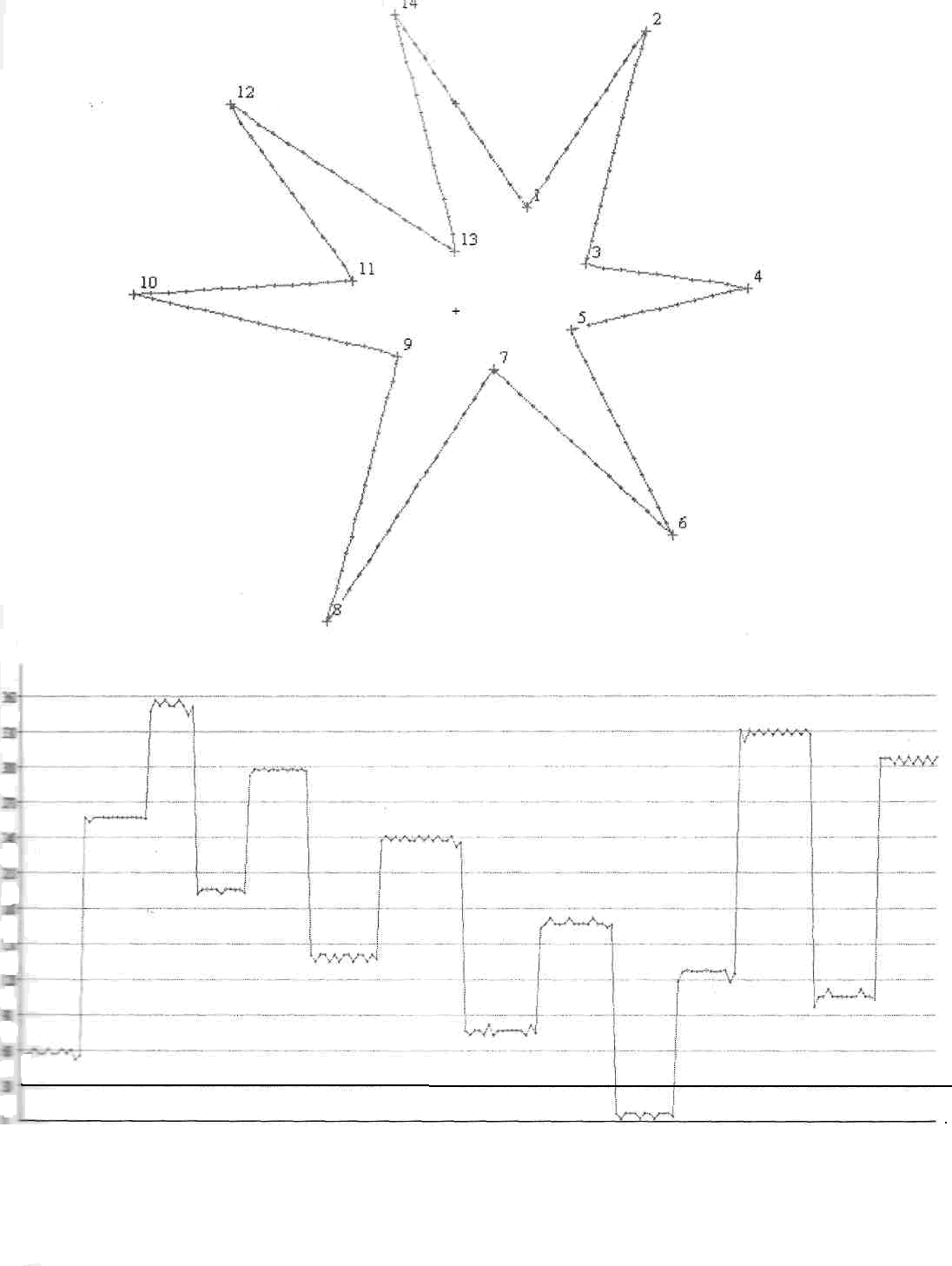
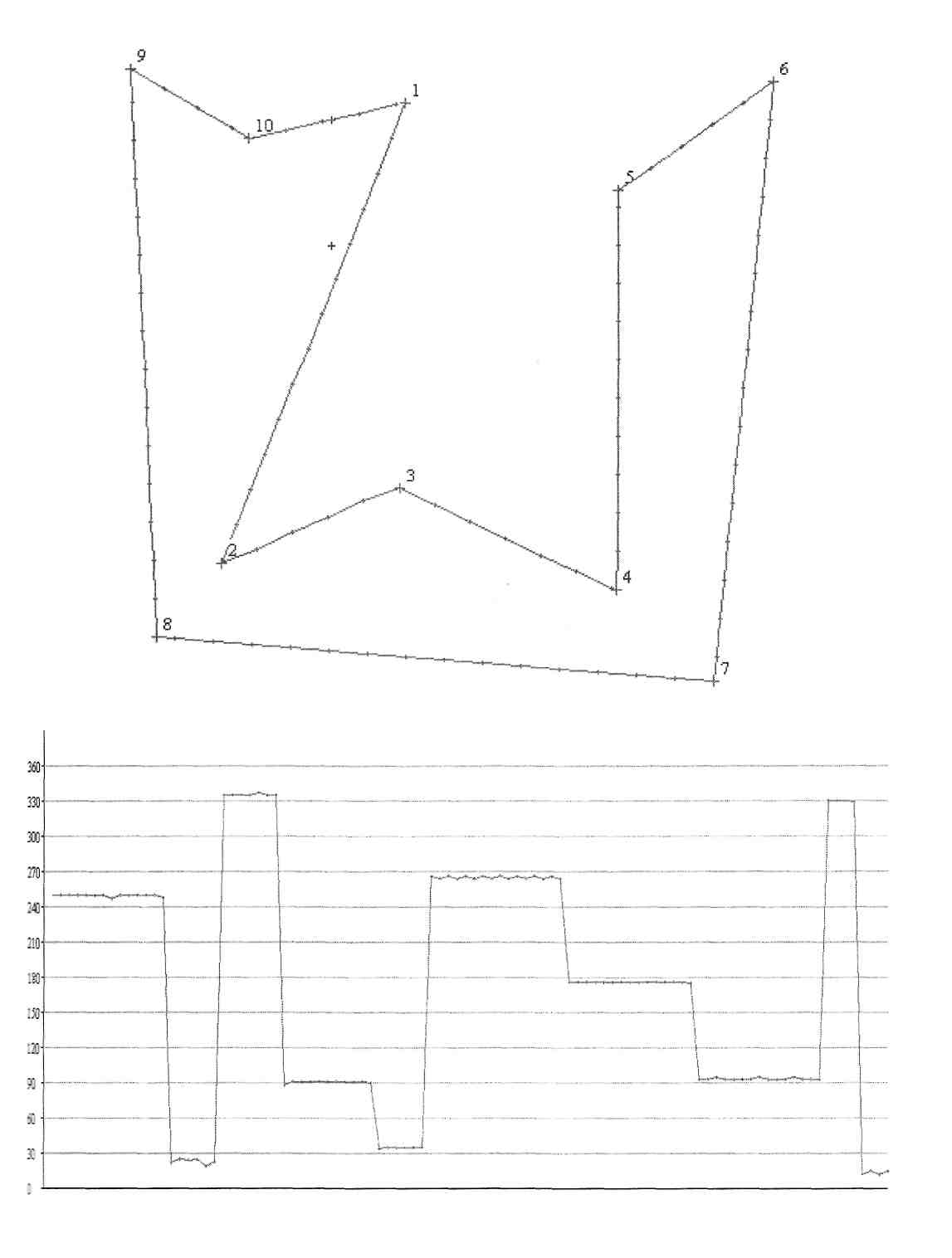
Наличие элементов кривизны определяется наклонными участками графика пошаговой функции отслеживания. В зависимости от положительной либо отрицательной кривизны на графике прослеживаются наклонные участки различного уклона.
идентифицировать объект с элементами кривизны
вычислить все линейные и угловые характеристики объекта (для криволинейного фрагмента контура определить радиус кривизны также определить длину криволинейного участка в количестве шагов, найти площадь и центр масс объекта)
выполнить классификацию объекта – из чего состоит контур, прямые и наклонные кривые.
Примеры объектов
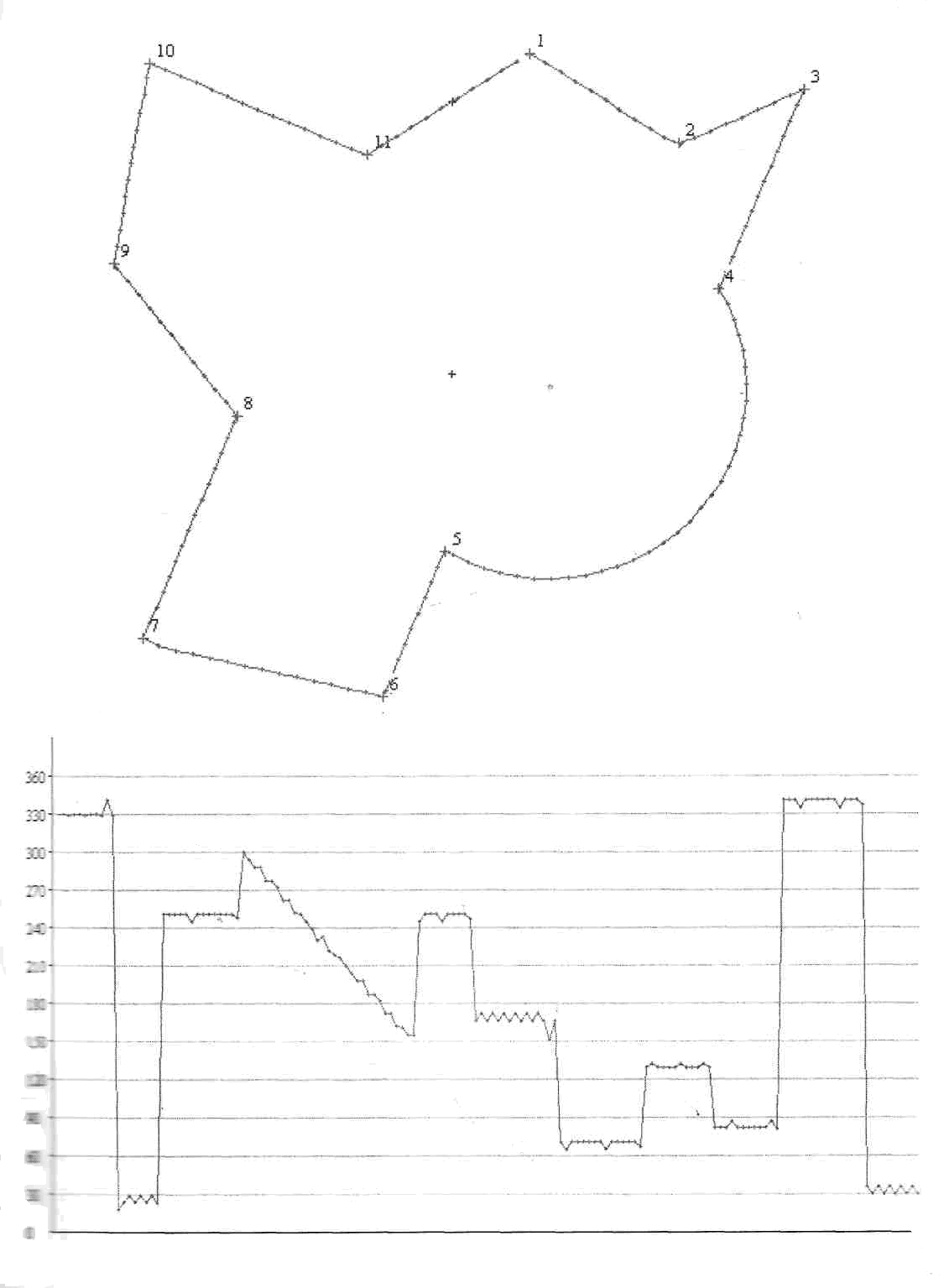
Пример выполнения лабораторной работы
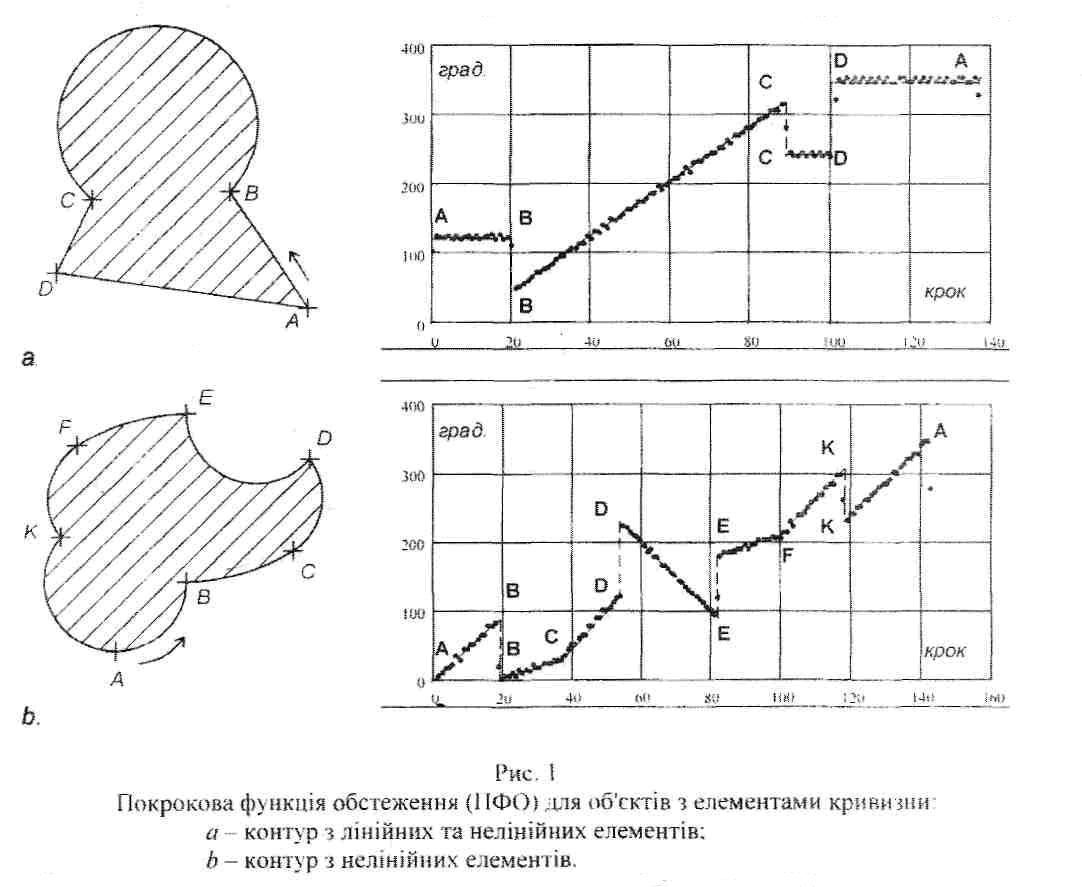
Процедуру распознавания объектов, контур которых включает определенные элементы кривизны, делиться на 2 этапа:
формирование ПФО
анализ ПФО
Условно будем считать, что исследование объекта начинается с точки А, хотя, в общем случае, формирование ПФО актуализуется любым образом. На рис 1 приведены ПФО для указанных двух объектов. Ось абсцисс при этом показывает последовательность шагов исследования; ось ординат определяет текущее значение направления исследования на каждом шаге и практически совпадает с направлением контура в заданной точке. ПФО адекватно отображает особенности контура исследуемого объекта. Линейным отрезкам контура отвечают фрагменты ПФО с постоянным направлением исследования; нелинейным фрагментам с постоянной кривизной отвечают линейные отрезки ПФО, наклон которых пропорциональный кривизне контура.