Государственный университет аэрокосмического приборостроения

АЛГОРИТМЫ РЕШЕНИЯ ЗАДАЧ НА ГРАФАХ И СЕТЯХ

Методические указания к выполнению

домашних заданий

Санкт-Петербург

2000

Составители: А.И. Бобков, В.Н. Макаренко

Рецензент: кандидат технических наук доцент Г.С. Евсеев

Даются методические указания к выполнению домашних заданий по основным разделам курса «Оптимизация технических решений». Указания содержат описание методов решения задач оптимизации на графах, которые используются для исследования структуры сложных программ, организации поиска информации и распределения памяти в информационных вычислительных системах. Предназначены для студентов специальности «Автоматизированные системы обработки информации и упрвления» целевой интенсивной и обычной подготовки.

Подготовлены к публикации кафедрой фвтоматизированных систем упраления по рекомендации методической комиссии факультета систем управления и электрооборудования летательных аппаратов Государственного университета аэрокосмического приборостроения.

I. Основные определения теории графов

Будем придерживаться терминологии из [1].

Ориентированным графом (орграфом) G=(Х, Г) называется пара (X, Г) , где X - множество элементов, называемых вершинами,

а Г -многозначное отображение Х =>Х . Многозначное отображение Х=>Х есть закон, по которому каждому элементу x принадлежащему Х ставится .в соот­ветствие некоторое подмножество Г_x множества Х . Дугами орграфа называется упорядоченные пары (x, y) принадлежащие Х*Х, y  Г_х. Если обо­значить через U множество всех дуг графа, то граф можно определить, как G= (X,U ) Вершина x называется началом дуги u = ( x , y ), а вершина y - ее концом. Дуга ( x , x ) , начало и конец которой совпадают, называется петлей. Две различные вершины x и y на­зываются смежными, если существует соединяющая их дуга.

Полустепенью захода вершины называется число дуг, заходящих я вершину, а полустепенью исхода - исходящих из вершины. Вершина S с нулевой полустепенью захода называется входом орграфа, а вершина t с нулевой полустепенью исхода - выходом орграфа.

Путем L (a, б) из вершины а, в вершину b называется после­довательность вершин и дуг a, (a, x₁), x₁, (x₁, x₂)…,(x_n-1, b),b. Заметим, что в орграфе путь однозначно определяется последователь­ностью вершин или дуг. Путь называется простым, если вершины не, повторяются. Если существует путь L(a, 6) , то говорят, что вер­шина b достижима из вершины a . Орграф называется связным, если для любой пары вершин одна достижима из другой.

Путь L (a, a), начала и конец которого совпадают, называет­ся контуром.

Пусть X₁, X₂ X, X₁ X₂=0, X₁ U X₂=X. Тогда множество <X₁, X₂> таких дуг, что для каждой дуги (х, у)  <X₁, X₂> выполня­ется условие, x X₂ , y X₂ буден называть разрезом графа G = (X, U) .

Неориентированным графом называется пара (X, U) , где X -множество вершин, а U - множество неупорядоченных пар элементов из X , называемых ребрами. Для неориентированного графа имеются почти все аналоги выше определенныx понятий.

Две вершины смежны, если они соединены; ребро инцидентно сво­им концевым вершинам; последовательность таких вершин x₁, x₂, … ,x_n, что (x_i-1, x_i) U образуют цепь; цепь, у которой совпадают концевые вершины, называется циклом; цепь и цикл являются простыми, если вершины не повторяются; две вершины х, y являются связанными, если существует путь L ( x, y ). Двудольным графом G= (R U S,U) называется граф для каждо­го ребра (x, y) U которого выполняется условие x R, y  S , т.е. инцидентные вершины всех ребер принадлежат двум разным под­множествам вершин.

Для описания графа будем использовать матрицу смежности или списки смежности. Матрицей смежности называется квадратная матрица Р , у которой p_ij=1, если (x_i,x_j)U (в случае взвешенного графа элемент p_ij равен весу дуги (ребра)), в противном слу­чав p_ij=0. Списки смежности перечисляют для каждой вершины x X множества Г_х , т.е. концов всех дуг, исходящих из вершины x.

2. Кратчайшие пути

Пусть G = (X, Г) - ориентированный граф, каждой дуге (x, y) которого приписано положительное число w (x, y) , называемое дли­ной дуги. Длиной пути называют сумму длин входящих в него дуг. Путь, имеющий наименьшую длину среди всех путей из s в t называют кратчайшим путем из s в t , а его длину - расстоянием между s и t .

Задача I. Необходимо найти кратчайшие пути и расстояния между данной вершиной s и всеми другими вершинами графа.

Рассмотрим алгоритм Дейкстры [2, 7]. Входными данными является орграф G=(X, Г) , матрица весов W={w(x, y)}; x, y X (все веса неотрицательные).

Опишем алгоритм Дейкстры, используя алголоподобный язык.

алгоритм I.

1) начало ;

2) для v X выполнить D(x):=w(i, v); D(s):=0;

3) T:=X\{s};

4) пока T <> 0 выполнить ;

5) начало ;

6) u:= произвольная вершина r T : D(r) = min {D(p) : p T /постоянная метка./; и для всех y T (r) w(y, r)=M

7) T:=T\{u} ;

8) для v  T выполнить D(v):=min(D(v), D(u) + w(u, v)); /временные метки/;

9) конец ;

10) конец.

В итоге работы алгоритма получим расстояния от вершины s до всех вершин графа (массив D(v) ).

Очевидно, что при входе в цикл 4 выполняются следующие усло­вия:

1) для каждой v  X\T D(v) = d(s, v) , где d(s, v) - кратчайшее расстояние от вершины s до вершины v ;

2) для каждой v T D(v) есть длина кратчайшего из тех путей из s , для которых предпоследняя вершина V\T.(1)

В строке 6 алгоритма находим u  Т , такую, что D(u) есть минимальное значение для всех u Т. В этом случае D(u) = d(s, u), так как если кратчайшее расстояние из s в u меньше D(u), то в силу второй части условия (I) предпоследняя вершина этого пути принадлежит Т . Пусть t - первая вершина пути, принадлежащая множеству Т .

Начальный отрезок пути из S в U (путь s-t. ) со­ставляет кратчайший путь из s в t , причем его предпоследняя вершина не принадлежит Т. Тогда, учитывая (I), имеем D(t) = d(s, t) . Так как все веса неотрицательные, получим: D(t)  d(s, u) < D(u) ,что противоречит принципу, по которому была выбрана вершина u. Т.о. D(u) = d(s, u) и в строке 7 мы уделяем вершину u из Т .

В цикле 8 проверяются пути из s в v  Т , предпоследняя вершина в которых есть U.

Оценим сложность алгоритма Дейкстры. Цикл 4 выполняется (n-1) раз, и каждое его выполнение требует o(n) шагов, (за •(n)) шагов находится вершина U в строке 6 и за o(n) шагов выполняется цикл 8). Таким образом, сложность алгоритма есть о(n²).

Пример I. Пусть в графе на рис.1 требуется найти кратчайшие пути из вершины s во все другие вершины графа. Длины дуг обозначены числами возле соответствующей дуги. Последовательное измене­ние меток вершин показано в табл.1. Окончательное распределение меток и кратчайшие пути показаны на рис.2.

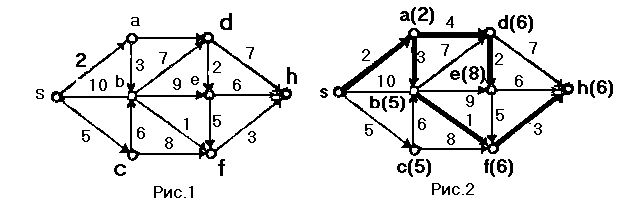
Таблица 1.

Вершина	Метки
s(x1)	0
a(x2)		2
b(x3)		10	5
c(x4)		5	5	5
d(x5)			6	6	6
e(x6)				14	14	8	8
f(x7)				6	6	6
h(x8)						13	9	9

Контрольные вопросы и задания

1. Докажите корректность алгоритма Дейкстры.

2. Приведите пример некорректности алгоритма в случае нару­шения условия w (i , j) > 0 для всех (i, j) U.

3. Предложите модификацию алгоритма, допускающую отрицатель­ные значения весов дуг.

4. Укажите последовательное изменение меток для длин дуг, при­веденных в табл.2, для графа, изображенного на рис.1.

5. Предложите модификацию алгоритма, если требуется найти кратчайший путь и его длину между двумя вершинами графа.

Таблица 2.

Дуги	Длины дуг
(s, a)	1	10	8	2	11	5	7	12	4	9
(s, b)	10	7	11	6	3	2	10	5	7	1
(s, c)	7	3	7	10	5	11	1	2	6	12
(a, b)	8	11	8	4	9	7	3	1	10	5
(a, d)	3	5	1	7	2	10	6	9	8	4
(b, d)	2	1	8	6	10	3	5	11	1	9
(b, e)	11	8	3	1	5	2	7	4	6	10
(b, f)	12	2	12	11	1	8	9	5	4	3
(c, b)	5	1	1	3	4	6	11	7	12	2
(c, f)	7	8	9	3	7	2	5	1	7	4
(d, e)	1	2	10	4	10	3	1	10	2	11
(d, h)	3	12	3	5	1	7	2	8	6	4
(e, h)	8	7	12	1	5	4	10	2	9	3
(e, f)	9	3	1	10	2	11	8	5	7	6
(f, h)	2	9	9	8	4	1	5	6	10	1

Задача 2. Необходимо найти кратчайшие пути между всеми пара­ми вершин графа G.

Рассмотрим алгоритм Флойда [1,2]. Пусть вершины графа G обозначены числами 1,2,..., n. Алгоритм строит последовательность матриц W⁽⁰⁾, W⁽¹⁾, W⁽²⁾,..., W⁽ⁿ⁾ следующим образом:

W^(k) : w_ij^(k) =min{w_ij^{(k - 1)},w_ik^{(k - 1)}+w_kj^{(k - 1)}},1 kn, (2)

w( i , j ), если ( i , j ) U,

W⁽⁰⁾ : w_ij⁽⁰⁾ = , если ( i , j ) U,

если i = j.

Элемент w_ij⁽ⁿ⁾ матрицы W⁽ⁿ⁾ равен расстоянию между вершинами i и j.

Обоснуем уравнение (2). Рассмотрим кратчайший путь из x_i в x_j с промежуточными вершинами из множества {x₁, …, x _k-1, x_k}.Если этот путь не содержит x_k, то,w_ij^(k) = w_ij^(k-1) деля путь на отрезки от x_i до x_k и от x_k до x_j, получаем равенство w_ij^(k) = w_ik^{(k -1)} + w_kj^{(k -1)} . Минимум

в (2) ищется по той причине, что необходимо определить кратчайшие расстояния между вер-шинами. Для определения кратчайших путей одновременно с последова­тельностью матриц { w^(k) } строится последовательность матриц Z⁽⁰⁾ , Z⁽¹⁾ , … , Z⁽ⁿ⁾ , где

Z^(k) : z_ij^(k) = z_ij^{(k -1)}, если w_ij^{(k –1)}  w_ik^(k-1) + w_kj^{(k -1)} . (4)

z_ik^{(k –1)} в противном случае.

Z⁽⁰⁾ : z_ij⁽⁰⁾ = j, если (i, j) U

0 в противном случае. (5)

Элемент z_ij⁽ⁿ⁾ матрицы Z⁽ⁿ⁾ указывает на первую вершину пос­ле i в кратчайшем пути из i в j . Кратчайший путь (i, i₁, i₂, …, ip, j) из вершины i в вершину j определяется по матрице Z⁽ⁿ⁾ следующим образом :

i₁ = Z_ij⁽ⁿ⁾ , i₂ = Z_{i1 j}⁽ⁿ⁾ , i₃ = Z_i2j⁽ⁿ⁾ ,… ,j = z⁽ⁿ⁾_ipj.

Входом алгоритма являются матрицы W⁽⁰⁾ и Z⁽⁰⁾ , построенные в соответствие с (3) и (5) . Пусть W⁽⁰⁾ = {w_ij} , Z⁽⁰⁾ = {z_ij} ,  - достаточно большое число М.

Алгоритм 2.

начало

1) для k от 1 до n шаг 1 цикл ;

2) начало ;

3) для i от 1 до n шаг 1 цикл ;

4) начало ;

5) для j от 1 до n шаг 1 цикл ;

6) начало ;

7) если w_ik + w_kj < w_ij , то ;

8) w_ij := w_ik + w_kj ;

9) z_ij := z_ik ;

10) конец цикла;

11) конец цикла;

12) конец цикла;

конец

Сложность этого алгоритма есть o(n³), так как алгоритм состоит из трех вложенных циклов, каждый из которых выполняется n раз.

Пример 2.

Пусть в графе, матрица которого представлена в форме табл.3, требуется найти кратчайшие пути между всеми парами вершин. Промежуточные результаты работы алгоритма представлены в табл. 5-14. Окончательные результаты представлены в табл. 15 и 16

Таблица 3 W⁽⁰⁾

1 2 3 4 5 6

0	5	M	4	7	M	1
M	0	3	6	M	2	2
1	9	0	8	M	3	3
M	10	M	0	2	M	4
9	M	3	5	0	3	5
6	1	M	M	8	0	6

Таблица 4 Z⁽⁰⁾

1 2 3 4 5 6

0	2	0	4	5	0	1
0	0	3	4	0	6	2
1	2	0	4	0	6	3
0	2	0	0	5	0	4
1	0	3	4	0	6	5
1	2	0	0	5	0	6

Таблица 5 W⁽¹⁾

1 2 3 4 5 6

0	5	M	4	7	M	1
M	0	3	6	M	2	2
1	6	0	5	8	3	3
M	10	M	0	2	M	4
9	14	3	5	0	3	5
6	1	M	10	8	0	6

Таблица 6 Z⁽¹⁾

1 2 3 4 5 6

0	2	0	4	5	0	1
0	0	3	4	0	6	2
1	1	0	1	1	6	3
0	2	0	0	5	0	4
1	1	3	4	0	6	5
1	2	0	0	5	0	6

Таблица 7 W⁽²⁾

1 2 3 4 5 6

0	5	8	4	7	7	1
M	0	3	6	M	2	2
1	6	0	5	8	3	3
M	10	13	0	2	12	4
9	14	3	5	0	3	5
6	1	M	7	8	0	6

Таблица 8 Z⁽²⁾

1 2 3 4 5 6

0	2	2	4	5	2	1
0	0	3	4	0	6	2
1	1	0	1	1	6	3
0	2	2	0	5	2	4
1	1	3	4	0	6	5
1	2	2	2	5	0	6

Таблица 9 W⁽³⁾

1 2 3 4 5 6

0	5	8	4	7	7	1
4	0	3	6	11	2	2
1	6	0	5	8	3	3
14	10	13	0	2	12	4
4	9	3	5	0	3	5
5	1	4	7	8	0	6

Таблица 10 Z⁽³⁾

1 2 3 4 5 6

0	2	2	4	5	2	1
3	0	3	4	3	6	2
1	1	0	1	1	6	3
2	2	2	0	5	2	4
3	3	3	4	0	6	5
2	2	2	2	5	0	6

Таблица 11 W⁽⁴⁾

1 2 3 4 5 6

0	5	8	4	6	7	1
4	0	3	6	8	2	2
1	6	0	5	7	3	3
14	10	13	0	2	12	4
4	9	3	5	0	3	5
5	1	4	7	8	0	6

Таблица 12 Z⁽⁴⁾

1 2 3 4 5 6

0	2	2	4	4	2	1
3	0	3	4	4	6	2
1	1	0	1	1	6	3
2	2	2	0	5	2	4
3	3	3	4	0	6	5
2	2	2	2	5	0	6

Таблица 13 W⁽⁵⁾

1 2 3 4 5 6

0	5	8	4	6	7	1
4	0	3	6	8	2	2
1	6	0	5	7	3	3
6	10	5	0	2	5	4
4	9	3	5	0	3	5
5	1	4	7	8	0	6

Таблица 14 Z⁽⁵⁾

1 2 3 4 5 6

0	2	2	4	4	2	1
3	0	3	4	4	6	2
1	1	0	1	1	6	3
5	2	5	0	5	5	4
3	3	3	4	0	6	5
2	2	2	2	5	0	6

Таблица 15 W⁽⁶⁾

1 2 3 4 5 6

0	5	8	4	6	7	1
4	0	3	6	8	2	2
1	4	0	5	7	3	3
6	6	5	0	2	5	4
4	4	3	5	0	3	5
5	1	4	7	8	0	6

Таблица 16 Z⁽⁶⁾

1 2 3 4 5 6

0	2	2	4	4	2	1
3	0	3	4	4	6	2
1	6	0	1	1	6	3
5	5	5	0	5	5	4
3	6	3	4	0	6	5
2	2	2	2	5	0	6

Контрольные вопросы и задания

I. Докажите корректность алгоритма Флойда.

2. Покажите, что матрица Р. , полученная из матрицы W⁽ⁿ⁾ следующим образом

p_ij = 0 , если w_ij⁽ⁿ⁾ = 0 или M

1 в противном случае,

является матрицей достижимости графа G.

3. Покажите, что если w_ij < 0 , то вершина i принадлежит контуру с отрицательной длиной.

4. Предложите процедуру определения кратчайших путей по мат­рице W⁽⁰⁾ и W⁽ⁿ⁾

5. Покажите, что многократное использование алгоритма Дейкстры для нахождения кратчайших путей между всеми парами вершин и ал­горитм Флойда имеют одинаковую вычислительную сложность.

6. Предложите модификацию алгоритма Флойда для случая неориен­тированного графа G.

7. Предложите процедуру определения числа М.