III. Лабораторное задание

1. С помощью компьютера выполнить тестовый опрос. Директория MICRO\LABWORK2\var x.bat.

2. Используя данные полученного варианта, выполнить задание по следующему плану:

2.1. Определить тип функции.

2.2. Построить график функции.

2.3. Используя программу из директории MICRO\POTREB\program.exe, построить карту кривых безразличия (три линии).

3. Перечислить свойства кривых безразличия.

IV. Содержание отчета

Отчет по лабораторной работе составляется каждым студентом.

Отчет должен содержать следующие результаты и выводы:

1. Тему и вариант работы.

2. Цель работы.

3. Аналитическое и графическое решение задачи.

4. Количество баллов, набранных при тестовом опросе.

V. Варианты к лабораторной работе

1. U = 4 ^. Y1 + 2 ^. Y2.

2. U = min (Y1/5, Y2/3).

3. U = 3 ^. Y1 + 4 ^. Y2.

4. U = min (Y1/5, Y2/4).

5. U = 2 ^. Y1 + 2 ^. Y2.

6. U = min (Y1/5, Y2/2).

7. U = 4 ^. Y1 + 4 ^. Y2.

8. U = min (Y1/4, Y2/3).

9. U = 4 ^. Y1 + 3 ^. Y2.

10. U = min (Y1/4, Y2/2).

11. U = 4 ^. Y1 + 2 ^. Y2.

12. U = min (Y1/3, Y2/4).

13. U = 3 ^. Y1 + 2 ^. Y2.

14. U = min (Y1/4, Y2/5).

15. U = 3 ^. Y1 + 3 ^. Y2.

Лабораторная работа №3 Производство и издержки. Иллюстрация процесса производства с помощью функции Кобба– Дугласа

I. Цель работы

1. Исследование издержек производства.

2. Построение графиков изоквант и изокост.

II. Общие сведения

Производственная деятельность – это процесс получения единицы продукции при определенной комбинации ресурсов ( L, K) и данном уровне технологии .Это можно записать с помощью производственной функции

Y=F (x₁, x₂),

где x₁ ,x₂ – ресурсы. Размерность 2 выбрана для удобства построения графиков.

Производственная функция характеризует зависимость между максимально возможным объемом выпуска (Q) и количеством применяемых ресурсов, например труда (L) и капитала (K). Так же как и для функции полезности и кривых безразличия, можно выделить, по крайней мере, 4 типа производственных функций:

1. Функция с полным взаимозамещением ресурсов

_, a₁>0,a₂>0.

2. Неоклассическая функция: ,

где , >0, .

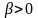3. Функция с полным взаимодополнением ресурсов:

.

4. Функция смешанного замещающе-дополняющего типа:

.

В теории производства традиционно используется двухфакторная производственная функция Кобба-Дугласа:

где П – объем продукции,

L – количество труда,

K – объем капитала,

A – коэффициент пропорциональности,

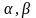- коэффициенты эластичности факторов производства.

Графически производственная функция - это линия равного выпуска-изокванта, подобная кривой безразличия. Если кривая безразличия характеризует один и тот же уровень полезности различных комбинаций потребительских благ, то изокванта – альтернативный вариант комбинаций факторов производства (например L и К) при определенном выпуске продукции. Таким образом, на карте выпуска каждая изокванта представляет множество комбинаций производственных ресурсов или технически эффективных способов производства определенного объема продукции. В отличие от кривых безразличия каждая изокванта характеризует определенный объем выпуска.

Функция издержек – изокоста – показывает те затраты на покупку факторов производства, которые может позволить себе фирма. Если цены факторов производства будут меняться, то изокоста меняет свой наклон.

Определение оптимального объема производства при минимальных издержках предполагает точку касания производственной функции и функции издержек. Используя краткосрочную производственную функцию неоклассического типа, можно изобразить изокванты и изокосты, а также графики средних и предельных затрат, проиллюстрировать таким образом основы теории производства.