
ФОРМУЛА ПЛОЩАДИ ЭЛЛИПСА:
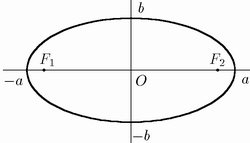
1) Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи (3.1415).
![]()
S - площадь эллипса
π - число пи (3.1415)
a - длина большой полуоси
b - длина малой полуоси
Формулы объема
Объём геометрической фигуры - количественная характеристика пространства, занимаемого телом или веществом. В простейших случаях объём измеряется числом умещающихся в теле единичных кубов, т. е. кубов с ребром, равным единице длины. Объём тела или вместимость сосуда определяется его формой и линейными размерами.
ФОРМУЛА ОБЪЕМА КУБА:
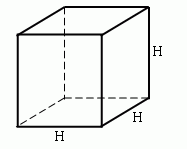
1) Объем куба равен кубу его ребра.
![]()
V - объем куба
H - высота ребра куба
ФОРМУЛА ОБЪЕМА ПИРАМИДЫ:
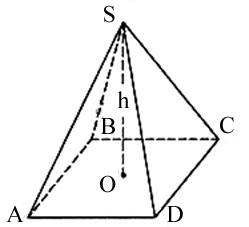
1) Объем пирамиды равен одной трети произведения площади основания S (ABCD) на высоту h (OS).
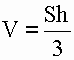
V - объем пирамиды
S - площадь основания пирамиды
h - высота пирамиды
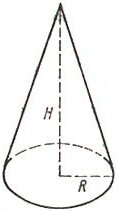
ФОРМУЛЫ ОБЪЕМА КОНУСА:
1) Объем конуса равен одной трети произведения площади основания на высоту.
2) Объем конуса равен одной трети произведения числа пи (3.1415) на квадрат радиуса основания на высоту.
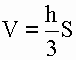 ,
,
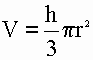
V - объем конуса
S - площадь основания конуса
h - высота конуса
π - число пи (3.1415)
r - радиус конуса
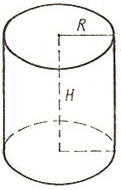
ФОРМУЛЫ ОБЪЕМА ЦИЛИНДРА:
1) Объем цилиндра равен произведению площади основания на высоту.
2) Объем цилиндра равен произведению числа пи (3.1415) на квадрат радиуса основания на высоту.
![]()
![]()
V - объем цилиндра
S - площадь основания цилиндра
h - высота цилиндра
π - число пи (3.1415)
r - радиус цилиндра
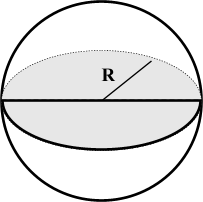

V - объем шара
π - число пи (3.1415)
R - радиус шара
ФОРМУЛА ОБЪЕМА ТЕТРАЭДРА:
1) Объем тетраэдра равен дроби в числителе которой корень квадратный из двух помноженный на куб длины ребра тетраэдра, а в знаменателе двенадцать.
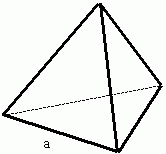
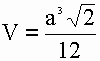
V - объем тетраэдра
a - длина ребра тетраэдра
Формулы треугольника
Треугольник - фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки - его сторонами.
ФОРМУЛЫ ПЛОЩАДИ ТРЕУГОЛЬНИКА
Площадь геометрической фигуры - часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади треугольника выражается числом заключающихся в него квадратных единиц.
1-АЯ ФОРМУЛА
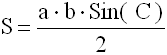
S - площадь треугольника
a, b - длины 2-х сторон треугольника
С - угол между сторонами a и b
2-АЯ ФОРМУЛА
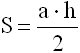
S - площадь треугольника
a - длина стороны треугольника
h - длина высоты, опущенной на сторону a
3-ЬЯ ФОРМУЛА
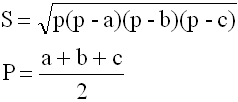
S - площадь треугольника
a, b, c - длины 3-х сторон треугольника
p - полупериметр треугольника
4-АЯ ФОРМУЛА
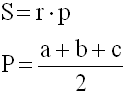
S - площадь треугольника
r - радиус вписанной окружности
p - полупериметр треугольника
5-АЯ ФОРМУЛА
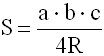
S - площадь треугольника
a, b, c - длины 3-х сторон треугольника
R - радиус описанной окружности
Формула периметра треугольника
Периметр геометрической фигуры - суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина.
1) Периметр треугольника равен сумме 3-ех его сторон (a, b, c).
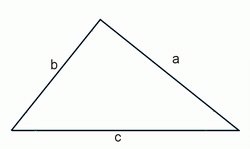
![]()
P - периметр треугольника
a, b, c - длины сторон треугольника
Формулы круга и окружности
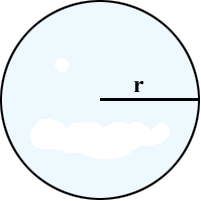
Круг - геометрическое место точек плоскости, расстояние от которых до данной точки не больше, чем заданное ненулевое.
Окружность - замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая. Также круг можно определить как часть плоскости, ограниченную окружностью.
Формула площади круга:
Площадь геометрической фигуры - часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади круга выражается числом заключающихся в него квадратных единиц.
1) Площадь круга равна произведению квадрата радиуса на число пи (3.1415).
2) Площадь круга равна половине произведения длины ограничивающей его окружности на радиус.
![]()
S - площадь круга
π - число пи (3.1415)
r - радиус круга
ФОРМУЛА ПЕРИМЕТРА КРУГА (ДЛИНЫ ОКРУЖНОСТИ):
Периметр геометрической фигуры - суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина.
1) Периметр круга равен произведению радиуса на два пи (3.1415).
![]()
P - Периметр круга (длина окружности)
π - число пи (3.1415)
r - радиус круга (окружности)
Формулы трапеции
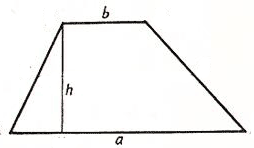
Трапеция - четырёхугольник, у которого две стороны параллельны (основания трапеции), а две другие - непараллельны (боковые стороны трапеции). Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
ФОРМУЛА ПЛОЩАДИ ТРАПЕЦИИ:
Площадь геометрической фигуры - часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади трапеции выражается числом заключающихся в него квадратных единиц.
1) Площадь трапеции равна произведению полусуммы ее оснований на высоту (a, b, h).
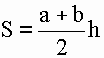
S - площадь трапеции
a - длина 1-ого основания
b - длина 2-ого основания
h - длина высоты трапеции
ФОРМУЛА ПЕРИМЕТРА ТРАПЕЦИИ:
Периметр геометрической фигуры - суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина.
1) Периметр трапеции равен сумме 4-х её сторон (a, b, c, d).
![]()
P - периметр трапеции
a, c - длины оснований трапеции
b, d - длины боковых сторон трапеции
Формулы квадрата
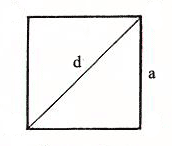
Квадрат — правильный четырёхугольник, у которого все стороны и углы равны между собой. Может быть определён как прямоугольник, у которого две смежные стороны равны между собой, или как ромб, у которого все углы прямые. У квадрата есть две диагонали, соединяющие несмежные вершины.
ФОРМУЛЫ ПЛОЩАДИ КВАДРАТА:
Площадь геометрической фигуры - часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади квадрата выражается числом заключающихся в него квадратных единиц.
1) Площадь квадрата равна квадрату длины его стороны (a).
2) Площадь квадрата равна половине квадрата длины его диагонали (d).
![]()

S - площадь квадрата
a - длина стороны квадрата
d - длина диагонали квадрата
ФОРМУЛЫ ПЕРИМЕТРА КВАДРАТА:
Периметр геометрической фигуры - суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина.
1) Периметр квадрата равен сумме 4-х длин его сторон или произведению длины любой его стороны на четыре (так как у квадрат длины всех сторон равны).
2) Периметр квадрата равен произведению длины его диагонали на два корня из двух.
![]()
![]()
P - периметр квадрата
a - длина стороны квадрата
d - длина диагонали квадрата
Формулы прямоугольника
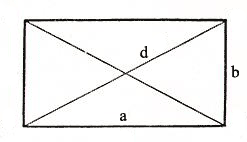
Прямоугольник - это четырёхугольник, у которого четыре прямых угла. Размеры прямоугольника задаются длинами его сторон, обозначаемых обычно a и b. Прямоугольник, все стороны которого равны (a = b) называется квадратом.
ФОРМУЛА ПЛОЩАДИ ПРЯМОУГОЛЬНИКА:
Площадь геометрической фигуры - часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади прямоугольника выражается числом заключающихся в него квадратных единиц.
1) Площадь прямоугольника равна произведению длин двух его смежных сторон (a, b).
![]()
S - площадь прямоугольника
a - длина 1-ой стороны прямоугольника
b - длина 2-ой стороны прямоугольника
ФОРМУЛА ПЕРИМЕТРА ПРЯМОУГОЛЬНИКА:
Периметр геометрической фигуры - суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина.
