Задача № 6

Исследовать функцию и построить схематично её график.

Решение.

1. Областью определения данной функции являются все действительные значения аргумента : .

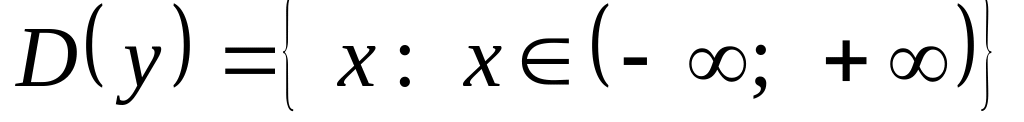2. Определим точки пересечения графика функции 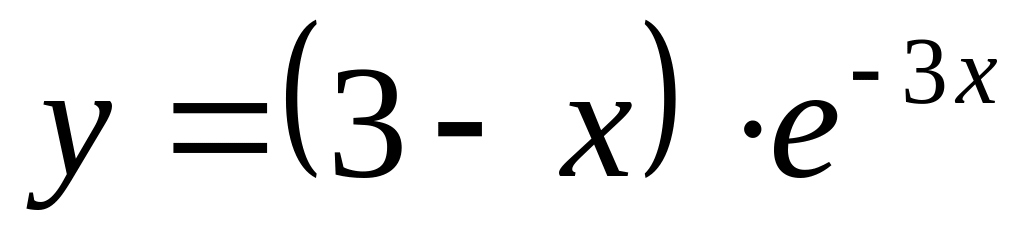с осями координат:

• с осью 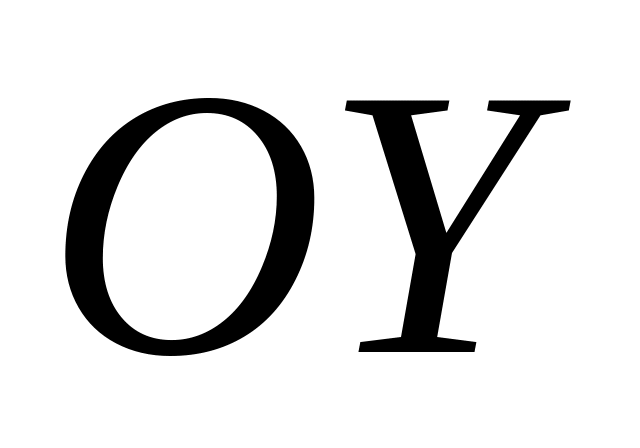при : ;

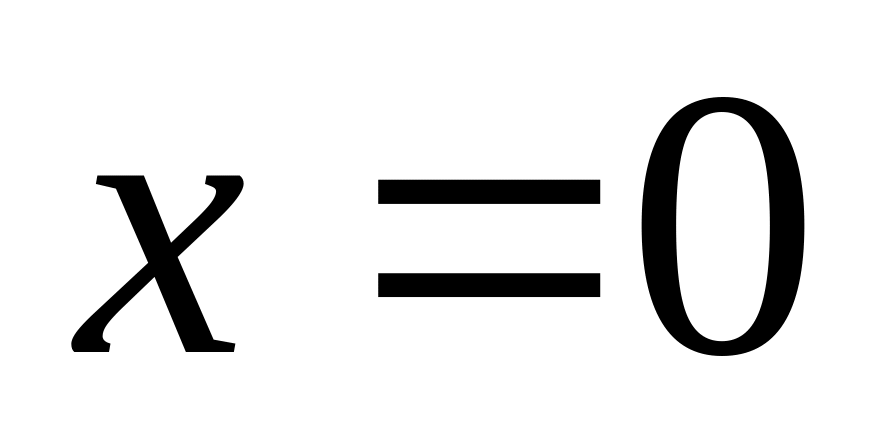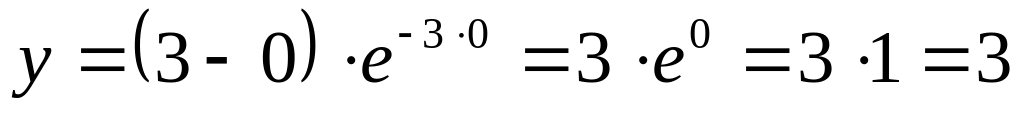Точка – точка пересечения графика функции с осью ;

• с осью 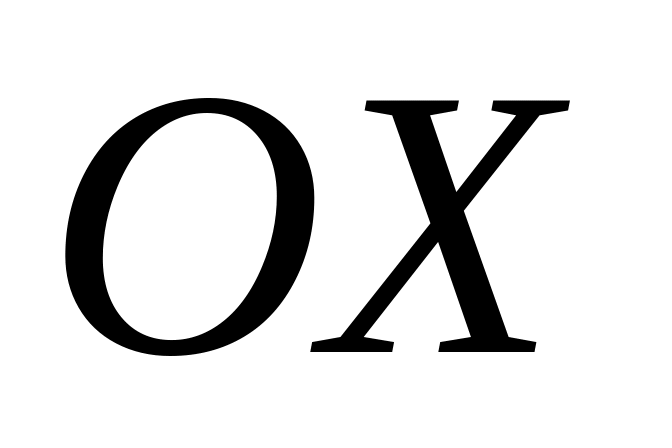при : ; ; .

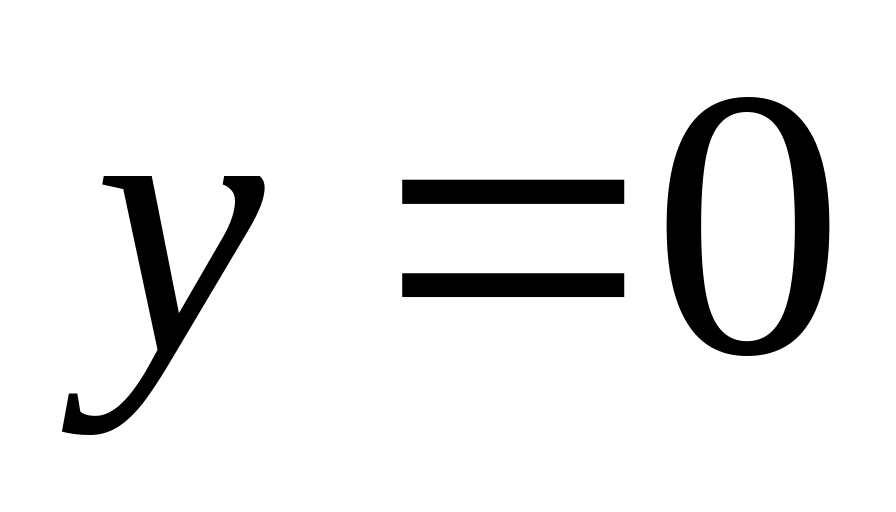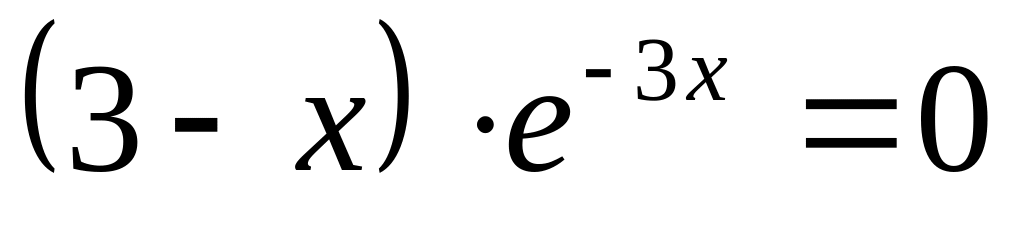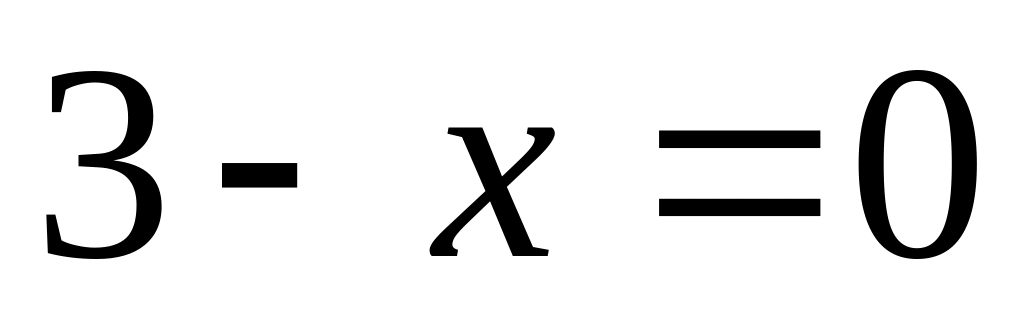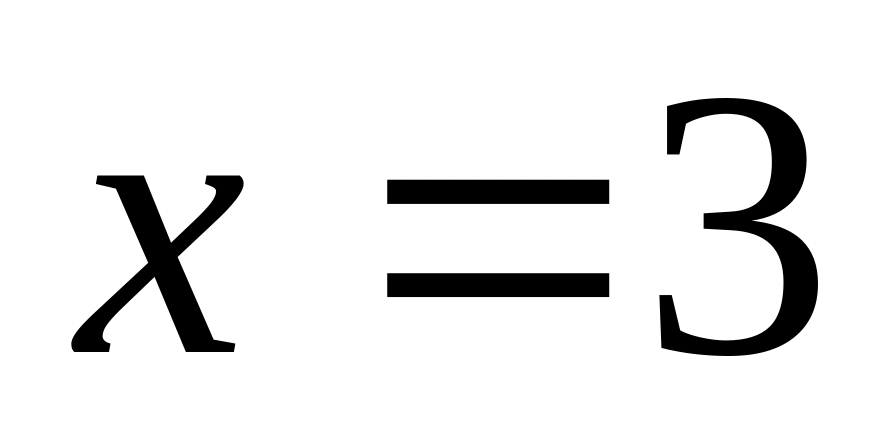Точка – точка пересечения графика функции с осью .

3. Функция не является ни чётной, ни нечётной так как

и , .

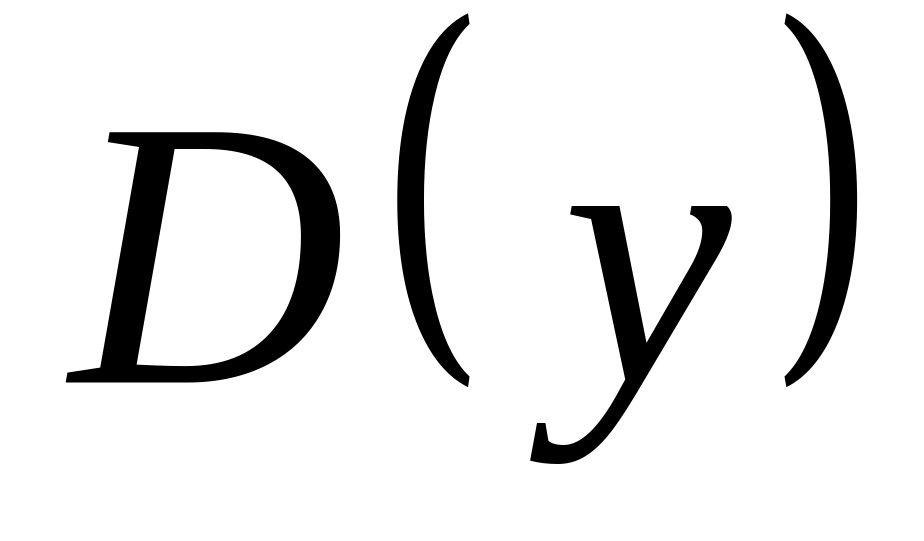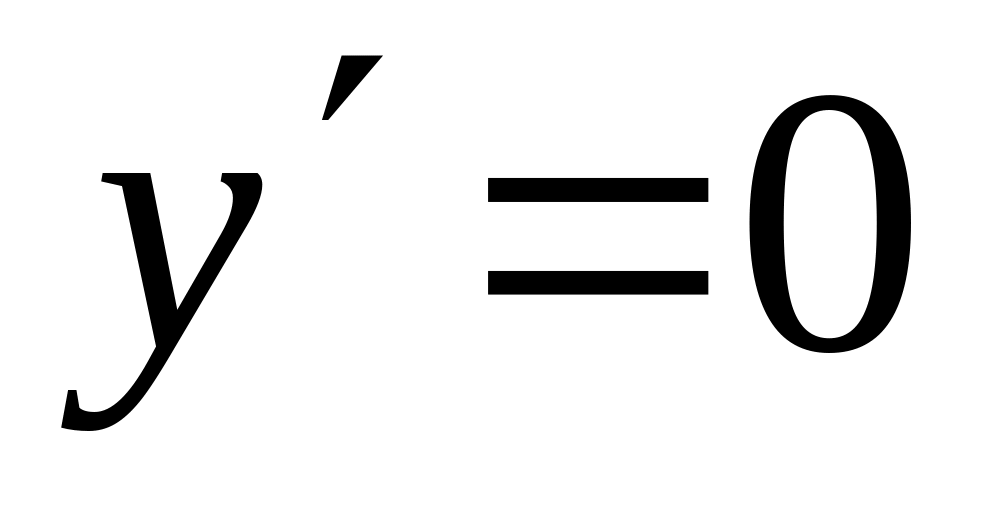4. Определим точки возможного экстремума, то есть точки из , в которых производная либо не существует.

.

существует при всех , то есть при .

при , то есть при ; .

Значит – единственная точка возможного экстремума, которая разбивает на два интервала: и .

Определим знак в каждом из этих интервалов по знаку для произвольной точки из соответствующего интервала:

х
	–	0	+
у

Функция убывает при и возрастает при .

При переходе через точку меняет знак, значит функция имеет экстремум в точке .

При переходе через точку меняет знак с «–» на «+», значит является точкой минимума функции.

, .

Точка – точка минимума функции .

5. Определим точки возможного перегиба, то есть точки из , в которых вторая производная либо не существует.

.

существует при всех , то есть при .

при , то есть при ; .

Значит – единственная точка возможного перегиба, которая разбивает на два интервала: и .

Определим знак в каждом из этих интервалов по знаку для произвольной точки из соответствующего интервала:

х
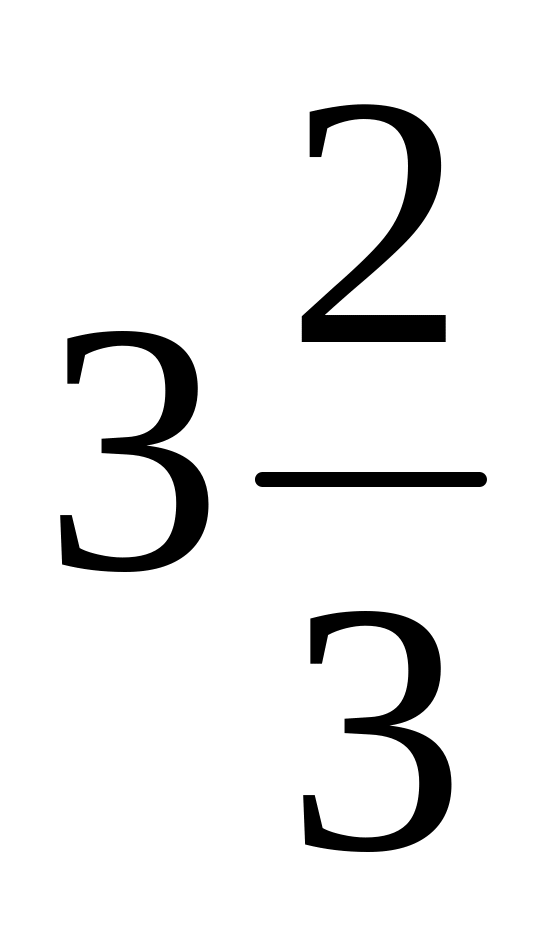
	+	0	–
у

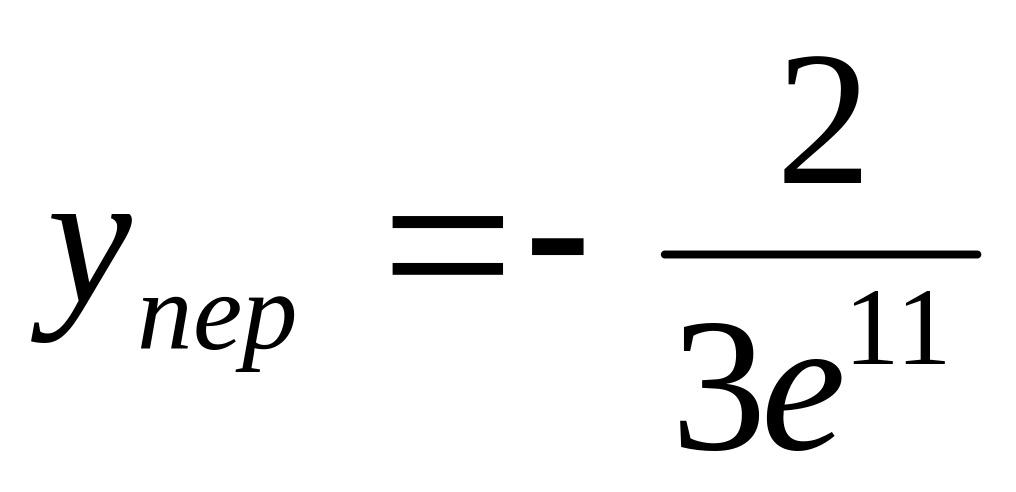
При график функции вогнутый, а при – выпуклый.

При переходе через точку меняет знак, значит график функции имеет перегиб в точке .

, .

Точка – точка перегиба графика функции .

6. Исследуем функцию на наличие у её графика асимптот.

Вертикальных асимптот график функции не имеет, так как функция непрерывна на всей числовой прямой.

Проверим наличие у графика функции невертикальных (наклонных, горизонтальных)

асимптот вида при , где , .

,

,

следовательно, прямая , то есть прямая , совпадающая с осью , является горизонтальной асимптотой графика функции на .

Проверим наличие у графика функции невертикальных (наклонных, горизонтальных)

асимптот вида при , где , .

,

следовательно, невертикальных (наклонных, горизонтальных) асимптот у графика функции на нет.