Кинематика колеса.

Движение колеса имеет сложную структуру. Колесо перекатывается по поверхности дороги теоретически без проскальзывания, в то время как в действительности проскальзывание существует, но составляет сравнительно небольшую величину.

Введём три системы координат: xy – неподвижную относительно поверхности дороги; x1y1 – подвижную относительно поверхности дороги; x1y1 – подвижную и связанную с рамой велосипеда или осью колеса, x2y2 – подвижную и связанную непосредственно с колесом, которая, таким образом, совершает сложное движение. Система координат x1y1 совершает переносное поступательное движение, в котором все точки имеют одинаковую скорость V. Система координат x2y2 совершает относительное вращательное движение, в котором каждая точка колеса движется с окружной скоростью Vp = wp, где w – угловая скорость относительного движения; p – расстояние от начала координат O1 до рассматриваемой точки. Векторная сумма переносной и относительной скоростей любой точки колеса равна абсолютной скорости Va=V+Vp

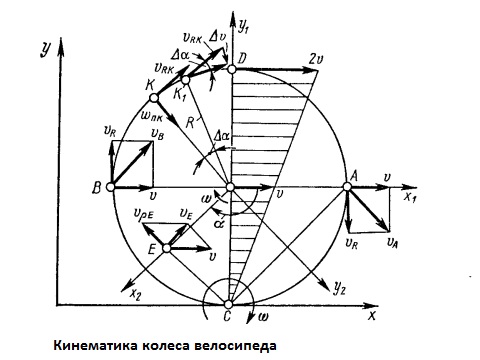
Точка C является точкой касания колеса с поверхностью дороги и является неподвижной при принятом выше условии – отсутствии проскальзывания колеса относительно дороги и деформации однотрубки. Скорость точки С, принадлежащей колесу (p=R), равна

Для произвольной точки E колеса, находящейся на расстоянии p=O1E от оси колеса, скорость определится как векторная сумма Ve=V+VpE. Численное значение скорости точки E может быть определено с помощью выражения

С другой стороны, плоскопараллельное движение колеса в каждый момент времени можно представить как вращение около мгновенного центра вращения. В данном случае мгновенным центром вращения является мгновенный центр скоростей в точке C, в котором скорость равна нулю. Положение мгновенного центра скоростей можно определить также как точку пересечения перпендикуляров к направлениям векторов абсолютных скоростей двух произвольных точек колеса, например А и Е.

Тогда скорость любой точки колеса определяется выражением V=wp, где W – угловая скорость вращения колеса вокруг мгновенного центра скоростей, равная угловой скорости вращения колеса вокруг своей оси O1; p – расстояние от рассматриваемой точки до мгновенного центра вращения. Так, для точки D это расстояние составляет Pd=2R, для точек A и B будет Pв=Pа=Rsqrt2; для произвольной точки Е

Направлен вектор абсолютной скорости в сторону вращения перпендикулярно к соответствующему отрезку P, соединяющему мгновенный центр скоростей с рассматриваемой точкой.

Окружная скорость любой i-й точки Vri направлена по касательной к траектории её движения относительно оси вращения колеса O1. По мере увеличения угла “a” точка A последовательно занимает положения C, B и D, а вектор Vri, оставаясь постоянным по величине, меняет своё направление. Это объясняется наличием нормального ускорения движения даже при равномерном вращении колеса, т.е. при тангенциальном ускорении, равном нулю. При бесконечно малом угле поворота delta(a), на который колесо поворачивается за бесконечно малый промежуток времени delta(t), скорости в точках K и K1 представляют собой равные по величине векторы Vrk и Vrk1, касательные к окружности в этих точках. Перенеся вектор скорости Vrk в точку K1 получим вектор delta(V), представляющий собой изменение скорости точки K при переходе в положение K1 за время delta(t). Из подобия треугольников и с учётом того, что delta(t)->0, можно записать

Отсюда следует, что нормальное ускорение точки K

Это ускорение направлено к центру колеса и называется центростремительным. В случае неравномерного движения полное ускорение складывается из нормального и тангенциального, которые взаимно перпендикулярны:

Кинетостатика системы

При движении велогонщик и велосипед образуют единую движущуюся систему, в которой силы взаимодействия являются внутренними и сами по себе не могут обеспечить движения общего центра масс системы. Для движения необходимы внешние силы, которые в данном случае сводятся к силам тяжести, силам трения колёс о дорожное покрытие и силам аэродинамического сопротивления.

Для начала рассмотрим отдельно взятые ведущее и ведомое колёса велосипеда, а затем систему гонщик-велосипед в целом.

Ведущее колесо.

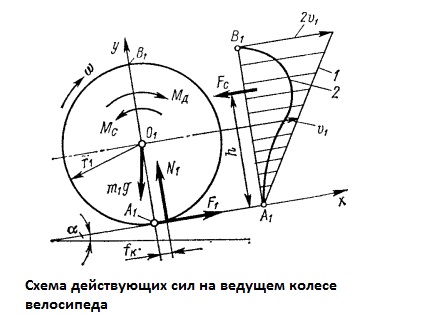
К ведущему колесу массой m1 с моментом инерции J1 приложен движущий момент Mд, под действием которого со стороны дороги возникает сила трения скольжения F1=fN1, где N1 – сила нормального давления; f – коэффициент трения скольжения. Точка A1 является мгновенным центром вращения и её скорость равна нулю. Поэтому f есть коэффициент трения покоя, величина которого неопределенна и может принимать значения от 0 до fmax. Эпюра скоростей 1 в диаметральном сечении колеса A1B1 является фактически эпюрой скоростей набегающего воздушного потока, сила сопротивления которого Fe, приложенная в центре масс эпюры 2 суммарного лобового и вихревого сопротивлений, создаёт момент полного аэродинамического сопротивления Мe.

Колесо, имеющее пневматическую шину в виде однотрубки, деформируется в зоне контакта с поверхностью дороги, что приводит к смещению реакции N1 на некоторую величину fк, называемую коэффициентом трения качения Mк1=fкN1. Учитывая малось величины fк, в дальнейшем будем считать реакцию N1 приложенной в точке A1.

Уравнения движения колеса запишутся в виде системы:

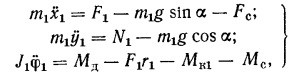
Где x1, y1 – координаты положения оси колеса O1; Ф1 – угол поворота ведущего (заднего) колеса; “a” – угол наклона поверхности дороги к горизонтали.

Если колесо катится без проскальзывания, то x1=r1Ф1; y1=0; N1=m1g*cos”a”. Сила трения F1 без учёта сил аэродинамического сопротивления

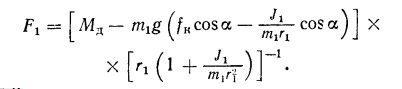
Движущий момент Mд в правой части уравнения может принимать различные значения, но если правая часть уравнения станет больше, чем fmax N1, то появится проскальзывание колеса относительно дороги и увеличение Mд оказывается нецелесообразным. Максимальное ускорение составляет величину

Характерно, что под уклон (“a”<0) можно обеспечить движение без проскальзывания с большими ускорениями.