ЛР № 5. Исследование объемного резонатора.
1. Цель работы: Иметь навыки исследования и расчета параметров объемных резонаторов
2. Содержание работы
1. Исследовать
зависимость частоты объемного резонатора
в виде отрезка прямоугольного волновода
сечением а
b
от перемещения поршня l
для перестройки резонатора. В резонаторе
существует тип колебания Н, Е. Исходные
данные по вариантам приведены в
индивидуальных заданиях 1.
2. Расчет конструкции цилиндрического объемного резонатора. Определить диаметр цилиндрического объемного D резонатора длиной l выходного каскада передатчика радиорелейной станции связи Р-414, чтобы резонансная частота возбуждаемых в нем колебаний типа Н была равна f. Исходные данные по вариантам приведены в индивидуальных заданиях 2.
3. Расчет параметров объемного резонатора. Определить добротность и резонансную частоту цилиндрического объемного резонатора тропосферной станции связи диаметром D и длиной l, в котором будут возбуждаться колебания типа H. Стенки резонатора изготовлены из меди проводимостью γ. Исходные данные по вариантам приведены в индивидуальных заданиях 3.
4.
Резонатор передающего тракта
тропосферной станции связи Р-404М имеет
размеры: а
b
l,
заполнен диэлектриком с параметрами
и
.
Материал стенок – медь с проводимостью
.
Найти резонансную частоту, добротность
и полосу пропускания резонатора на типе
колебаний Н, Е.
Исходные данные по вариантам приведены в индивидуальных заданиях 4.
5. Экспериментальное определение добротности объемного резонатора СВЧ генератора на различных частотах его генерирования. Исходные данные по вариантам приведены в индивидуальных заданиях 5.
3. Основные теоретические сведения
1. Резонансная частота и длина собственных
колебаний типа
и
в прямоугольном объемном резонаторе
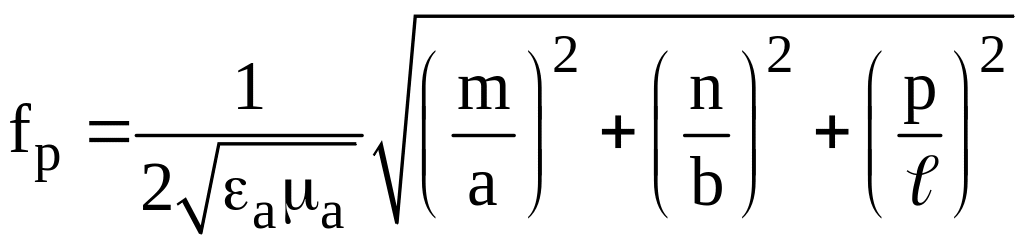, (1)
.
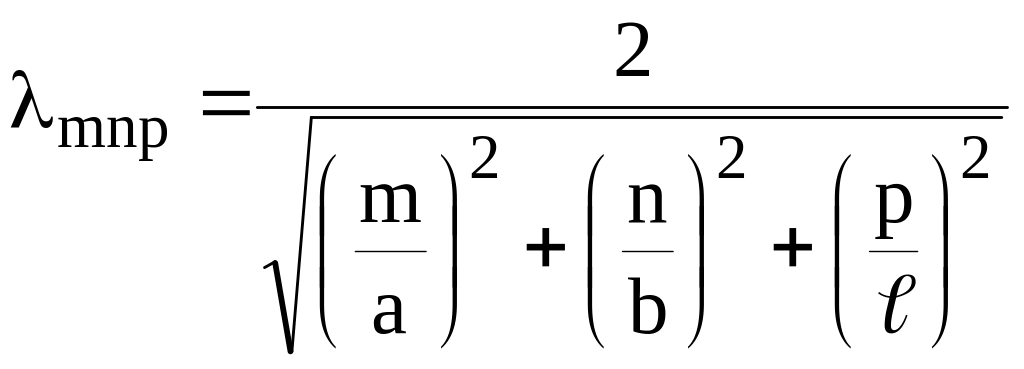(2)
где
– геометрические размеры резонатора;
– индексы, cоответствующие
типу колебания (
или
);
– абсолютная диэлектрическая и магнитная
проницаемости вещества, заполняющего
резонатор.
В
прямоугольном резонаторе низшими могут
быть колебания типов
,
и
,
у которых один из индексов равен нулю,
а два других - единице. Основным является
колебание Н или Е, у которого значение
наибольшее.
2. Резонансная частота колебаний в цилиндрическом резонаторе типа
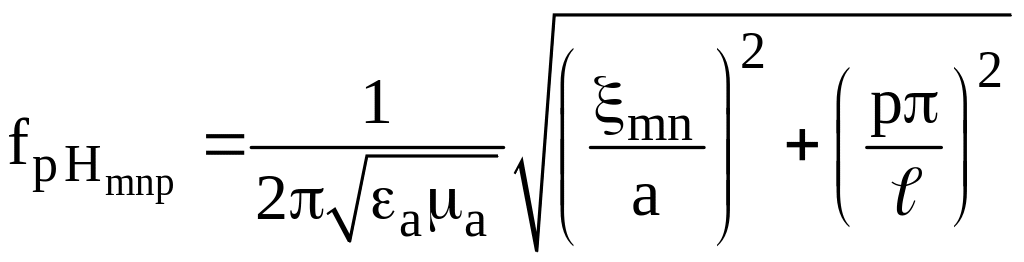, (3)
типа
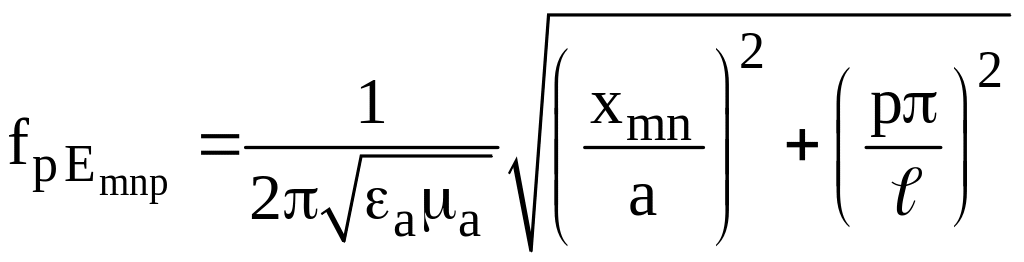, (4)
где
а и
– радиус и длина объемного резонатора;
– n-й корень m-го
порядка, при котором функции Бесселя
m-го порядка
(таблица 1);
– n-й корень m-го
порядка, при котором производная функции
Бесселя первого родя m-го
порядка
(таблица 2); p – индекс,
определяющий число вариаций поля вдоль
объемного резонатора.
Таблица 1
-
n
m=0
m=1
m=2
m=3
1
2,405
3,832
5,136
6,380
2
5,520
7,016
8,417
9,761
3
8,654
10,173
11,620
13,015
Таблица 2
-
n
m=0
m=1
m=2
m=3
1
3,832
1,841
3,054
4,201
2
7,016
5,332
6,705
8,015
3
10,174
8,536
9,965
11,344
Основным колебанием
типа Е в цилиндрическом резонаторе
является
,
основным колебанием типа Н -
.
3. Добротность объемных резонаторов:
для колебаний типа в прямоугольном резонаторе
, (5)
для колебаний типа
в цилиндрическом резонаторе
, (6)
для колебаний типа
в цилиндрическом резонаторе
, (7)
для колебаний типа в цилиндрическом резонаторе
. (8)
Инженерная формула определения добротности
. (9)
(Для
цилиндрического резонатора
,
4. Добротность объемного резонатора, заполненного диэлектриком с потерями
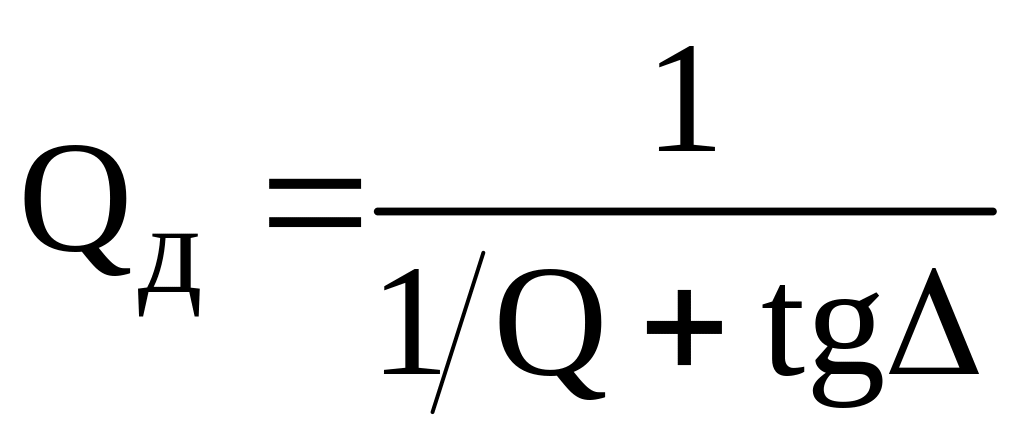, (10)
где
- добротность резонатора, обладающего
лишь потерями металлических стенок.
5. Полоса пропускания объемного резонатора
.
(11)
6. Тангенс угла потерь
(12)
7. Глубина
проникновения
8.
Поверхностное сопротивление
Приложения
Таблица1 – Физические постоянные
