Аджемян Лоран Цолакович

д.т. (812) 428-25-72, м.т. 8-921-778-26-21

Loran.Adzhemyan@pobox.spbu.ru

УДК 536.423.4+531.528

ПЕРЕКОНДЕНСАЦИЯ ПЕРЕСЫЩЕННОГО ПАРА: АНАЛИТИЧЕСКИЕ ТЕОРИИ И ЧИСЛЕННЫЙ ЭКСПЕРИМЕНТ

А.Н.Васильев, А.К.Казанский, Л.Ц.Аджемян

Санкт-Петербургский государственный университет,

физический факультет

198504 Санкт-Петербург, Петродворец, ул. Ульяновская, 1

Поступила в редакцию

Численным интегрированием уравнений движения изучен процесс конденсации пересыщенного пара с момента окончания образования зародышей и до достижения асимптотического режима переконденсации. Проведена проверка аналитических теорий конденсации. Изучена зависимость финального автомодельного распределения капель по размерам от вида их начальной функции распределения в широком диапазоне изменения параметров.

КОНДЕНСАЦИЯ ПЕРЕСЫЩЕННОГО ПАРА ПО ОКОНЧАНИИ СТАДИИ ОБРАЗОВАНИЯ НОВЫХ ЗАРОДЫШЕЙ

Процесс конденсации пересыщенного пара по окончании стадии образования новых зародышей (капель) описывается системой уравнений для радиуса капли , функции распределения капель по размерам, числовой плотности пересыщенного параи связанного с ней соотношением

, (1)

критического радиуса капель. Здесь– плотность насыщенного пара над плоской границей раздела фаз, параметропределен соотношением, где– коэффициент поверхностного натяжения,– плотность жидкости. Соответствующая система уравнений имеет вид [1]:

, (2)

,, (3)

(4)

Уравнение (2) описывает изменение со временем радиуса капли в диффузионном режиме поглощения каплей пара, здесь – коэффициент диффузии. Уравнение (4) представляет собой условие постоянства полного числа молекул в единице объема(пар + капли). Функция распределениянормирована так, что интеграл

(5)

дает среднее количество капель в единице объема. Дифференцируя (5) по времени, используя уравнение движения (3) и интегрируя по частям, получаем соотношение

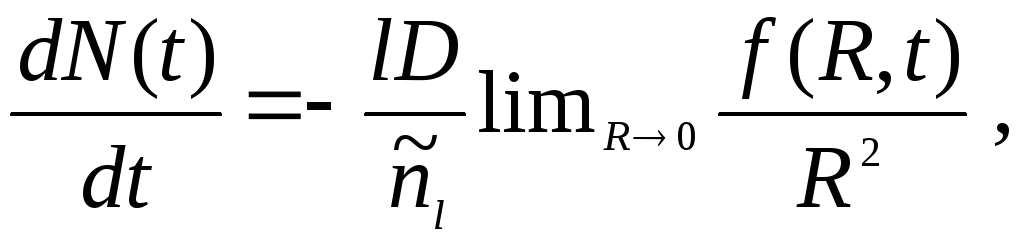(6)

определяющее скорость убыли числа капель. Чтобы она была конечна, необходимо, чтобы функция распределения при малых имела асимптотику

. (7)

В начале стадии конденсации пересыщение заметно превышает единицу и критический радиус в (2) является малой величиной порядка(например, для водысм.). Мы будем считать, что в начальном распределениипредставлены капли существенно большего размера. В этом случае в начальной стадии вторым слагаемым в уравнении (2) можно пренебречь и уравнение (3) для функции распределения имеет явное решение, которое выглядит наиболее просто, если его сформулировать в терминах распределения по квадрату радиуса капли– это распределение сохраняет свою первоначальную форму, смещаясь по времени в сторону больших размеров капель. Такой процесс мог бы продолжаться до тех пор, пока не будет исчерпан запас избыточного пара, однако он сопровождается ростоми при достаточном падении пересыщения критический радиус “догоняет” по величине основную массу капель – начинается процесс переконденсации. Второе слагаемое в (2) становится существенным: капли с размером больше критического продолжают расти, с размером меньше критического – уменьшаться в размерах.

В основополагающих работах по теории переконденсации [2,3] было найдено асимптотическое поведение функции распределения на больших временах. Согласно этой теории при достаточно больших временах функция распределения забывает все детали начального распределения, она носит автомодельный характер и единственным параметром, определяющим ее зависимость от времени, является текущий критический радиус :

,, (8)

где – универсальная функция безразмерного радиуса:

(9)

Функция (8) сиз (9) является точным решением уравнения (3), если критический радиус степенным образом зависит от времени

, (10)

этому соответствует асимптотическое убывание пересыщения пара по закону

. (11)

Уравнение баланса вещества (4) выполнено приближенно, с учетом того, что подавляющая часть избыточного пара перешла к этому моменту в капли, а интеграл (4) с функцией (8) не зависит от времени, при этом постоянная в (8) выбирается из условия

(12)

откуда, с учетом (9),

(13)

В теории Лифшица-Слезова [2,3] доказана “локальная устойчивость” асимптотического решения (8)–(10), проявляющаяся в том, что если система приблизилась к данному асимптотическому режиму, то поправки к нему будут малы. Это не означает, однако, устойчивости решения по отношению к вариациям начальных данных.

Действительно, как показано в работах [4-6], функция (9) не является единственной, делающей автомодельное представление (8), (10) решением уравнения (3). Она соответствует начальным функциям , достаточно хорошо убывающим при больших, но для которых отсутствует понятие максимальной капли. Для “финитных” начальных распределений(существует максимальная капля), возможны другие варианты автомодельного решения (8), (10) (с другими функциями). В настоящей работе путем численного решения уравнений (2)-(4) мы хотели проверить, действительно ли всегда реализуется один из вариантов асимптотического решения (8), (10) и выяснить, почему для финитных распределений оказываются недействительными аргументы Лифшица-Слезова в пользу выбора универсального решения (9).

ВЫЧИСЛИТЕЛЬНАЯ ПРОЦЕДУРА

Для реализации процедуры численного решения уравнения (2)–(4) были преобразованы к более удобному виду, не содержащему размерных параметров, путем введения безразмерных переменных

, (14)

где – величина критического радиуса в начальный момент времени,

. (15)

Вторая модификация затрагивает уравнение баланса вещества (4). Сложность его использования состоит в том, что для нахождения из (4) очень малой величины пересыщения пара на фоне прочих входящих в это уравнение больших величин требуется очень высокая точность вычисления последних (поскольку они почти точно компенсируются). Мы сочли более удобной другую форму уравнения баланса вещества, которая получается из (4) дифференцированием по времени и использованием уравнений (2), (3). Принимая в качестве независимой переменной критический радиус и исключаяс помощью (1), можно записать получающееся уравнение в безразмерных переменных (14) в виде

. 16)

В этом уравнении мы перешли затем к представлению Лагранжа

(17)

заменив усреднение с функцией распределения в момент времени на усреднение с начальной функцией распределения и перебросив зависимость от времени на траектории “представляющих точек”– решения уравнения

(18)

с начальным условием . В некоторый момент времени величинаможет оказаться равной нулю, а затем перейти в отрицательную область, соответствующие вклады в среднее значение в (17) необходимо отбросить, поэтому в подынтегральное выражение введена

В качестве выбирались функции, локализованные в областиЭта область разбивалась на 10000 частейКаждая из точек разбиения служила начальным условием для траектории, совокупность которых находилась из решения уравнений (17), (18). Для ускорения расчетов временной шаг постепенно увеличивался со временем. Нами использовался также другой способ расчета – выбирались только 2000 представляющих точек, но через некоторое время исчезнувшие к этому моменту точки восстанавливались с помощью квадратичной интерполяции. Результаты расчетов обоими методами совпадают. Однако второй способ вычислений работает значительно быстрее и позволяет продвинуться дальше по времени.

По найденным траекториям функция распределения в момент временинаходилась с использованием соотношения

, (19)

где – интервал, в который перешел интервалпри движении его концов по траекториям. Правая часть (19) представляет собой число капель в интервалев начальный момент времени, левая – равное ему число капель в момент. Из (19) находим

(20)

При приближенном вычислении производная в (20) заменялась на отношение соответствующих конечных интервалов.

ОБЩИЙ ВИД АВТОМОДЕЛЬНОГО РЕШЕНИЯ

Прежде чем переходить к изложению результатов, полученных численным интегрированием уравнений, рассмотрим общий вид автомодельного решения. Подставляя автомодельный анзац (8) в уравнение (3), получаем

, (21)

где

. (22)

Чтобы решение уравнения (21), как это предполагалось, не зависело от , необходимо, чтобы не зависел отопределенный соотношением (22) параметр. Этому, в согласие с (10), отвечает степенная зависимость критического радиуса от времени

(23)

Таким образом, уравнение (21), определяющая конкретный вид автомодельного решения (8), (10), содержит произвольный параметр . Встает вопрос о возможных физических значениях этого параметра, из его определения (22) очевидно пока только, что.

При и любыхрешение уравнения (21) имеет асимптотику, прии любыхасимптотика имеет вид. Такой вид асимптотики при малыхсогласуется с (7), обеспечивая конечность скорости убыли числа капель (6), асимптотика при большихозначает, что в качестве решения можно выбирать лишь финитные функции– такие, чтопри, в противном случае не будет существовать интеграл в уравнении баланса вещества (4) .

Область допустимых значений параметра определяется полиномом

, (24)

стоящим множителем при производной в уравнении (21). Чтобы финитное решение этого уравнения было корректным, необходимо, чтобы выполнялось условие

(25)

в случае если , и обращения в нуль также и полинома в правой части (21) в случае. Полиномпри любыхимеет как минимум один вещественный корень. Учитывая, что, видно, что локальный минимумнаходится в точке, а локальный максимум – в точке. Отсюда заключаем, что этот всегда присутствующий корень отрицателен. На роль же, согласно (25), может претендовать положительный корень полинома.

На Рис.1 показаны графики в области локализации положительных корней.

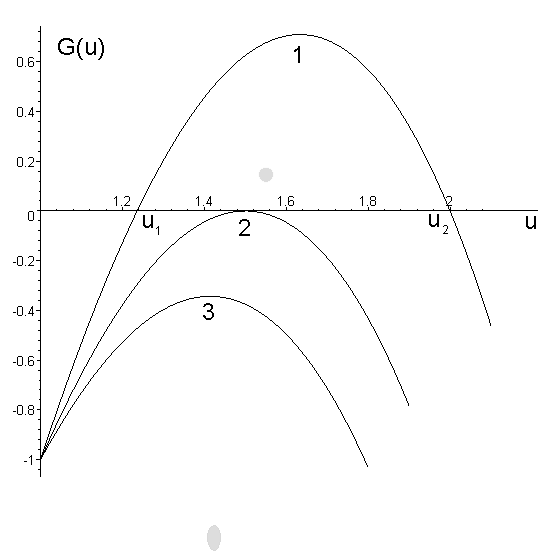Рис.1. График функции при различных значениях параметра:для кривой 3,для кривой 2,для кривой 1.

Такие корни существуют при , приони сливаются в один корень. Отметим, что для полинома (24) сумма корней равна нулю:.

Таким образом, допустимые значения параметра лежат в области. Зная корни полинома (24), нетрудно проинтегрировать уравнение (21). Результат можно представить в виде

, (26)

где . В качестве независимого параметра в решении (26) выбран показатель, прочие параметры, в том числе исходный независимый параметр, выражаются черезсоотношениями

. (27)

Для решений, удовлетворяющих условию , параметрможет лежать в диапазоне, этому соответствуют значения максимального радиуса капель в диапазоне, параметр жемонотонно убывает отпридопри. Случай, при котором(обрыв на правом краю распределения), также допустим, так как при этом полином в правой части (21) обращается в ноль в точке.

Таким образом, область физических значений параметра лежит в диапазоне, которому соответствует диапазонпараметра. Аккуратное рассмотрение предельного случаяпоказывает, что при этом (26) переходит в функцию Лифшица-Слезова (9), если учесть, что в этом случае, что приводит к появлению в (26) множителя вида, дающегов пределе.

На Рис.2 изображены графики функции (26) при различных значениях параметра .

Рис.2. Функция для трех значений параметраи функция Лифшица-Слезова.

Приведем некоторые общие свойства автомодельного распределения (26). Проинтегрируем обе части уравнения (21) в пределах от до. Интегрируя в левой части уравнения по частям и учитывая (25), получим

, (28)

откуда следует, что . Это соотношение означает равенство критического и среднего радиуса капель в автомодельном распределении при любых допустимых значениях параметра. Интеграл в правой части (28) на самом деле равен единице при выбранной нормировке функциив (26). Чтобы это доказать, надо повторить описанную процедуру интегрирования уравнения (21), разделив предварительно наобе его части, это приводит к соотношению

. (29)

Из (26) видно, что правая часть этого соотношения равна единице, с учетом (28) это показывает, что функция (26) действительно нормирована на единицу.

Приведем результаты для основных физических величин в исходных обозначениях. Для критического радиуса из (23), (14) и (15) находим

. (30)

Для числа капель в единице объема из (5), (8), (26) имеем

(31)

где - третий момент функции(26). Как уже отмечалось, средний размер капельимеет то же асимптотическое выражение, что и критический размер, т.е. описывается соотношением (30) . Уравнение (16) позволяет найти малое отличие этих величин. В размерных переменных это уравнение, с учетом (14), (15), может быть переписано в виде

, (32)

откуда, используя (30), (31), находим

. (33)

Амплитуды в асимптотических выражениях (30), (31) и (33) плавно зависят от параметра автомодельного распределения (8), (26). Величинав (30) монотонно возрастает от значения 0,703 придо 0.763 при, а величинав (31) и (33) монотонно возрастает в этой области от 0,127 до 0,167. Отметим, что соотношение (33) показывает, что разность между величиной среднего радиуса капли и критическим радиусом, т.е. на несколько порядков меньше, чем каждый из них. Тем не менее, именно эта величина является “движущей силой”, определяющей эволюцию критического размера. Это показывает, что при численном решении уравнения (32) (точнее, его безразмерного аналога (16)) необходимо выдерживать достаточно высокую точность вычислений.

ЗАВИСИМОСТЬ АВТОМОДЕЛЬНОГО РЕШЕНИЯ ОТ НАЧАЛЬНОЙ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ

Численный расчет показывает, что в зависимости от вида начальной функции распределения на больших временах реализуется одна из автомодельных функций (26) с некоторым значением параметра . Как показано в [4,5], это значение целиком определяется поведением начальной функциив окрестности максимальной капли. Это связано с тем, что имеет место следующий “закон сохранения” : если начальная функция распределенияимела в окрестности максимального размера вид

(34)

то он сохраняется и во все последующие моменты времени:

(35)

Это означает, что такое же поведение в окрестности максимальной капли должна иметь автомодельная функция распределения, что позволяет отождествить показатель в (26) с показателем в начальном распределении (34).

Поясним происхождение соотношения (35). Подставляя в (20) асимптотику (34), получаем

(36)

Производную в (36) можно заменить ее значением в точке . Существенно, что величинане обращается в нуль ни при каких значениях времени. Рассмотрим точку, близкую к точке, и выберем в (36) точкутак, чтобы. Из (36) тогда получим

. (37)

В момент времени точкав (33) перейдет в точку, а точка- в точку. Пользуясь малостью соответствующих интервалов, можно записатьПодставляя это выражение в (37), приходим к соотношению (35) с

АРГУМЕНТЫ ЛИФШИЦА-СЛЕЗОВА О ВЫБОРЕ ПАРАМЕТРА

Представляет интерес рассмотреть, почему для финитных спектров не срабатывают аргументы Лифшица-Слезова о выборе значения параметра . Переписывая, следуя [1-3], уравнение движения (18) в терминах переменной, получим

,, (38)

где - полином (24) сиз (22). Множители при производной в правой части (38) положительны, поэтому знак производной определяется знаком полинома в правой части уравнения. В асимптотическом автомодельном режиме (8), (10) величинапринимает некоторое постоянное значение. В зависимости от этого значения имеется три варианта расположения графика полинома, которые показаны на Рис.1. В [1-3] аргументируется, что только второй из них (касание оси абсцисс) согласуется с законом сохранения вещества для систем, в которых отсутствует понятие максимальной капли. Действительно, если бы финальное состояние соответствовало кривой 3, то капли с размерами, большими(таковые, хотя бы в небольшой количестве, всегда присутствуют в системе с неограниченным спектром размеров), имея отрицательную производную в (38), скопились бы в точке. К ним добавились бы и капли из промежутка между корнями. Однако в автомодельном режиме фиксированной точкесоответствует, в силу (23), (38), неограниченно растущий размер капли, что противоречит закону сохранения вещества. Этот закон будет нарушен и в случае финального состояния, описываемого кривой 1, поскольку в нем все капли имеют отрицательную производную в (38).

Для финитных функций (26) распределение капель локализовано в области размеров от до, что не противоречит уравнению баланса вещества. Однако реализуется ли такое распределение динамически при любых параметрах начального финитного распределения? Чтобы проверить это и проследить за деталями процесса, мы, решая задачу численно, вычисляли также и величину, строили графики функциии следили за относительным расположением корней этого полинома и точки.

Если начальным ситуациям соответствовали значения (корней нет), то во всех рассмотренным нами случаях финальное автомодельное распределение возникало “бесконфликтно” - величинавозрастала во времени, в определенный момент график полиномакасался оси, но к этому моменту значениеоказывалось меньшим координаты точки касания, затем появлялись оба корняи, которые постепенно занимали свои финальные положения, а величинастановилась все ближе и ближе к корню.

Мы рассмотрели также экстремальную (видимо, не совсем реалистичную) ситуацию, когда в начальном состоянии (т.е. корниисуществуют), а значениележит между корнями. Результат расчета представлен на Рис.3 (второй график дает продолжение первого по времени).

Рис.3. Зависимость от времени минимального u₁ и максимального u₂ корня полинома и максимального размера капельu_max .

Из графиков видно, что и в этом случае автомодельное распределение реализуется. В начале процесса величина убывает, а максимальный размеррастет, в некоторый момент его величина сравнивается с большим из корней, после чегоначинает убывать, причем его величина превосходит оба корня. В определенный момент величинастановится меньшей 27/4 и корни исчезают. На правой части Рис.3 показан момент, когда эти корни вновь возникают, к этому моменту значениестановится уже меньшим координаты точки касания оси графиком полинома, тем самым не происходит “запирания” части вещества в “опасной” зоне между корнями. В дальнейшемпринимает значение, очень близкое к значению минимального корня.

Для иллюстрации приведем для рассмотренного случая графики зависимости от времени функции распределения (Рис.4), а также критического радиуса и среднего размера капель (Рис.5).

Рис.4. Функция распределения в разные моменты времени, начиная от , с шагом 0.5 по(частные значенияуказаны над пиками) .

Из Рис.4 видно, что функция распределения на начальном отрезке времени сужается и стремится занять некоторое предельное положение. Затем вступает в силу механизм переконденсации, который приводит к уширению функции и сдвигу максимума в область больших значений.

Рис.5.Зависимость от времени среднего размера капель и критического размера.

На Рис.5 показано изменение во времени среднего размера капель и критического размера. На первой стадии процесса, когда общая масса капель нарастает за счет потребления избыточного пара, рост среднего размера капель опережает относительно медленное возрастает критического размера. По мере падения пересыщения ситуация меняется – ростзамедляется, а большая разность междуиприводит к быстрому росту критического радиуса, который практически сравнивается со средним размером капель. Подчеркнем, что это происходит намного раньше, чем устанавливается окончательное автомодельное распределение. В дальнейшем на довольно значительном промежутке временииостаются практически постоянными. Это соответствует начальному этапу переконденсации, на котором функция распределения уширяется (крупные капли растут за счет маленьких), но его левый край еще не достиг нулевого размера и общее число капель практически остается неизменным. Затем наступает этап быстрого убывания общего числа капель, который сопровождается ростом среднего радиуса капель и критического радиуса (они остаются при этом практически равными друг другу), этот этап завершается в конечном счете установлением финального автомодельного распределения. Проиллюстрируем также сказанное графиком зависимости от времени номера исчезающей капли на Рис.6.

Рис.6. Номер исчезающей в момент времени капли как функция . Начальное число капель = 10000.