23

Федеральное агентство по образованию

Новосибирский технологический институт

Московского государственного университета дизайна и технологии

(филиал)

АНАЛИЗ РЫЧАЖНОГО МЕХАНИЗМА

Методические указания к выполнению контрольных работ

и расчетно-графических работ по дисциплине

«Теория механизмов и машин»

для всех специальностей

Новосибирск 2007

Разработчик доц., к.т.н. Ермолаев В.Ф.

Рецензент проф., д.т.н. Подгорный Ю.И.

Работа выполнена на кафедре механики НТИ МГУДТ (филиал)

1 СТРУКТУРНЫЙ АНАЛИЗ МЕХАНИЗМА

Рассмотрим в качестве примера плоский рычажный шестизвенный механизм (рисунок 1), параметры которого приведены в таблице 1.

Таблица 1 - Параметры плоского шестизвенного механизма

,	Направление вращения звена 1	Положение	Размеры звеньев, м
			АВ	ВC	СD	DE	EF	a	b
191	+	120o	0,06	0,140	0,120	0,080	0,160	0,080	0,04

Число степеней свободы плоских механизмов рассчитывают по формуле [1]:

, (1)

где - число подвижных звеньев, - число кинематических пар пятого класса, - число кинематических пар четвертого класса.

Для данного механизма:

К инематические пары механизма приведены на рисунке 2.

Вращательные и поступательные кинематические пары относятся к парам 5 класса (рисунок 2).

Любой плоский рычажный механизм, то есть механизм с низшими парами или парами 5 класса, состоит из механизма первого класса (входного звена с одной степенью свободы) и структурных групп звеньев с нулевой степенью подвижности (групп Ассура). Группа Ассура подчиняется формуле

или

Из последнего уравнения следует, что число подвижных звеньев может быть только четным, а число пар 5 класса кратно трем. Простейшая группа Ассура состоит из двух звеньев и трех кинематических пар. По классификации И.И. Артоболевского такие группы Ассура относятся ко второму классу или двухповодковым группам [1].

Для установления класса механизма следует разложить его на механизм первого класса и группы Ассура (рисунок 3). Рассматриваемый механизм относится ко второму классу, так как содержит только группы Ассура второго класса.

2 КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМА

Кинематический анализ – определение движения звеньев механизма по заданному движению начальных звеньев.

Графические и графоаналитические методы анализа наиболее наглядны и просты в исполнении, но неточны. Рассмотрим метод планов скоростей и ускорений, который относится к графоаналитическим методам.

Планом скоростей (ускорений) механизма называется чертеж, на котором изображены в виде отрезков векторы, равные по модулю и по направлению скоростям (ускорениям) различных точек механизма в данный момент.

Сформулируем свойства планов скоростей и ускорений:

1) векторы абсолютных скоростей (ускорений) направлены из полюса;

2) векторы, соединяющие концы векторов абсолютных скоростей (ускорений), есть векторы относительных скоростей (ускорений);

3) точки, у которых скорости (ускорения) равны нулю, расположены в

полюсе;

4) векторы относительных скоростей (полных относительных ускорений) образуют на плане скоростей (ускорений) фигуру, подобную жесткому контуру на плане механизма;

5) планы скоростей и ускорений позволяют определять величину и направление угловых скоростей и ускорений.

Для механизма, положение которого определяется углом (рисунок 1), на рисунке 4 приведен план скоростей, а на рисунке 5 – план ускорений.

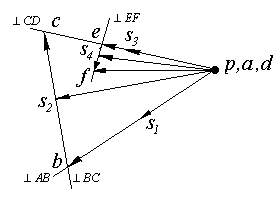
Рисунок 4 – План скоростей шестизвенного рычажного механизма ( ).

Входное (ведущее) звено АВ совершает вращательное движение c постоянной угловой скоростью , модуль скорости точки В определяется по формуле:

. (2)

На поле чертежа произвольно выбирается точка - полюс плана скоростей (рисунок 4). Из точки откладывается произвольной длины отрезок в мм (в соответствии с рисунком 4 ) перпендикулярный АВ и направленный в сторону вращения АВ. Точка А звена АВ неподвижна и будет находиться в полюсе плана. Масштаб плана скорости определяется как

.

В плоскопараллельном движении скорость точки С определяется из системы уравнений:

(3)

Относительные скорости и направлены перпендикулярно звеньям ВС и CD. Точка D звена CD неподвижна и будет находиться в полюсе плана скоростей. Через точку плана скоростей проводим прямую перпендикулярно звену ВС, а через полюс проводим прямую перпендикулярно звену CD. Точка пересечения этих прямых будет являться вектором абсолютной скорости точки С, а отрезок в масштабе будет являться вектором скорости . Отрезок будет являться вектором относительной скорости .Модули скоростей и определятся как

Скорость точки Е определяется на основании свойств подобия (векторы относительных скоростей образуют на плане скоростей фигуру, подобную жесткому контуру на плане механизма), для чего отрезок на плане скоростей разбивается пропорционально отрезкам СЕ и ЕD на плане механизма:

, откуда . Модуль скорости точки Е определится как

Скорость точки F определяется из следующего уравнения:

. (4)

Скорость при поступательном движении параллельна направляющим ползуна, а относительная скорость направлена перпендикулярно звену EF. Скорость точки F определяется в соответствии с уравнением (4): из точки проводится прямая перпендикулярно звену EF, а из полюса прямая параллельно направляющим ползуна. Точка пересечения этих двух прямых и будет концом вектора скорости точки F, а отрезок в масштабе будет вектором . Отрезок будет являться вектором относительной скорости . Модули скоростей и определятся как

Скорости центров масс звеньев определяются на основании свойств подобия (свойство планов скоростей и ускорений пункт 4). Например, скорость центра масс звена 2 будет являться вектором ,проведенным из полюса к середине отрезка :

Аналогично определяются скорости центров масс других звеньев.

Построение плана ускорений (рисунок 5) производится в следующей последовательности. Ускорение точки В определится из следующего уравнения:

(5)

Нормальное ускорение точки В направлено по звену АВ к центру вращения А, а его модуль определится по формуле:

(6)

Ведущее звено АВ вращается с постоянной угловой скоростью , тогда его угловое ускорение равно нулю. Тангенциальное ускорение точки В определяется по формуле , и также равно нулю. На поле чертежа произвольно выбирается точка - полюс плана ускорений. Из точки откладывается произвольной длины отрезок в мм (в соответствии с рисунком 5 ) параллельно АВ и направленный от точки В к точке А. Точка А звена АВ неподвижна и будет находиться в полюсе плана. Тогда в соответствии с уравнением (6) полное ускорение точки В равно его нормальному ускорению: = . Масштаб плана ускорения определяется как

В плоскопараллельном движении ускорение точки С определяется из системы уравнений:

(7)

Нормальные ускорения точки С и направлены из точки С параллельно звеньям ВС и СD, а тангенциальные ускорения и - перпендикулярно звеньям ВС и СD. Модули нормальных ускорений точки С определяются по формулам:

Ускорение точки D равно нулю. Последовательность графических построений по уравнениям (7) приведена на плане ускорений (рисунок 5). Вначале из точек и плана ускорений откладываются отрезки и , из концов которых проводятся линии действия тангенциальных ускорений и . Точка пересечения этих линий и будет концом вектора абсолютного ускорения . Линия - план ускорений звена 2, а линия - план ускорений звена 3.

Ускорение точки Е определяется также на основании свойств подобия отрезков на плане ускорений и жестких контуров на кинематической схеме механизма: , откуда отрезок . Модуль ускорения точки Е определится как

Ускорение точки F определяется из следующего уравнения:

. (8)

Ускорение при поступательном движении параллельно направляющим ползуна. Нормальное ускорение направлено из точки F параллельно звену EF. Модуль вектора определяется по формуле

.

Последовательность построений по уравнению (8) на плане ускорений: из полюса проводится линия параллельно направляющим ползуна, а из точки проводится линия параллельно звену 4, вдоль которой (от точки F к точке Е) откладывается отрезок . Так как отрезок , изображающий вектор , мал по сравнению с другими, то им можно пренебречь, и линия действия проводится из точки .Точка пересечения этих линий будет концом вектора абсолютного ускорения .

Ускорение центров масс звеньев 2, 3 и 4 определяются также как и их скорости из свойств подобия.

По планам скоростей и ускорений определяются также угловые скорости и угловые ускорения звеньев:

.

Для определения направления угловой скорости, например, звена 2, вектор (вектор относительной скорости точки С при вращении звена 2 вокруг точки В) переносится мысленно с плана скоростей в точку С звена 2 на плане механизма ( направлено против часовой стрелки или его направление положительное). Аналогично определяется направление по вектору относительного тангенциального ускорения ( направлено также против часовой стрелки или имеет положительное направление).

3 СИЛОВОЙ АНАЛИЗ МЕХАНИЗМА

Задачей силового анализа механизма является определение реакций в кинематических парах механизма и уравновешивающих сил или моментов при известных внешних силах и заданном законе движения ведущих звеньев.

При решении задачи силового анализа механизмов используется принцип Даламбера, согласно которому звено механизма может рассматриваться как находящееся в равновесии, если ко всем внешним силам, действующим на него, добавить силы инерции. Уравнения равновесия в этом случае называют уравнениями кинетостатики.

1. Определение сил, действующих на звенья механизма

3.1.1 Определение сил тяжести звеньев

Силы тяжести звеньев рычажного типа определяются по формуле

, (9)

где - масса звена; - ускорение свободного падения.

Масса звеньев рычажного типа задается зависимостью:

, (10)

где - масса звена, кг; - длина звена, мм; - коэффициент, величина которого задается преподавателем в пределах от 0,001 до 0,003 кг/мм.

Масса ползуна задается как

,

где j – любое целое число, задаваемое преподавателем.

Силы полезного сопротивления прикладываются к ползунам, направляются в сторону противоположную их движению, численное значение задается в двадцать раз больше силы тяжести звена АВ.

Для рассматриваемого механизма принимаем и 3, тогда

(Н);

(Н).

Аналогично определяются силы тяжести других звеньев. Результаты расчета сил тяжести приведены в таблице 2.

Таблица 2 - Результаты расчета сил тяжести

1,8	4,2	3,6	4,8	5,4	36