
Самостоятельная работа № 4
“Функции нескольких переменных”
ЗАДАНИЕ
1. Найти
![]() и
и
![]() функции:
функции:
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17. |
18. |
19. |
20. |
21. |
22. |
23. |
24. |
25. |
26. |
27. |
28. |
29. |
30. |
ЗАДАНИЕ № 2. Найти и функции:
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17. |
18. |
19. |
20. |
21. |
22. |
23. |
24. |
25. |
26. |
27. |
28. |
29. |
30. |
ЗАДАНИЕ 3. Показать, что
1. |
|
2. |
для
функции
|
3. |
для
функции
|
4. |
|
5. |
для
функции
|
6. |
для
функции
|
7. |
для
функции
|
8. |
|
9. |
|
10. |
для
функции
|
11. |
для
функции
|
12. |
|
13. |
для
функции
|
14. |
|
15. |
|
16. |
|
17. |
для функции . |
18. |
для функции |
19. |
для функции . |
20. |
для функции . |
21. |
для функции . |
22. |
для функции |
23. |
для функции . |
24. |
для функции . |
25. |
для функции . |
26. |
для функции . |
27. |
для функции . |
28. |
для функции . |
29. |
для функции . |
30. |
для функции . |
ЗАДАНИЕ 4. Исследовать на экстремум:
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17. |
18. |
19. |
20. |
21. |
22. |
23. |
24. |
25. |
26. |
27. |
28. |
29. |
30. |
ЗАДАНИЕ 5. Найти наибольшее и наименьшее значения функции:
1. |
|
2. |
|
3. |
|
4. |
|
5. |
|
6. |
|
7. |
|
8. |
|
9. |
|
10. |
|
11. |
в области, ограниченной прямыми
|
12. |
|
13. |
|
14. |
|
15. |
|
16. |
|
17. |
в треугольнике со сторонами . |
18. |
в треугольнике со сторонами . |
19. |
в замкнутой области, ограниченной и осью . |
20. |
в треугольнике со сторонами . |
21. |
в треугольнике со сторонами |
22. |
в замкнутой области, ограниченной и осью . |
23. |
в квадрате |
24. |
в квадрате |
25. |
в замкнутой области, ограниченной линиями и |
26. |
в области, ограниченной прямыми |
27. |
в области, ограниченной прямыми |
28. |
в прямоугольнике, ограниченном прямыми
|
29. |
в треугольнике со сторонами |
30. |
в треугольнике со сторонами |
ЗАДАНИЕ 6. Найти производную функции:
1. |
|
2. |
|
3. |
|
4. |
|
5. |
|
6. |
|
7. |
|
8. |
|
9. |
в точке (3; 1) по направлению вектора . |
10. |
в точке (1; 1) в направлении биссектрисы 1-го координатного угла. |
11. |
|
12. |
|
13. |
|
14. |
|
15. |
|
16. |
|
17. |
в точке (3; 1) в направлении от этой точки к точке (6; 5). |
18. |
в точке (1; 1) в направлении биссектрисы 1-го координатного угла. |
19. |
в точке (2; 1) в направлении от этой точки к началу координат. |
20. |
в точке (1; 1) в направлении луча, образующего угол в 60о с осью ОХ. |
21. |
в начале координат в направлении луча, образующего угол в 30о с осью OX. |
22. |
в точке (1; 3) по направлению вектора . |
23. |
в точке (1; 2) в направлении, составляющем с осью OX угол в 60о. |
24. |
в точке (1; 2) в направлении вектора, образующего с осью OX угол в 45о. |
25. |
в точке (3; 1) по направлению вектора . |
26. |
в точке (1; 1) в направлении биссектрисы 1-го координатного угла. |
27. |
в точке (1; 2) в направлении от этой точки к точке (1; 1). |
28. |
в точке (1; 1) в направлении, образующем углы α = 30о, β = 60о. |
29. |
в точке (4; 1) в направлении от этой точки к точке (5; 1). |
30. |
в точке (5; 1) в направлении от этой точки к точке (9; 4). |
Образец выполнения самостоятельной работы







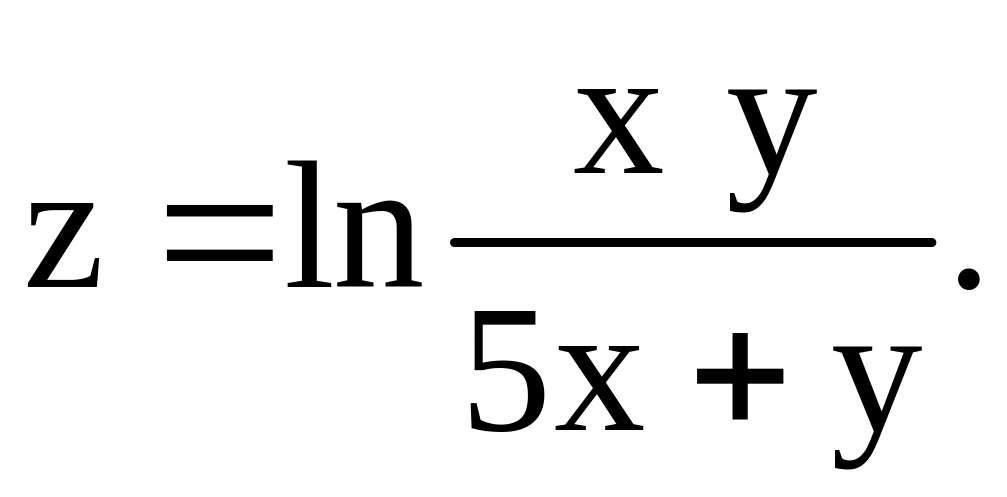




 для
функции
для
функции
 для
функции
для
функции
 .
. .
. .
. для
функции
для
функции
 для
функции
для
функции
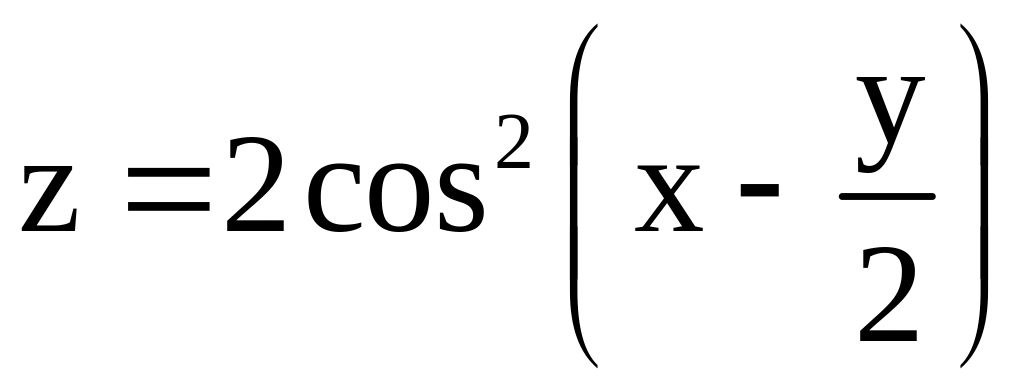 .
. для
функции
для
функции
 .
. для
функции
для
функции
 для
функции
для
функции
 .
. для
функции
для
функции
 .
. и
и
 в точке (1; 1) в направлении луча,
образующего угол в 60о с осью
ОХ.
в точке (1; 1) в направлении луча,
образующего угол в 60о с осью
ОХ.