Примеры выполнения заданий

1. Множества и отношения Задание 1

Пример 1:

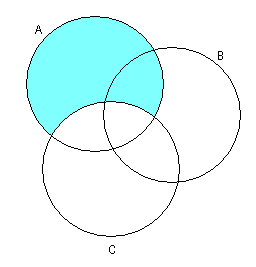
1)

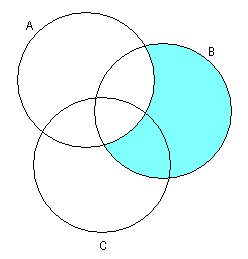
2)

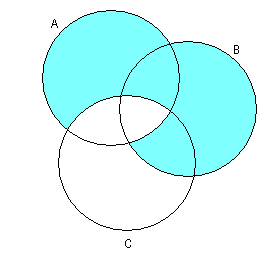
3)

Пример 2:

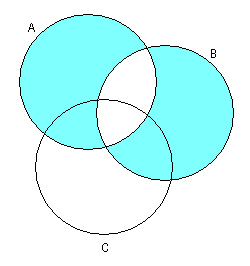
1)

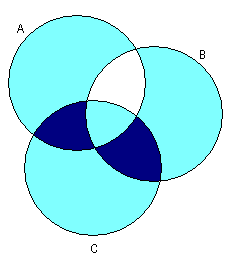
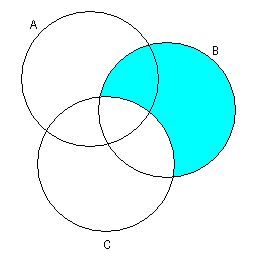
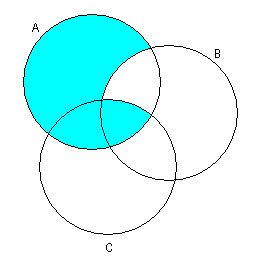
2)

3)

Задание 2

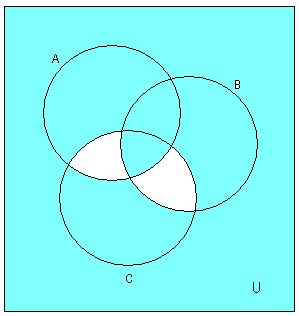
Покажем выполнение равенства на диаграммах Эйлера-Венна.

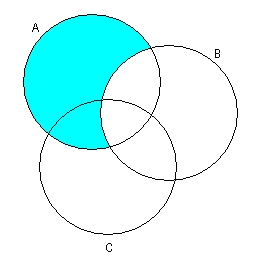
1) Левая часть равенства:

2) Правая часть равенства:

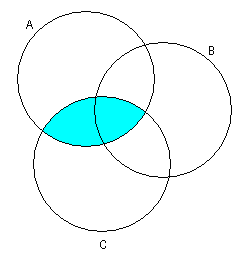
Докажем при помощи тождеств алгебры множеств:

Задание 4

Схематично изобразить геометрическое место точек прямого произведения {1,2,3,4}×{xx-точка квадрата}.

Геометрическое место точек прямого произведения множеств {1,2,3,4}×{xx-точка квадрата} изображено на рисунке.

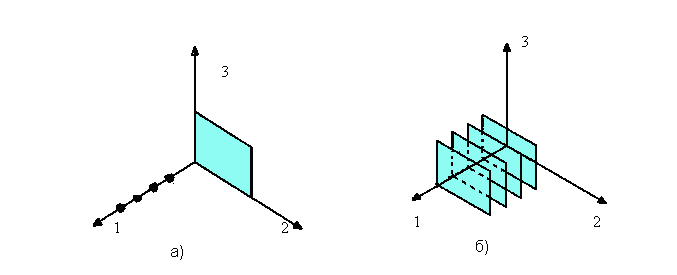
На рисунке а) на оси 1 изображены точки множества {1,2,3,4}; на плоскости 2О3 – множество точек квадрата: {xx-точка квадрата}.

На рисунке б) изображен результат.

Задание 6

,

a) = {<1,1>, <1,2>, <2,1>, <2,2>, <2,3>, <3,1>, <3,6>, <4,3>, ...}

b)

c) Несимметрично, т.к. для пары <3,1> не существует пары <1,3>;

Рефлексивно, т.к. для найдется пара <x,x>. Например, <1,1>, <2,2>, <3,3> и т.д.;

Не транзитивно, т.к. для пар <1,2> ,<2,3> не существует пары <1,3>;

Не антисимметрично, т.к. есть пары <1,2>, <2,1> и при этом 1 2.

Задание 7

«Быть подмножеством» на семействе множеств

антисимметрично, т.к. из того, что , а следует, что ;

несимметрично, т.к. из того что , не следует, что ;

рефлексивно, т.к. любое множество ;

транзитивно, т.к. из того, что , а следует, что .

2. Теория графов Задание 1

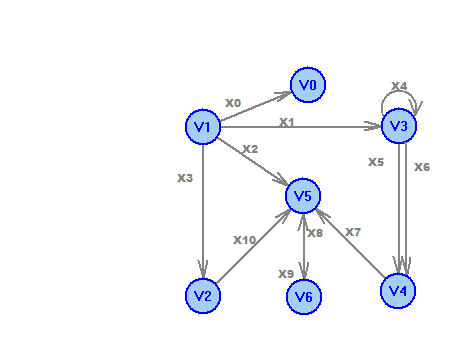
1. Ориентированный псевдограф D=(V,X). V={v₀,v₁,v₂,v₃,v₄,v₅,v₆}, X={x₀,x₁,x₂,x₃,x₄,x₅,x_6,x₇,x₈,x₉,x₁₀}. x₀=<v₁,v₀>, x₁=<v₁,v₃>, x₂=<v₁,v₅>, x₃=<v₁,v₂>, x₄=<v₃,v₃>, x₅=<v₃,v₄>, x₆=<v₃,v₄>, x₇=<v₄,v₅>, x₈=<v₆,v₅>, x₉=<v₅,v₆>, x₁₀=<v₂,v₅>.

2. x₄ – петля, x₅,x₆ – кратные ребра, v₀ – висячая вершина.

3. Полустепени вершин: ⁺(v₀)=0, ^-(v₀)=1, ⁺(v₁)=4, ^-(v₁)=0, ⁺(v₂)=1, ^-(v₂)=1, ⁺(v₃)=3, ^-(v₃)=2, ⁺(v₄)=1, ^-(v₄)=2, ⁺(v₅)=1, ^-(v₅)=4, ⁺(v₆)=1, ^-(v₆)=1.

Матрица смежности

	v0	v1	v2	v3	v4	v5	v6
v0	0	0	0	0	0	0	0
v1	1	0	1	1	0	1	0
v2	0	0	0	0	0	1	0
v3	0	0	0	1	2	0	0
v4	0	0	0	0	0	1	0
v5	0	0	0	0	0	0	1
v6	0	0	0	0	0	1	0

Матрица инцидентности

	x0	x1	x2	x3	х4	х5	х6	х7	x8	x9	x10
v0	-1	0	0	0	0	0	0	0	0	0	0
v1	1	1	1	1	0	0	0	0	0	0	0
v2	0	0	0	-1	0	0	0	0	0	0	1
v3	0	-1	0	0	±1	1	1	0	0	0	0
v4	0	0	0	0	0	-1	-1	1	0	0	0
v5	0	0	-1	0	0	0	0	-1	-1	1	-1
v6	0	0	0	0	0	0	0	0	1	-1	0

Матрица связности:

	v0	v1	v2	v3	v4	v5	v6
v0	1	0	0	0	0	0	0
v1	0	1	0	0	0	0	0
v2	0	0	1	0	0	0	0
v3	0	0	0	1	0	0	0
v4	0	0	0	0	1	0	0
v5	0	0	0	0	0	1	1
v6	0	0	0	0	0	1	1

Матрица достижимости:

	v0	v1	v2	v3	v4	v5	v6
v0	1	0	0	0	0	0	0
v1	1	1	1	1	1	1	1
v2	0	0	1	0	0	1	1
v3	0	0	0	1	1	1	1
v4	0	0	0	0	1	1	1
v5	0	0	0	0	0	1	1
v6	0	0	0	0	0	1	1

5. Простой цикл: v₆х₈v₅х₉v₆

Цикл: нет

Простая цепь : v₁х₃v₂х₁₀v₅

Цепь: v₁х₁v₃х₄v₃х₆v₄