Лабораторне практичне заняття №7

Тема заняття: Перевірка статистичної гіпотези про рівність середніх двох вибіркових сукупностей

Мета заняття: Освоєння статистичного інструментарію перевірки гіпотез про оцінку параметрів вибіркового розподілу

Основні завдання практичного заняття:

• визначення мети перевірки гіпотез про рівність середніх двох вибіркових сукупностей;

• вивчення принципів побудови та схеми перевірки гіпотез;

• приклади перевірки гіпотез.

Методичні вказівки.

Перевірка статистичної гіпотези передбачає послідовне виконання таких етапів:

1. Оцінка вихідної інформації і опис статистичної моделі вибіркової сукупності.

2. Формулювання нульової і альтернативної гіпотез.

3. Встановлення рівня значущості, за допомогою якого контролюється помилка І роду.

4. Вибір найбільш потужного критерію для перевірки нульової гіпотези.

5. Розрахунок за певним алгоритмом фактичного зна­чення критерію.

6. Визначення критичної області і області згоди з нульовою гіпотезою, тобто встановлення табличного значен­ня критерію.

7. Співставлення фактичного і табличного значень критерію і формулювання висновків за результатами перевірки нульової гіпотези.

Приклад 7.1.

Перевірка гіпотези відносно двох середніх. Вибірки незалежні з рівними чисельностями ( ) і рівними дисперсіями в генеральних сукупностях ( )

• У приміському держгоспі досліджується раціон з добавкою вітамінів при відгодівлі тварин. Були організовані дослідна і контрольна група по 5 голів у кожній групі. Протягом місяця дослідна група тварин отримала понад звичайного раціону комплекс вітамінів. В кінці місяця для кожного виду визначено приріст у живій масі. Дані досліду подані у табл. 7.1.

Співставлення середніх добових приростів по двох групах тварин показує, що більш високий добовий приріст дали тварини дослідної групи. Однак, у зв'язку з тим, що чисельність вибірок невелика (п = 5), не виключена можливість, що розходження між добовими приростами отри­мані в результаті дії випадкових причин.

Потрібно статистично оцінити різницю між серед­німи по двох групах тварин.

За результатами перевірки гіпотези зробити висно­вок про те, що різниця між середніми лежить у межах випадкових коливань, або ж ця різниця настільки значна, що не узгоджується з нульовою гіпотезою про випадковий характер відмінностей між середніми.

Таблиця 7.1.

Добовий приріст живої маси відгодівельного поголів'я, г

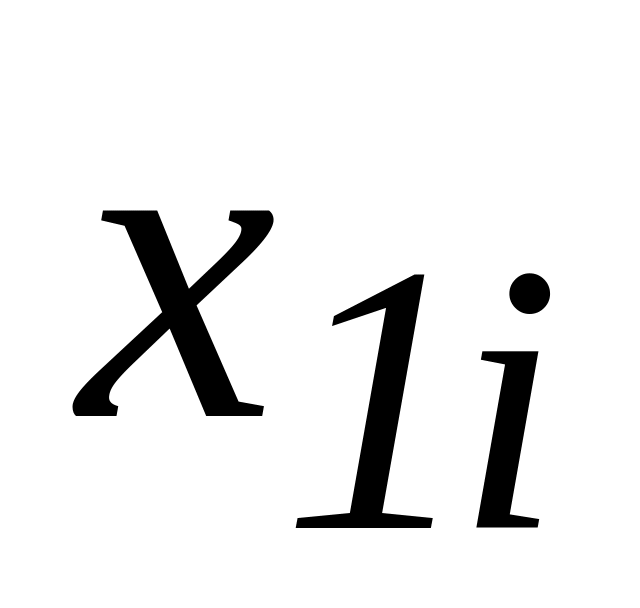
Тварини	Основний раціон + вітаміни (дослід)	Основний раціон (контроль)
1	632	520
2	691	586
3	570	490
4	694	609
5	683	590

Якщо буде доведено друге положення і відхилене перше, можна стверджувати, що умови росту тварин дослідної гру­пи істотно відрізнялись від умов росту тварин контрольної групи, тобто комплекс вітамінів стимулював підвищення до­бових приростів.

Розв'язування:

Умова задачі припускає, що обидві вибірки взяті із нор­мально розподіленої генеральної сукупності. Формування груп випадкове (незалежне), тому оцінюватись повинна різниця між середніми. В середовищі Excel створюємо форму вихідних даних.

Визначимо середні добові прирости у дослідній і конт­рольній групах за допомогою вбудованої функції СРЗНАЧ(), параметри якої є масиви даних відповідних вибірок. Так, в рядку 8 отримуємо середні значення, в рядку 9 обчислимо фактичну різницю між середніми (Рис.7.1). Істотність цієї різниці повинна бути оцінена Дія цього необхідно перевірити гіпотезу про рівність двох середніх.

Р ис.7.1. Обчислення середніх та їх різниці

Етапи схеми перевірки гіпотези:

1. Сформулюємо нульову Но і альтернативну Н_а гіпотези:

.

2. Приймемо рівень значущості =0,05, гарантуючи прийняття гіпотези або відмови від неї з ймовірністю по­милки тільки в 5 випадках із 100.

3. Найбільш потужним критерієм для перевірки такої гіпотези Но є -критерій Стьюдента.

4. Сформулюємо правило прийняття рішення за ре­зультатами перевірки Н_а. Оскільки за альтернативною гі­потезою може бути або більше або менше , то крити­чна область повинна бути встановлена з двох сторін: (так звана двостороння критич­на область завдання критерію).

Критична область при =0,05 буде міститися в ме­жах - всі значення вищі, ніж верхнє 2,5% і нижче, ніж 2,5% точки розподілу -критерію Стьюдента.

Висновок при перевірці Н₀ можна сформулювати та­ким чином: гіпотеза Но відхиляється, якщо вибіркове зна­чення критерію виявиться в критичній області, тобто якщо . В протилежному випадку Н₀ повинна бути прийнята.

5. Щоб перевірити Н₀, потрібно визначити фактичне значення -критерію Стьюдента і порівняти його з таблич­ним значенням.

Фактичне значення -критерію Стьюдента визначимо за формулою:

,

де - середнє значення ознаки за першою виборкою (серед­ній добовий приріст за даними дослідної групи); - середнє зна­чення ознаки за другою виборкою (середній добовий приріст за даними контрольної групи); і - середнє значення ознаки відповідних генеральних сукупностей, з яких зроблені вибірки (оскільки згідно з Н₀: , то ); - узагальнена середня помилка різниці середніх.

Для визначення фактичного значення -критерію Стьюдента зробимо такі обчислення.

6. Обчислимо за кожною вибіркою скореговані на втрату ступенів свободи варіації дисперсії за допомогою вбудованої функції ДИСП(), параметри якої є масиви даних відповідних вибірок (рядок 10). Обчислення за вказаною функцією проводиться на основі формули: .

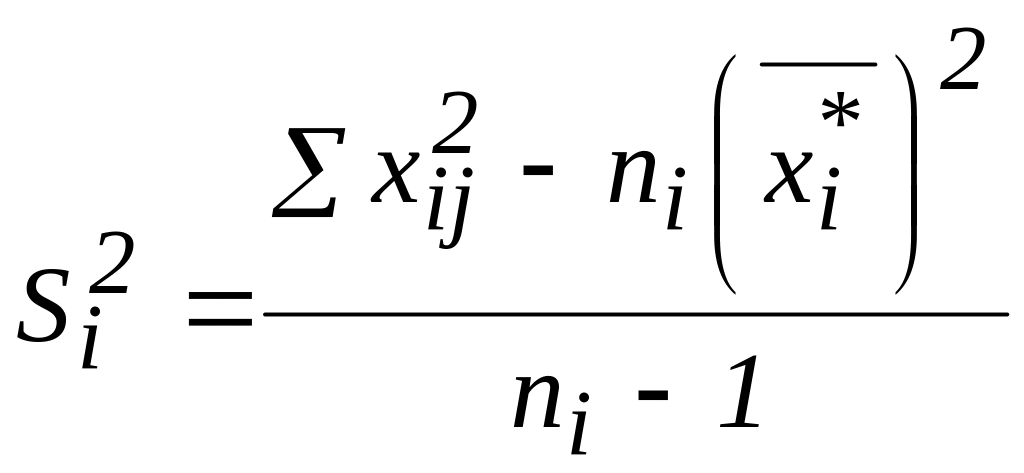7. Розрахуємо квадрати середніх помилок за кожною виборкою й узагальнену середню помилку різниці середніх (рядки 11, 12 Рис.7.2.):

8. Розрахуємо фактичне значення -критерію Стьюдента (рядок 13 Рис.7.2.):

.

9. Встановимо табличне значення -критерію Стью­дента (рядок 14 Рис.7.2.), виходячи із рівня значущості =0,05 і загально­го числа ступенів свободи для двох вибірок: за допомогою вбудованої функції СТЬЮДРАСПОБР(0,05;8): .

10. Співставимо фактичне і табличне значення t-критерію Стьюдента:

; 2,88 > 2,31.

Отже, вибіркове значення критерію зна­ходиться в критичній області, нульова гіпотеза про рів­ність середніх у генеральних сукупностях повинна бути відхилена і прийнята альтернативна гіпотеза про те, що середні в генеральних сукупностях нерівні. Таким чином, дані досліду не узгоджуються з гіпотезою про те, що відмінності в середніх приростах випадкові. Фактич­не значення t-критерію Стьюдента перевищує його можливу теоретичну величину, яка вимірює випадкове коли­вання, що дозволяє зробити висновок про істотність (вірогідність) відмінностей між середніми.

Р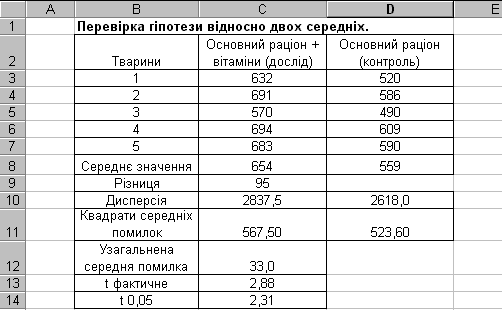 ис.7.2. Обчислення -критерію Стью­дента

Відзначимо, що проведені розрахунки можна отримати також за допомогою вбудованого пакету “Анализ данных”, який складається з набору інструментів.

П ерш за все, необхідно перевірити гіпотезу про рівність двох середніх за критерієм Фішера, використовуючи інструмент «Двухвыборочный F-тест для дисперсии». Для цього слід активізувати названий пакет Сервис/Анализ данных та обрати вказаний інструмент. На рис.7.3. зображено діалогове вікно інструменту «Двухвыборочный F-тест для дисперсии».

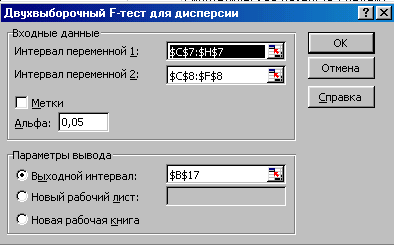
Рис.7.3. Діалогове вікно інструменту “Двухвыборочный F-тест для дисперсии ” пакету “Анализ данных”

В поле Интервал переменной 1 слід ввести діапазон даних першої виборки, в поле Интервал переменной 2 - діапазон даних другої виборки. В поле Выходной интервал вводиться посилання на клітину виведення результатів обчислень.

На рис. 7.4. представлено результат виконання інструменту “Двухвыборочный F-тест для дисперсии” пакету “Анализ данных”.

Рис. 7.4. Результат виконання інструменту “Двухвыборочный F-тест для дисперсии”

F_факт=1,084 < =6,388 - приймається гіпотеза про рівність дисперсій у генеральних сукупностях.

Для подальшого дослідження про рівність середніх слід використати інструмент “Двухвыборочный t-тест с одинаковыми дисперсиями”.

На рис. 7.5. представлено результат виконання інструменту “Двухвыборочный t-тест с одинаковыми дисперсиями” пакету “Анализ данных”. На основі представлених значень t-статистики та t-критического підтверджується висновок про відхилення нульової гіпотези про рівність середніх у генеральних сукупностях і прийняття альтернативної гіпотези про те, що середні в генеральних сукупностях нерівні.

Рис. 7.5. Результат виконання інструменту “Двухвыборочный t-тест с одинаковыми дисперсиями”

Дані для самостійного розв'язування наведені в таблиці 7.2.

Таблиця 7.2.