
![]() Независимые
циклы
Независимые
циклы
Определение
З
![]()
7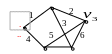
![]()
![]()
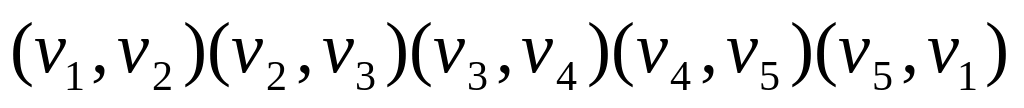

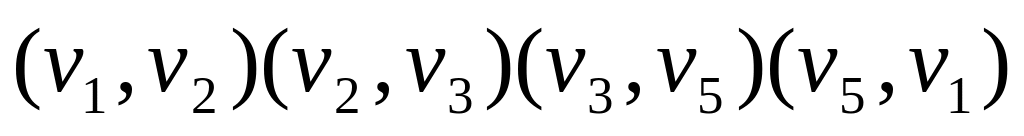
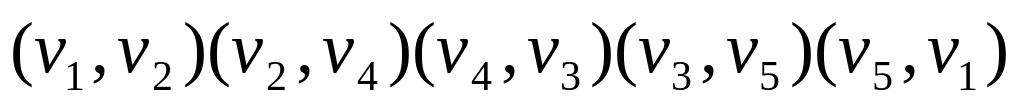 и
тд.
и
тд.
Цикл называется линейно-зависимым от некоторой совокупности других цикло, если его можно построить линейной комбинацией циклов этой совокупности. Чтобы пояснить понятие линейной комбинации, рассмотрим совокупность двух циклов приведенного графа:
1 .
2.
![]()
Произведем их обход. Исключая из обхода ребро (v3,v5), пройденное туда и обратно, получаем новый цикл

Этот цикл построен в результате линейной комбинации исходных циклов и является линейно-зависимым от них. Таким образом, непосредственно на графе получено линейное построение зависимого цикла. Приведем определение линейно комбинации циклов. Представим каждый цикл двоичным m-разрядным кодом, где m-число ребер графа. Пронумеруем ребра. Для i-ого цикла компонента Цij вектора Цi определяется следующим образом:
![]() =
=![]()
Тогда линейно комбинацией вектора Цi называется вектор, полученным сложением по модулю два двух векторов циклов.
Выполним сложение векторов циклов 1 и 2:
1 2 3 4 5 6 7 - ребра
1 1 0 1 1 0 0 – вектор
![]()
![]()
0 0 0 0 1 1 1 – Вектор
![]() -
-
![]() – результирующий вектор цикла.
– результирующий вектор цикла.
Системой независимых циклов графа называется максимальная линейно независимая совокупность циклов графа.
Цикломатическое число
![]() .
Граф в общем случае может иметь не одну
систему независимых циклов, однако
число
циклов в системе для каждого графа
определяется его структурой однозначно.
Число
называется цикломатическим числом
графа.
.
Граф в общем случае может иметь не одну
систему независимых циклов, однако
число
циклов в системе для каждого графа
определяется его структурой однозначно.
Число
называется цикломатическим числом
графа.
Теорема (Эйлера) Мощность системы независимых циклов в графе определяется формулой =m-n+p, где m – число ребер; n- число вершин; p – число компонент связности.
В примере = 7-5+1=3 т.е. в систему включаются три взаимно независимых цикла, каждый следующий цикл можно построить их линейной комбинацией.
Система независимых циклов плоского графа
Теорема. Края конечных граней плоского графа составляют систему независимых циклов.
Р
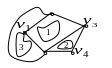
Можно предложить другое плоское изображение графа, получим другую систему независимых циклов, равную =3:
1.
2.
![]()
?
В электронике, электротехнике и системотехнике используют данную закономерность для анализа и распределениях компонент-схем.
Алгоритм построения системы независимых циклов графа
Строится произвольный остов графа. В исходном графе отмечаются ребра, включенные в остов.
Выбирается очередное неотмеченное ребро и строится цикл, содержащий это ребра и ребра остова. Такой цикл обязательно существует, так как вершины остова связаны. Рассмотренное ребро отмечается и если есть еще неотмеченное ребро, то выполняется п.2, иначе – п.3
П
о формуле Эйлера =m-n+p производится проверка числа построенных циклов.

Система циклов
=9-7+1=3
П

![]()
![]()
Система циклов
=9-7+2=4
Матрицы циклов и сечений ориентированных графов
В
![]()
![]() не входит в цикл; если же
не входит в цикл; если же
![]() ,то
=1
или
=-1
в зависимости от того, совпадают или
нет направление дуги
с выбранным направлением обхода графа
и построения цикла.
,то
=1
или
=-1
в зависимости от того, совпадают или
нет направление дуги
с выбранным направлением обхода графа
и построения цикла.
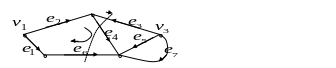
![]()
![]()
![]()
|
|
|
|
|
|
|
-1 |
1 |
0 |
1 |
0 |
-1 |
0 |
Максимальное линейно независимое множества векторов, объединенных по строкам, образуют матрицу Ц, называемую матрицей циклов графа.
Сечением (разрезом) S графа
G называется определенное
подмножество дуг, удаление которого
увеличивает число компонент связности,
так что подграф G\S
состоит из двух частей
![]() и
и
![]() (
(![]() ),
связь между которым в графе G
осуществлялась только дугами сечения
S.
),
связь между которым в графе G
осуществлялась только дугами сечения
S.
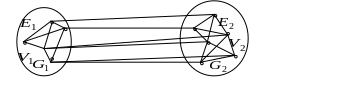
Вершины
![]() из
,
которые инцидентны дугам S,
называются первой стороной сечения;
вершины
из
,
которые инцидентны дугам S,
называются первой стороной сечения;
вершины
![]() из
,
инцидентные S – второй
стороной сечения S.
из
,
инцидентные S – второй
стороной сечения S.
Следовательно, непересекающиеся
подмножества вершин
и
,
образуют разбиение множества вершин
на классы V=![]() графа G. Для
сечения (как и для цикла) вводится
произвольная ориентация – направление
от одной стороны сечения к другой.
графа G. Для
сечения (как и для цикла) вводится
произвольная ориентация – направление
от одной стороны сечения к другой.
Вектор-сечение
![]() – это строка
,
у которой компонента
– это строка
,
у которой компонента
![]() =0,
когда дуга
не входит в сечение S. Если
дуга
принадлежит сечение согласно принятой
ориентации сечения, то
=1,
если не совпадает, то
=-1.
Примем для сечения
=0,
когда дуга
не входит в сечение S. Если
дуга
принадлежит сечение согласно принятой
ориентации сечения, то
=1,
если не совпадает, то
=-1.
Примем для сечения
![]() ,
то вектор сечение имеет вид:
,
то вектор сечение имеет вид:
|
|
|
|
|
|
|
(0 |
0 |
-1 |
1 |
0 |
1 |
0) |
=
На основе сечений можно образовать
матрицу сечений, строки которой образуют
максимальный линейно-независимый набор
векторов сечений. Столбцы матрицы
сечений и циклов нумеруются одинаково
– дугами графа, а число строк может быть
различным. Сечение S
называется фундаментальным (по древу
Т) , если оно содержит в точности одну
дугу
![]() дерева Т, а ориентация сечения S
согласована с ориентацией дуги
.
Следовательно, задание дуги дерева
полностью определяет соответствующее
фундаментальное сечение.
дерева Т, а ориентация сечения S
согласована с ориентацией дуги
.
Следовательно, задание дуги дерева
полностью определяет соответствующее
фундаментальное сечение.
На рисунке пунктирами показаны
фундаментальные сечения
![]() по дереву Т.
по дереву Т.
![]()

Фундаментальной матрицей
![]() ,
по дереву T, называется
матрица, строками которой являются
вектор-сечения, фундаментальные по
дереву Т. Выделенному дереву Т на рисунке
отвечает фундаментальная матрица
сечений, столбцы которой помечены
номерами дуг всего графа, строки –
номерами дуг дерева, точнее, номерами
соответствующих фундаментальных
сечений:
,
по дереву T, называется
матрица, строками которой являются
вектор-сечения, фундаментальные по
дереву Т. Выделенному дереву Т на рисунке
отвечает фундаментальная матрица
сечений, столбцы которой помечены
номерами дуг всего графа, строки –
номерами дуг дерева, точнее, номерами
соответствующих фундаментальных
сечений:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
2 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
= 3 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
4 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
5 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
6 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
Фундаментальным циклом графа D
(по дереву T) называется
всякий цикл, содержащий в точности одну
дугу
кодерева D\T
и ориентированный согласованно с
направлением дуги
.
Ясно, что каждая дуга e
кодерева (кодеревом
![]() называется дополнением
называется дополнением
![]() однозначно задает фундаментальный цикл
однозначно задает фундаментальный цикл
![]() ,
который дуга
,
который дуга
![]() замыкает на дереве Т.
замыкает на дереве Т.
Фундаментальной матрицей циклов
(по дереву Т) называется матрица, строки
которой есть все фундаментальные
вектор-циклы по дереву Т. Если на графе
фундаментальные вектор-циклы поменять
номерами задающих дуг кодерева
![]() ,
то фундаментальная матрица циклов
такова:
,
то фундаментальная матрица циклов
такова:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
7 |
1 |
-1 |
-1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
=8 |
0 |
0 |
-1 |
-1 |
0 |
0 |
0 |
1 |
0 |
0 |
9 |
0 |
0 |
-1 |
-1 |
-1 |
0 |
0 |
0 |
1 |
0 |
10 |
0 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
1 |
Замечание. Относительно разбиения
множества всех дуг
![]() на дуги дерева и кодерева фундаментальные
матрицы сечений и циклов разбиваются
на блоки вда:
на дуги дерева и кодерева фундаментальные
матрицы сечений и циклов разбиваются
на блоки вда:
![]()
![]()
![]() ;
;
![]() ;
;
Информационные блоки
![]() ,
,![]() фундаментальных матриц
фундаментальных матриц
![]() (по одному дереву)
виражаються друг через друга по формуле:
(по одному дереву)
виражаються друг через друга по формуле:
![]() ;
;
![]()
Поэтому достаточно вычислить одну из
фундаментальных матриц
или
![]() .
.
