
- •2) Частный случай
- •Трение.
- •Трение качения в высших кинематических парах.
- •Уравновешивание масс механизмов.
- •Основные сведения о структуре манипуляторов.
- •Метод преобразования координат в матричной.
- •Прямая задача кинематики манипуляторов.
- •Обратная задача кинематики манипулятора.
- •Силовой расчет манипулятора.
- •Основная теорема зацепления.
- •Основные геометрические характеристики зубчатых колес.
- •Основные свойства и характеристики эвольвентного зацепления.
- •Качественные показатели зацепления.
- •1) Угол перекрытия.
- •Особенности внутреннего зацепления.
- •Основные параметры кулачковых механизмов.
Прямая задача кинематики манипуляторов.
Задача состоит в определении положения, скоростей и ускорений его звеньев и отдельных точек по известным законам изменения его обобщенных координат.
![]()
С
каждым звеном связываем систему
координат.
![]() - неподвижная, остальные – подвижные.
- неподвижная, остальные – подвижные.
Обобщенные координаты:
![]() - угол поворота
звена “1” относительно звена “0” вокруг
оси
- угол поворота
звена “1” относительно звена “0” вокруг
оси
![]()
![]() - перемещение звена
“2” относительно звена “1” вдоль оси
- перемещение звена
“2” относительно звена “1” вдоль оси
![]()
![]() - угол поворота
звена “3” относительно звена “2” вокруг
оси
- угол поворота
звена “3” относительно звена “2” вокруг
оси
![]()
В
задаче о положениях определим координаты
центра схвата
![]() в неподвижной системе координат
в неподвижной системе координат
![]() ,
если известны координаты точки
в системе
,
если известны координаты точки
в системе
![]()
![]()
Для этого осуществляем последовательный переход от системы к системе
![]()
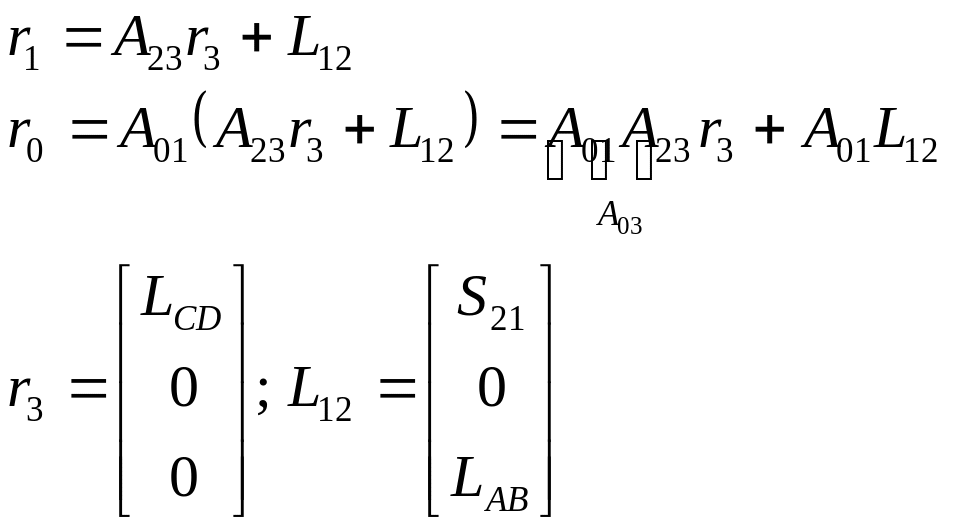

Матрица
![]() полностью определяет ориентацию руки
“3” в неподвижной системе координат
полностью определяет ориентацию руки
“3” в неподвижной системе координат
![]() ,
так как столбцы этой матрицы представляют
собой направление косинуса осей
,
так как столбцы этой матрицы представляют
собой направление косинуса осей




Угловая скорость любого звена манипулятора определяется на основании соотношения:
![]()
![]() - абсолютная
частота.
- абсолютная
частота.
![]() - переносная
частота.
- переносная
частота.
![]() - относительная
частота.
- относительная
частота.

![]() относительно звена
“1”
относительно звена
“1”
![]() ,
так как звенья “2” и “1” связаны
поступательной парой.
,
так как звенья “2” и “1” связаны
поступательной парой.
![]()
Запишем в неподвижной системе координат:

Угловое
ускорение
![]() получим путем дифференцирования
выражения угловой скорости:
получим путем дифференцирования
выражения угловой скорости:

Линейные скорости и ускорения точек можно получить путем дифференцирования выражений координат:
![]()

Обратная задача кинематики манипулятора.
Эта задача состоит в определении таких законов изменения обобщенных координат, которые обеспечивают заданное перемещение схвата.
Положение схвата может быть задано с помощью шести величин, причем три из них – координаты цента схвата, а остальные три – определяют ориентацию схвата в пространстве. В качестве таких параметров можно принять направляющие косинусы одной оси и один – другой оси:
 ,
где “n”
– последнее звено со схватом.
,
где “n”
– последнее звено со схватом.
Тогда
в качестве направляющих косинусов можно
принять
![]() .
В результате получим шесть уравнений
с неизвестными обобщенными координатами.
.
В результате получим шесть уравнений
с неизвестными обобщенными координатами.
Если
![]() ,
то число неизвестных равно числу
уравнений и система имеет решение.
,
то число неизвестных равно числу
уравнений и система имеет решение.
Если
![]() ,
то система имеет множество решений.
,
то система имеет множество решений.
Если
![]() ,
то система не имеет решений.
,
то система не имеет решений.
Если
требуется попадание центра схвата в
определенную точку, а ориентация значения
не имеет, то эта задача решается
манипулятором с
![]() .
.
Рассмотрим
обратную задачу на примере манипулятора
![]()
Известны координаты центра схвата:
![]() .
.
Определить:
![]()
Используем формулы (1), (2) и (3), полученные при решении прямой задачи:
Разделим (2) на (1):

Из выражения (3) находим :
![]()
Из выражения (1) находим :
![]()
Если
задана траектория центра схвата
![]() ,
то расчет по формулам (4) – (6) повторяется
многократно для каждого положения
,
то расчет по формулам (4) – (6) повторяется
многократно для каждого положения
![]() .
.
Силовой расчет манипулятора.
Эта задача состоит в определении реактивных сил и моментов в кинематических парах, а также движущих сил и моментов приводных двигателей. Эта задача решается методом кинетостатики, основанном на принципе Даламбера.
Главный вектор сил инерции звена:
![]()
Главный момент сил инерции определяется в подвижной системе координат, связанной со звеном:
![]()
 - тензор инерции
в центре масс.
- тензор инерции
в центре масс.
Осевые моменты инерции:
![]()
Центральные моменты инерции:

Если координатные оси совпадают с главными центральными осями инерции, то центробежные моменты инерции равны нулю. Такими осями являются оси инерции. В этом случае:

Рассмотрим силовой расчет манипулятора . Находим силы инерции звеньев и транспортируемой детали:


Определяем моменты сил инерции звеньев:

Расчет начинаем с последнего звена “3”. Рисуем его расчетную схему.
Уравнение сил:
![]()
![]() - сила тяжести
детали.
- сила тяжести
детали.
![]() - сила тяжести
звена “3”.
- сила тяжести
звена “3”.
![]() - неизвестная
реакция звена “3” со стороны звена “2”.
- неизвестная
реакция звена “3” со стороны звена “2”.


!!!!!!
Уравнение равновесия моментов относительно точки “C”:
![]()
![]() - неизвестный
реактивный момент, действующий на звено
“3” со стороны звена “2”. Находим
- неизвестный
реактивный момент, действующий на звено
“3” со стороны звена “2”. Находим
![]() :
:


В
результате векторное уравнение моментов
приводится к трем скалярным уравнениям,
из которых определяется
![]() :
:

![]() - движущий момент
во вращательной паре “C”.
- движущий момент
во вращательной паре “C”.
Известными
являются
![]() .
.
Из
уравнения равновесия определяется
![]()
![]() - движущая сила в
поступательной паре “B”.
- движущая сила в
поступательной паре “B”.
Последним рассматривается звено “1”:
![]()
Из
уравнения равновесия определяется
![]()
![]() - движущий момент
во вращательной паре “A”.
- движущий момент
во вращательной паре “A”.
