6. Понятие идеального газа.

Идеальным называется газ, у которого объемы молекул бесконечно малы и отсутствуют силы молекулярного взаимодействия. Молекулы идеального газа представляют собой материальные точки, взаимодействие между которыми ограничено молекулярными соударениями.

Любой реальный газ тем ближе к идеальному, чем ниже его давление и выше температура. Например, окружающий нас воздух можно считать идеальным газом. Понятие идеального газа и законы идеальных газов полезны в качестве предела законов реального газа.

На практике часто приходится иметь дело с газами при невысоких давлениях, поэтому расчеты различных термодинамических процессов с достаточной степенью точности можно проводить по уравнениям идеального газа.

7. Уравнение состояния идеального газа.

Из уравнений , и , следует, что .

Рассмотрим 1 кг газа. Учитывая, что в нем содержится N молекул и, следова­тельно, , получим: .

Постоянную величину Nk, отнесен­ную к 1 кг газа, обозначают буквой R и называют газовой постоян­ной. Поэтому

, или . (1.3)

Полученное соотношение представляет собой уравнение Клапейрона.

Умножив (1.3) на М, получим урав­нение состояния для произвольной массы газа М:

. (1.4)

Уравнению Клапейрона можно при­дать универсальную форму, если отнести газовую постоянную к 1 кмолю газа, т. е. к количеству газа, масса которого в килограммах численно равна молеку­лярной массе μ. Положив в (1.4) М=μ и V=V μ, получим для одного моля урав­нение Клапейрона — Менделеева:

.

Здесь — объем киломоля газа, а — универсальная газовая постоянная.

В соответствии с законом Авогадро (1811г.) объем 1 кмоля, одинаковый в одних и тех же условиях для всех иде­альных газов, при нормальных физических условиях равен 22,4136 м³, поэтому

Газовая постоянная 1 кг газа составляет .

8. Газовые смеси. Закон Дальтона.

В инженерной прак­тике часто приходится иметь дело с газо­образными веществами, близкими по свойствам к идеальным газам и пред­ставляющими собой механическую смесь отдельных компонентов различных газов, химически не реагирующих между собой. Это так называемые газовые сме­си. В качестве примера можно назвать продукты сгорания топлива в двигателях внутреннего сгорания, топках печей и па­ровых котлов, влажный воздух в сушиль­ных установках и т. п.

Основным законом, определяющим поведение газовой смеси, является закон Дальтона: полное давление смеси иде­альных газов равно сумме парциальных давлений всех входящих в нее компо­нентов:

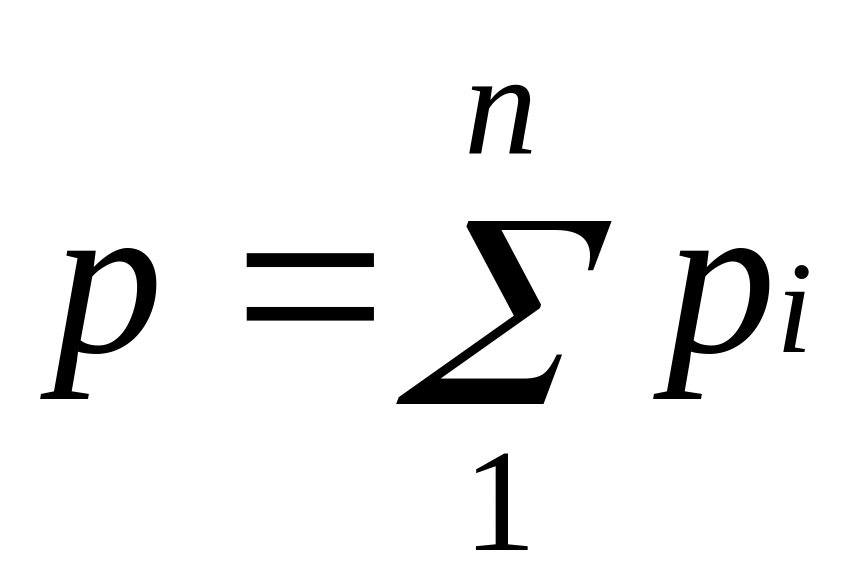
Парциальное давление pi — давление, которое имел бы газ, если бы он один при той же температуре занимал весь объем смеси.

9. Способы задания состава газовых смесей.

Состав га­зовой смеси может быть задан массовы­ми, объемными или мольными долями.

Массовой долей называется отношение массы отдельного компонента Мi, к массе смеси М:

.

Очевидно, что и .

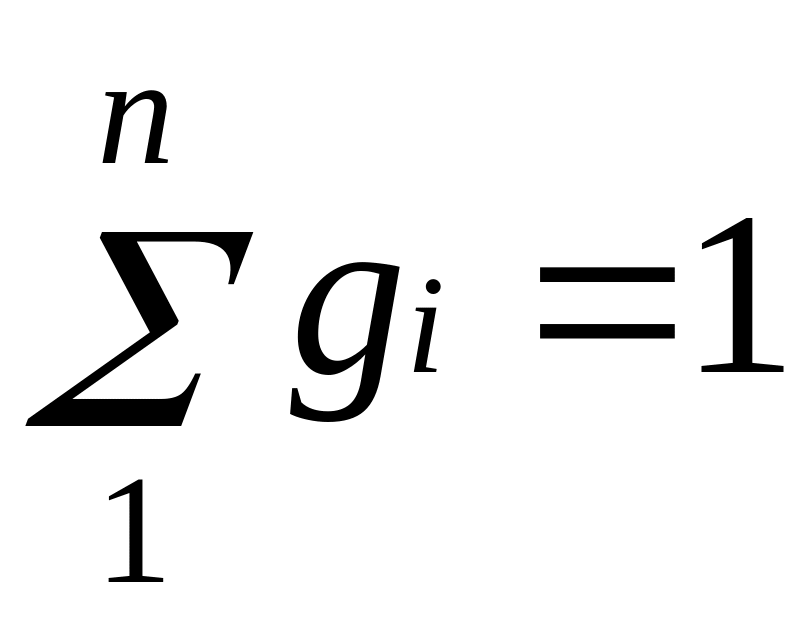Массовые доли часто задаются в процентах. Например, для сухого воздуха ; .

Объемная доля представляет собой отношение приведенного объема газа V, к полному объему смеси V: .

Приведенным называется объем, который занимал бы компонент газа, ес­ли бы его давление и температура равня­лись давлению и температуре смеси.

Для вычисления приведенного объема запишем два уравнения состоя­ния i-го компонента:

; (2.1)

.

Первое уравнение относится к состоянию компонента газа в Смеси, когда он имеет парциальное давление pi и занимает пол­ный объем смеси, а второе уравнение — к приведенному состоянию, когда давле­ние и температура компонента равны, как и для смеси, р и Т. Из уравнений следует, что

. (2.2)

Просуммировав соотношение (2.2) для всех компонентов смеси, получим с учетом закона Дальтона 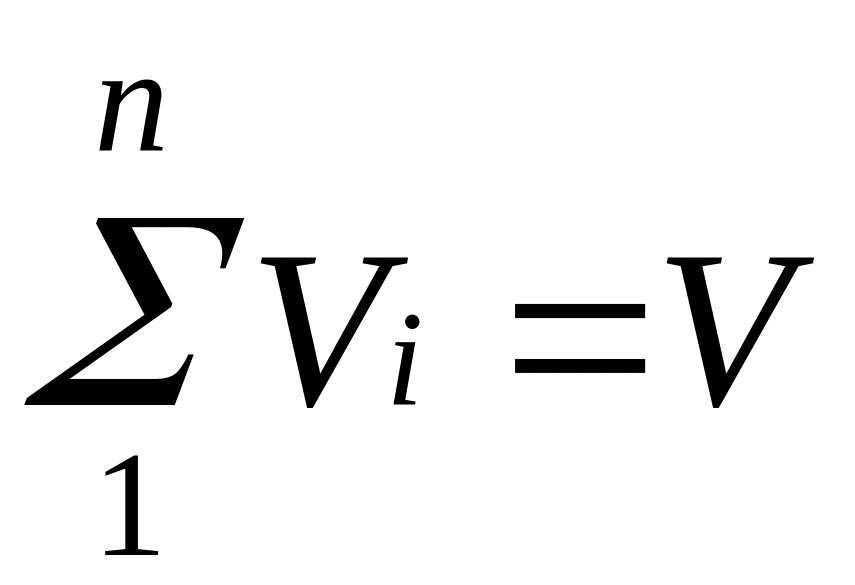,откуда 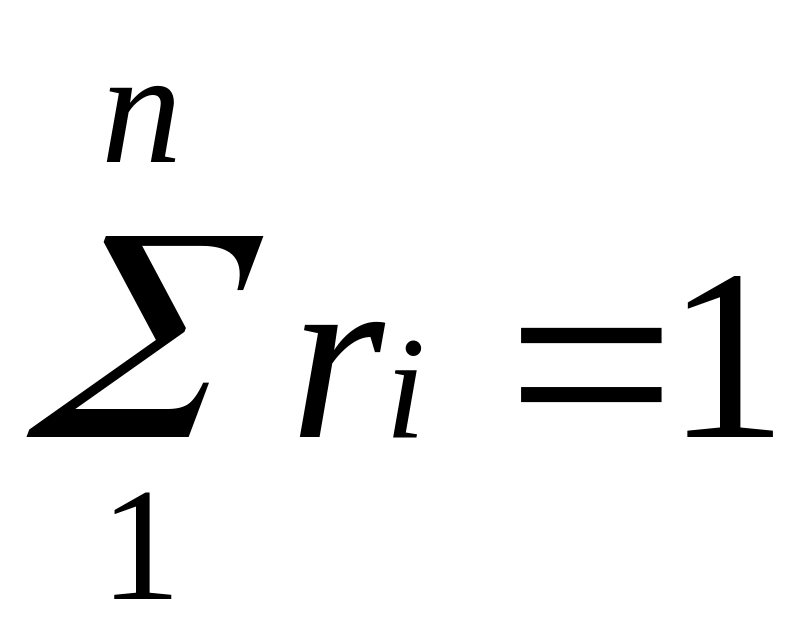. Объемные доли также часто задаются в процентах. Для воз­духа , .

Иногда бывает удобнее задать со­став смеси мольными долями. Моль­ной долей называется отношение количества молей Ni рассматриваемого компонента к общему количеству молей смеси N.

Пусть газовая смесь состоит из N1 молей первого компонента, N2 молей вто­рого компонента и т. д. Число молей смеси 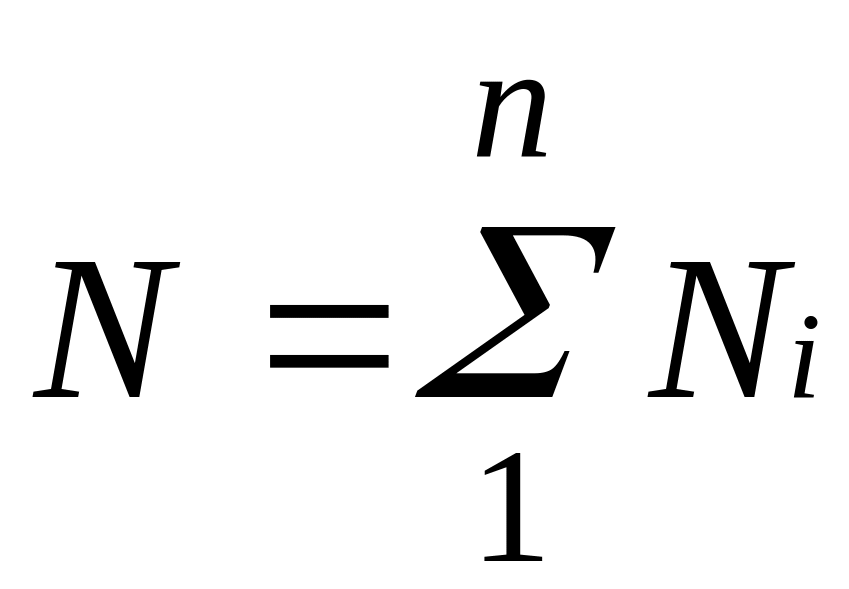, а мольная доля компонента будет равна .

В соответствии с законом Авогадро объемы моля любого газа при одинако­вых р и Т, в частности при температуре и давлении смеси, в идеально газовом состоянии одинаковы. Поэтому приве­денный объем любого компонента может быть вычислен как произведение объема моля на число молей этого компо­нента, т. е. а объем смеси — по формуле . Тогда , и, следовательно, задание смесильных газов мольными долями равно заданию ее объемными долями.