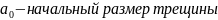- •Модели прочностной надежности.
- •Нормальные и касательные напряжения, правила знаков.
- •Свойство парности касательных напряжений. Виды напряженного состояния.
- •Напряжения на произвольной косой площадке.
- •Главные площадки и главные напряжения. Инварианты напряженного состояния в точке. Тензор напряжений.
- •Дифференциальные уравнения равновесия.
- •Краевые условия для напряжений.
- •Д еформированное состояние в точке, тензор деформаций. Инварианты тензора деформаций. Связь деформаций с перемещениями точек твердого тела (уравнения Коши).
- •Закон Гука для упругой изотропной среды.
- •Постановка задачи теории упругости, прямая и обратная задача.
- •Способы и методы решения задачи теории упругости (уравнения).
- •Условная диаграмма растяжения и сжатия, теорема о разгрузке. Эффект Баушингера. Интенсивность напряжений и деформаций.
- •Простое и сложное нагружение, Основные уравнения теории пластичности. Постановка задачи теории пластичности.
- •Теорема Ильюшина о простом нагружении. Метод переменных параметров.
- •Усталость материалов. Кривые выносливости, уравнения. Влияние факторов на усталостную прочность.
- •Термоусталость. Малоцикловая усталость, виды нагружения, уравнение Коффина, уравнения Менсона.
- •Гипотезы накопления усталостных повреждений. Линейная модель накопления усталостных повреждений.
- •Зарождение, развитие трещин. Напряженное состояние при вершине трещины. Коэффициент интенсивности напряжений.
- •Критерии роста трещины. Уравнение Периса. Прогноз ресурса детали с трещиной.
- •Основы метода конечных элементов, этапы решения, матричная форма записи уравнений теории упругости. Функции формы конечного элемента.
- •Матрица жесткости конечного элемента. Разрешающие уравнения метода конечных элементов.
- •Ползучесть, основы моделей ползучести. Теория старения.
- •Теория течения и теория упрочнения. Установившаяся ползучесть. Длительная прочность.
- •Экспериментальное исследование прочности гтд. Определения. Оценка статической прочности. Оценка динамической прочности.
- •Э квивалентно-циклические испытания. Испытания лопаток, замковых соединений, ободов дисков. Способы измерения деформаций. Стратегии управления ресурсом.
- •Теория колебаний. Связи. Обобщенные координаты. Виртуальные перемещения. Обобщенные силы. Условия равновесия.
- •Уравнение Лагранжа. Свободные колебания системы с одной степенью свободы (начальные условия, уравнения, определения). Свободные колебания системы при сопротивлении.
- •Нормальные координаты и главные колебания.
- •Уравнение частот, собственные формы колебаний и их свойства
Зарождение, развитие трещин. Напряженное состояние при вершине трещины. Коэффициент интенсивности напряжений.
Накопление усталостных повреждений в материале приводит к нарушению сплошности материала и появлению в нем разрыва - усталостной трещины. Развитие усталостной трещины является последним этапом усталостного разрушения.
Исходные трещины в элементах конструкции могут возникнуть в процессе изготовления. Литейные дефекты, дефекты сварки, химико-термическая обработка, механическая обработка, нанесение гальванических покрытий.
Механизм возникновения усталостных трещин:
Накопление повреждений при циклическом нагружении деформации дислокаций кристаллической решетки, концентрация в зоне максимальных напряжений, образование микронесплошности материала, микротрещины.
А) микротрещины объединяются в магистральную усталостную трещину (макротрещину)
Б) одна из микротрещин преобразуется быстрее и превращается в макротрещину
2) исходный дефект - макротрещина
Типы трещин:
Трещина нормального отрыва, 2. Трещина сдвига, 3. Трещина среза.
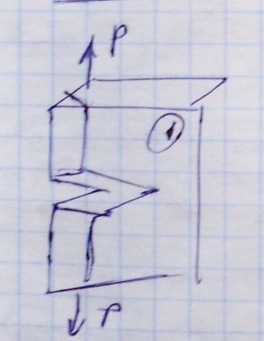
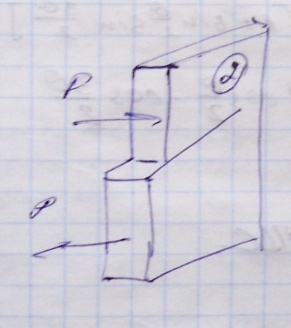
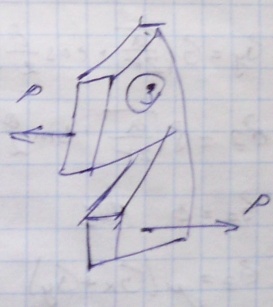
Напряженное состояние при вершине трещины.
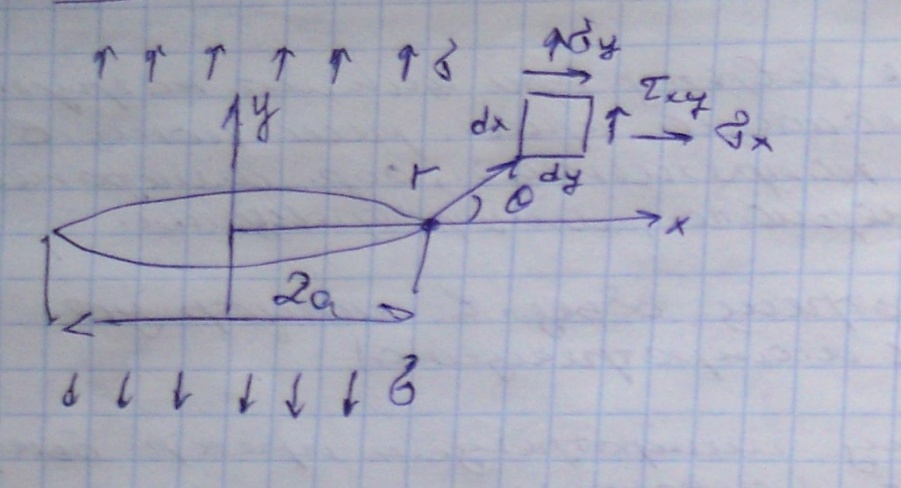
Решение данной задачи представляется в виде рядов:





Коэффициент интенсивности напряжений.
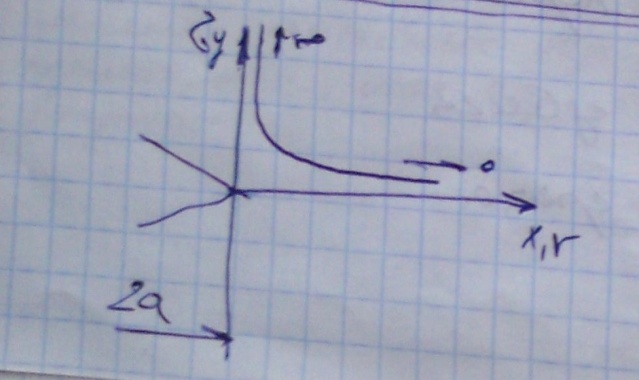
Напряжения
в вершине трещины пропорциональны
внешним напряжениям
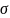 .
Их величина пропорциональна корню
.
Их величина пропорциональна корню
 из размера трещины и стремится к
бесконечности вершины трещины при
из размера трещины и стремится к
бесконечности вершины трещины при
 .
При больших
.
При больших
 ,
,
 .
.
Данная особенность есть следствие а) упругого решения (бесконечность напряжений); б) использование первых членов рядов на большом расстоянии от вершины трещины.
В
уравнениях описывающих напряженное
состояние функции
 имеют простой вид. В обобщенном виде
эти уравнения можно записать:
имеют простой вид. В обобщенном виде
эти уравнения можно записать:
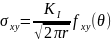
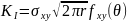
 -
коэффициент интенсивности напряжений.
Функция позволяющая определить и описать
напряженное деформированное состояние
при вершине трещины.
-
коэффициент интенсивности напряжений.
Функция позволяющая определить и описать
напряженное деформированное состояние
при вершине трещины.
Критерии роста трещины. Уравнение Периса. Прогноз ресурса детали с трещиной.
Критерий начала распространения трещин является основой механики разрушения, т.к. не может быть получен из теории упругости или пластичности.
Энергетический критерий (Гриффитса)
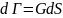
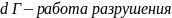

Для
увеличения размера трещины на некоторый
размер
 с увеличением площади поверхности
трещины требуется израсходовать энергию
равную по величине работе, которую надо
затратить, чтобы обеспечить целостность
материала перед трещиной. Эта работа с
обратным знаком есть работа разрушения.
Образование новых участков поверхности
трещины, свободных от нагрузок приведет
к деформированию части тела, что будет
сопровождаться выделением накопленной
в теле упругой энергии.
с увеличением площади поверхности
трещины требуется израсходовать энергию
равную по величине работе, которую надо
затратить, чтобы обеспечить целостность
материала перед трещиной. Эта работа с
обратным знаком есть работа разрушения.
Образование новых участков поверхности
трещины, свободных от нагрузок приведет
к деформированию части тела, что будет
сопровождаться выделением накопленной
в теле упругой энергии.
Было установлено, что работа разрушения, есть работа пластической деформации материала в вершине трещины.
Силовой критерий Ирвина


Предполагая, что зона пластических деформаций в вершине трещины мала по сравнению с размером трещины, высвобождение упругой энергии определяется только деформациями тела, а затраты энергии на разрушение идут на пластические деформации материала.
В случае если граница тела при увеличении трещины остается неподвижна, то работа внешних сил=0 и непосредственно получится выражение:
Если на границах тела действуют постоянные силы, то правая часть уравнения
есть
разница между работой внешних сил и
энергией деформации. Эта разность равна
G.
Для определения потока энергии в вершине
трещины мысленно введем разрез на
поверхностях которого действуют силы,
противоположные силам пытающимся
раскрыть трещину. При раскрытии разреза
на 1 единицу площади работа сил
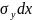 на перемещение
на перемещение
 дает поток энергии:
дает поток энергии:
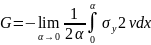
Подставляя
в данное выражение асимптотические
зависимости для
 в вершине трещины получим что:
в вершине трещины получим что:
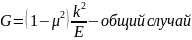
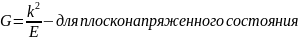
Трещина распространяется при условии если:
Интенсивность высвобождения энергии G достигает критической величины:
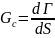
Коэффициент интенсивности напряжения достинает критической величины

Уравнение Периса.
Кинетическая диаграмма усталостных трещин
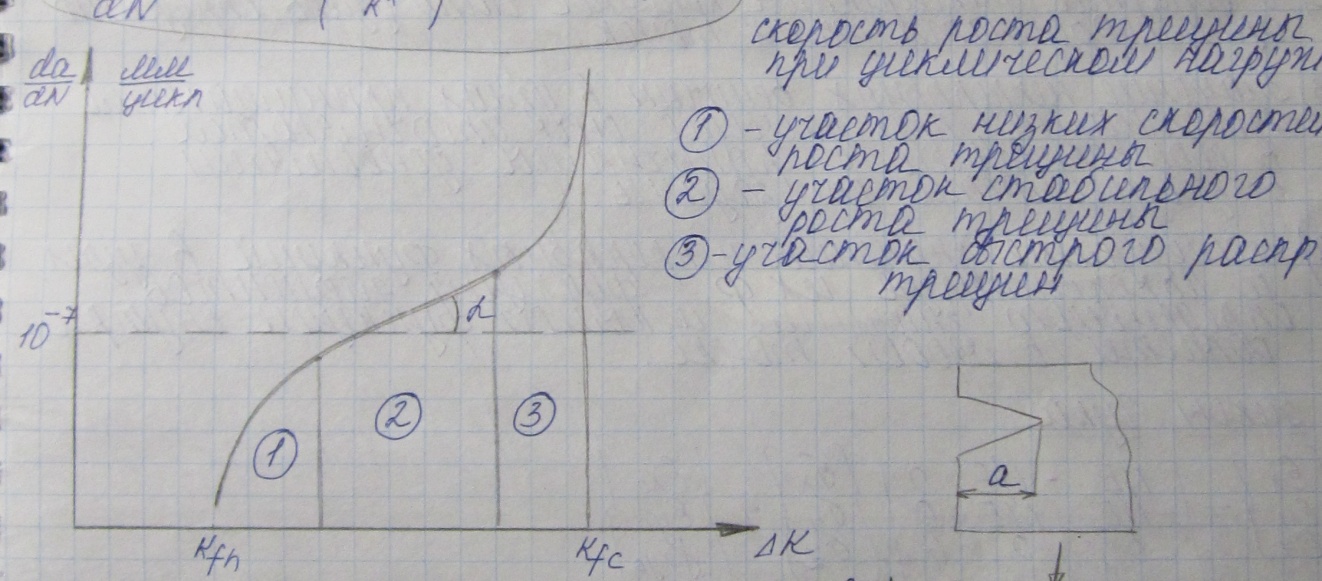

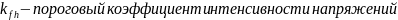
 трещины
не развиваются
трещины
не развиваются

 трещины
распространяются со скоростью звука
трещины
распространяются со скоростью звука
2 участок Перис предложил описать степенным уравнением:

Прогноз ресурса детали с трещиной.
Исходными
данными для анализа являются действующие
напряжения, характеристики трещиностойкости
материала
 ,
,
 ,
,
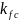 ,
n
и начальный размер трещин.
,
n
и начальный размер трещин.
По
действующим напряжениям определяют
 :
если при всех условиях нагружения
:
если при всех условиях нагружения
 - тещина не развивается; если
- тещина не развивается; если
 - деталь эксплуатироваться не может;
если
- деталь эксплуатироваться не может;
если
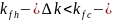 трещина развивается, необходимо
определить ресурс детали до поломки.
Для этого используют уравнение Периса:
трещина развивается, необходимо
определить ресурс детали до поломки.
Для этого используют уравнение Периса: