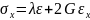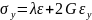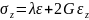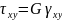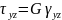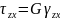7. Краевые условия для напряжений.

Равновесие элементов, примыкающих к поверхности тела, обеспечивается силами, действующими на поверхности. И наоборот, силы на поверхности уравновешиваются напряжениями, возникающими в теле.

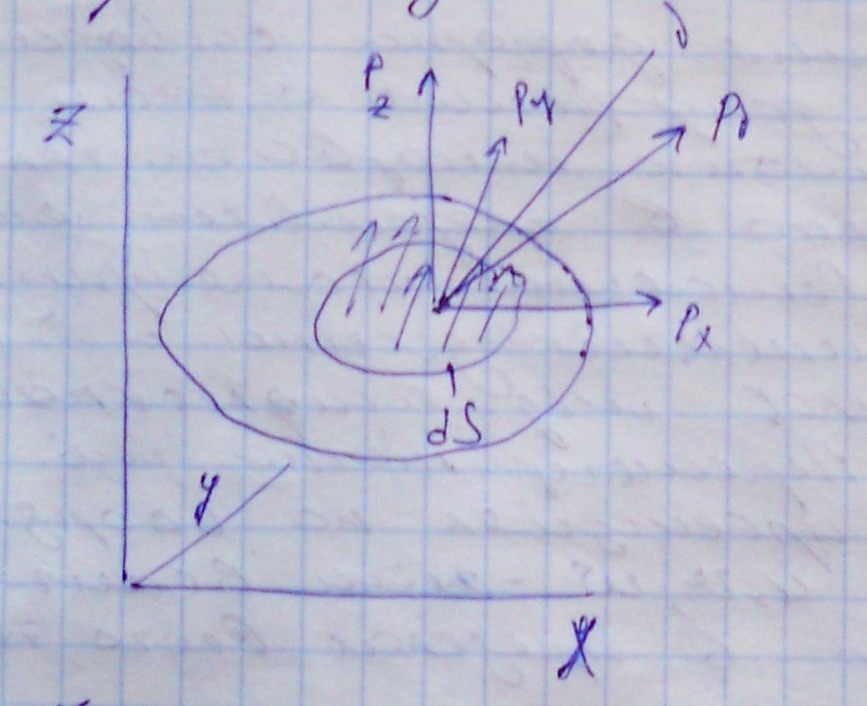
Нагрузку на поверхности тела можно представить как вектор напряжений , действующий на поверхности dS. Элемент поверхности dS, ввиду его малости, можно рассматривать как площадку с нормалью V, напряжение, возникшее в теле можно связать с нагрузками на поверхности, используя уравнение системы

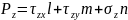
Получим краевые условия:

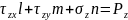
8. Д еформированное состояние в точке, тензор деформаций. Инварианты тензора деформаций. Связь деформаций с перемещениями точек твердого тела (уравнения Коши).

Определение понятия деформации выводится на основании допущения о том, что перемещение точек неподвижного тела возможно только вследствие его деформации. Решается геометрическая задача об изменении длины и взаимных углов между элементами тела. Перемещение точки твердого тела после деформации в проекциях на координатные оси обозначают - эти величины малы и непрерывны в пределах всего тела. Рассмотрим элементарный объем:

Если тело подвергается деформации и 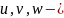компоненты перемещения в точке Р, то перемещение в напряжении оси Х точки А на длине dx составит следующее:

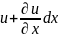
Соответственно увеличение длины ребра РА вследствие деформации равно 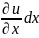. Относительное удлинение в точке Р в направлении оси Х соответственно 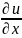. Аналогичное рассуждение справедливо для других осей .

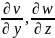Относительное удлинение обозначают 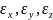- и называют линейной деформацией 1 рода:

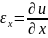
Кроме линейных деформаций твердое тело можно деформировать без изменения объема, сдвигом:

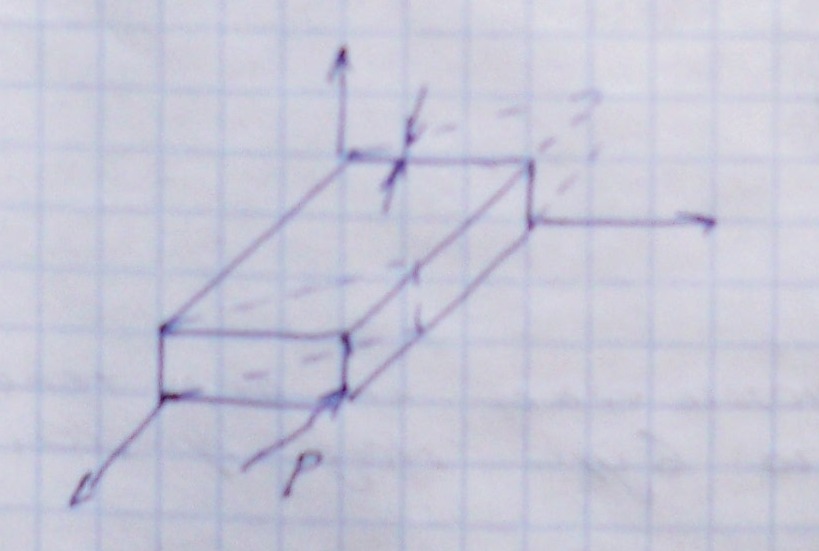
Рассмотрим изменение угла между элементами РА и РВ в плоскости XY

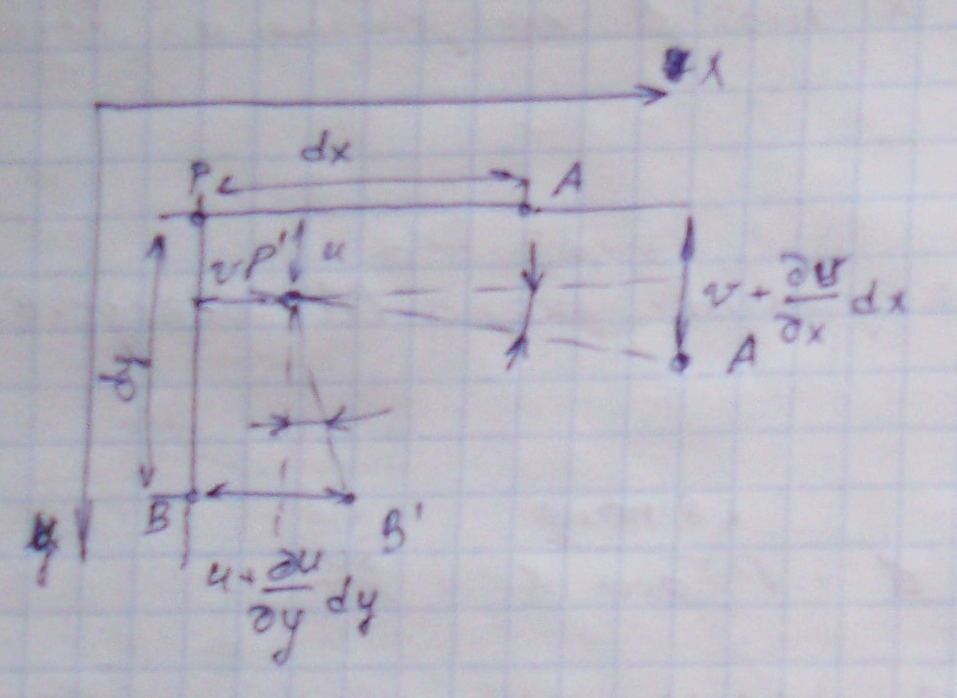
После перемещения, линейный элемент РА переместиться в новое положение P’A’и образует с начальным положением угол 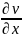. Аналогично P’В’ образует угол . Первоначальный угол между элементами РВ и РА равный 90 уменьшиться на величину 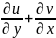- эта величина представляет собой деформацию сдвига между плоскостями и обозначается

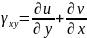
Связь перемещения точек тела и деформаций тела выражается с помощью 6 уравнений, называемых формулами Коши:

6 величин, описывающих деформацию тела, образуют тензор деформаций:

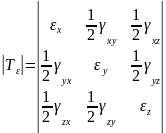
Тензор симметричен относительно главной диагонали, вследствие парности угловых деформаций

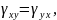
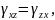
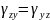
Деформации инвариантны к преобразованию системы координат:

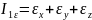
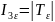
Компоненты тензора деформации не могут быть произвольными величинами, не связанными с - величинами перемещений. Для определения перемещений по величинам деформации они должны удовлетворять 6 уравнениям неразрывности (сплошности):

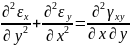
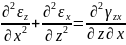
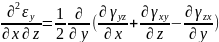
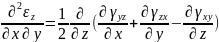
Если уравнения неразрывности деформации не удовлетворяются, то деформация тела происходит с разделением на фрагменты или с образованием надрывов на поверхности.

9. Закон Гука для упругой изотропной среды.

Опытным путем установлено, что процесс деформации конструкционных материалов разделяется на несколько этапов:

1. Характеризуется линейной зависимостью между напряжениями и деформациями.

Р. Гук в 1679 году первым опубликовал о линейной связи деформаций и напряжений. Линейное соотношение между тензором напряжений и тензором деформаций принято называть законом Гука.

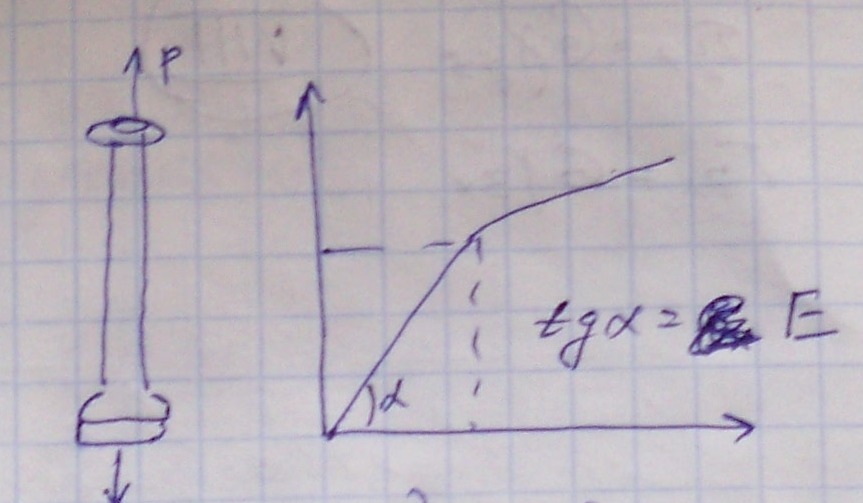
Для трехмерного напряженного состояния закон Гука приобретает другую форму:

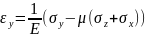
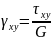
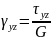
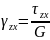
Где - модуль сдвига второго рода

Если решить данную систему относительно напряжений, то получим: