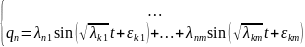26. Уравнение Лагранжа. Свободные колебания системы с одной степенью свободы (начальные условия, уравнения, определения). Свободные колебания системы при сопротивлении.

Для исследования колебательных систем с конечным числом степеней свободы используются уравнения Лагранжа в обобщенных координатах, составленные в предположении о том, что связи, наложенные на систему, идеальны; уравнения не содержат реакций связей; входящие в уравнения величины, определяющие движения системы, непосредственно связаны обобщенными силами.

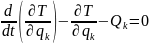
Для консервативных систем уравнение Лагранжа записывается через потенциальную энергию:

В этом случае энергия характеризует полную механическую энергию системы.

Колебания системы с одной степенью свободы.

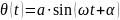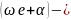Система с одной СС – система, положение которой в пространстве однозначно определяется заданием одной обобщенной координаты. Например математический маятник движется по закону , где начальная фаза, фаза колебаний, 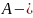амплитуда.

Уравнения малых свободных колебаний системы с одной СС.

Колебания называются свободными, если скорость изменения состояния системы определяется только состоянием самой системы. Такая система – линейный осциллятор.

Система консервативна, уравнение Лагранжа:

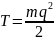
Сопротивление среды равно нулю, поэтому

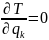
Потенциальная энергия оценивается через жесткость 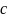системы: /

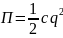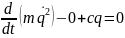
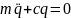
Общее решение: .

Подстановка для решения: , ,

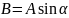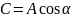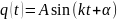
Начальные условия для решения:

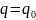
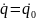
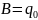
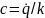
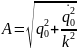
Свободные колебания при наличии сопротивления.

В этом случае на систему действует сила :

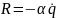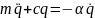
Введем отношение 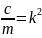, тогда

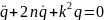
26. Колебания системы с конечным числом степеней свободы, приведенная система. Кинетическая и потенциальная энергия малых свободных колебаний. Уравнение малых колебаний системы около положения устойчивого равновесия.

Детали или механизмы системы на практике являются сложной упругой системой с бесконечным числом степеней свободы. Для определения положения точек при колебаниях в любой момент времени необходимо найти функцию времени и координат точек. При расчетах упругая система заменяется более простой системой с конечным числом степеней свободы – приведенная система.

Кинематическая энергия системы с степеней свободы:

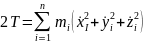
Если выполняется переход к обобщенным координатам:

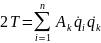
инерционные коэффициенты.

Для колебаний возле положения устойчивого равновесия разложение коэффициентов в ряд по степеням 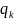ограничивается рассмотрением постоянного коэффициента 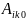, остальные же не рассматриваются ввиду их малости.

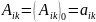
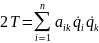
Потенциальная энергия системы может быть выражена через упругие коэффициенты:

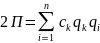
Уравнения малых колебаний системы около положения устойчивого равновесия.

Подставляя в уравнение Лагранжа выражения для кинетической и потенциальной энергий b принимая, что: , можно получить систему дифференциальных уравнений, описывающих колебания системы:

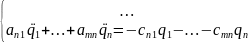
Общее решение данной системы уравнений определяет колебания механической системы.

26. Нормальные координаты и главные колебания.

С помощью линейных преобразований следующего вида:

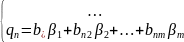
уравнения КЭ и ПЭ преобразуются:

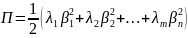
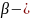нормальные координаты системы. В таких координатах уравнение малых колебаний имеет форму:

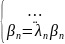
Решение имеет вид:

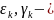из начальных условий.

Ввиду того, что изменение нормальных координат происходит независимо друг от друга, подбирая НУ можно сделать все 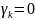, кроме одного.

Во время движения системы:

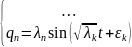
Обобщенные координаты будут изменятся по одному гармоническому закону с одной частотой . Система при этом совершает главные (собственные) колебания. Система с степеней свободы может совершать колебаний со своими главными частотами .

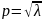В реальных условиях система совершает сложные колебания, которые представляют собой наложение собственных гармонических колебаний.