Расстояние между двумя скрещивающимися прямыми

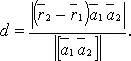
17 Постоянное число а называется пределом последовательности {x_n}, если для любого сколь угодно малого положительного числа eсуществует номер N, что все значения x_n, у которых n>N, удовлетворяют неравенству

                                                                               |x_n - a| < e.                                                                              (6.1)

Записывают это следующим образом:   или x_n→ a.

18 Преде́л фу́нкции (предельное значение функции) в заданной точке, предельнойдля области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке. Определение

Функция   имеет предел   в точке  , предельной для области определения функции  , если для каждой окрестности предела   существует проколотая окрестность точки  , образ которой при отображении   является подмножеством заданной окрестности точки  . Односторо́нний преде́л в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственнолевосторо́нним преде́лом (или преде́лом сле́ва) и правосторо́нним преде́лом (или преде́лом спра́ва). Правосторонний предел принято обозначать любым из нижеследующих способов:

Аналогичным образом для левосторонних пределов приняты обозначения:

19 Первый замечательный предел:

20

Второй замечательный предел:

21 Функция f (x), определенная в некоторой окрестности точки a, называется непрерывной в этой точке, если 

Пусть функция определена в некоторой окрестности точки a, быть может, за исключением самой точки a. Точка a называетсяточкой разрыва, если эта функция либо не определена в точке a, либо определена, но не является непрерывной в точке a.

Чаще всего разрыв возникает по двум причинам:

1. функция задана различными выражениями на разных участках, и в граничных точках эти выражения имеют различные пределы;

2. функция не определена в данной точке.

22 Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как пределотношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке

правило дифференцирования сложной функции) позволяет вычислить производную композиции двух и более функций на основе индивидуальных производных. Если функция f имеет производную в точке x₀, а функция g имеет производную в точке y₀ = f(x₀), то сложная функция h(x) = g(f(x)) также имеет производную в точке x₀.

Если y = f(x) - дифференцируемая функция, заданная уравнением F(x, y) = 0, т. е. F(x, f(x)) ≡ 0 на некотором интервале ]a, b[, то во многих случаях ее производную можно найти из уравнения

23 Пусть для функции z = (х, у) переменные х и у являются функциями переменной t х = x(t), у = y(t). Тогда функция z = (x(t), y(t)) является сложной функцией переменной t

 функция у независимой переменной x называется неявной, если она задана уравнением, не разрешенным относительно y : 

Если функция f задана параметрически x = φ(t), y = ψ(t), α < t < β, где y = f(x) и функции φ и ψ дифференцируемы, причем φ'(t) ≠ 0, то

24 Если f '(x) — производная функции f (x), то производная от нее по независимой переменной x, (f '(x))' = f ''(x), называется производной второго порядка. Аналогично определены производные 3-го, 4-го, , и т.д, n-го порядка: f''' (x) = ( f'' (x))' , f (4)(x) = (f''' (x))' , f ⁽ⁿ⁾(x) = (f ^{(n -1)}(x))' .

Дифференциа́л  — линейная часть приращения функции.

25 Теорема Ролля: если f(a) = f(b) = 0, то имеется точка   максимума или минимума, в которой f' обращается в нуль. Теорема Лагранжа: существует такая точка  , что

Теорема Коши: если   на (a,b), то существует такая точка  , что

Правило Лопита́ля — метод нахождения пределов функций, раскрывающий неопределённости вида 0 / 0 и  . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.

26 Функция f возрастает на множестве P, если для любых x₁ и x₂ из множества P, таких, что x₂>x₁, выполнено неравенство f(x₂) > f(x₁).  Функция f убывает на множестве P, если для любых x₁ и x₂ из множества P, таких, что x₂>x₁, выполнено неравенство f(x₂) < f(x₁).  функция f называется возрастающей на множестве P, если большему значению аргумента из этого множества соответствует большее значение функции. Функция f называется убывающей на множестве P, если большему значению аргумента соответствует меньшее значение функции.

Экстре́мум — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума

27 Пусть функция y=f(x) определена и непрерывна на отрезке [a,b]. Тогда свои наибольшее и наименьшее значения функция достигает в критических точках, лежащих внутки отрезка [a,b], либо на концах отрезка.

Т.о., для нахождения наибольшего и наименьшего значения функции на отрезке нужно:

- найти все критические точки фунции, лежащие внутри отрезка [a,b]

- Вычислить значения функции в этих точках и в точка a и b

- Выбрать наибольшее и наименьшее значения.

28 График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.

График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале.

Точкой перегиба графика функции называется точка, в которой меняется направление выпуклости графика. Для нахождения точ.п. используется теорема (достаточное условие существования т.п.) Если вторая производная f”(x) при переходе ч/з точку x₀, в кот-й она равна нулю или не существует, меняет знак, то точка графика с абсчиссой x₀ есть точка перегиба.

29 Асимптотой графика функции у = f(x) называется прямая, расстояние от которой до текущей точки графика функции стремится к нулю при неограниченном удалении этой точки от начала координат. Бывают вертикальные, горизонтальные, наклонные асимптоты

30 1. Область определения функции

2. Точки пересечения с осями координат. С осью Oy y=f(0).  С осью Ох f(x)=0.Область непрерывности функции и точки разрыва. 3. четность и нечетность .

4.Нахождение производной. 5. Нахождение производной асимптот 6. Нахождение интервала монотонности графика функции.

7. Исследование на точки экстремума

8. Исследование на наличие невертикальных асимптот