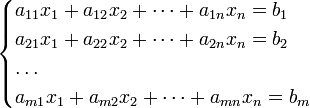1 Матрицы-прямоугольная таблицы чисел, содержащая m строк одинаковой длины(или n столбцов одинаковой длины). Записывается в виде А=а11 а12…(квадратная матрица?). Св-ва обратной матрицы. , где   обозначает определитель.

 для любых двух обратимых матриц A и B.

 где * ^T обозначает транспонированную матрицу.

 для любого коэффициента   .

Если необходимо решить систему линейных уравнений Ax = b, (b — ненулевой вектор) где x — искомый вектор, и если A ^{− 1}существует, то x = A ^{− 1}b. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.

2. Определитель матрицы А обозначается как: det(A), |А| или Δ(A).

Свойства определителей

1. При транспонировании (замене строк определителя на соответствующие столбцы) определитель не изменится.

2. Разложение определителя по любой строке или любому столбцу: определитель равен сумме произведения элементов любого ряда на их алгебраические дополнения.

3. При перестановке двух строк или столбцов абсолютная величина определителя не изменится, а знак определителя меняется на обратный.

4. Общий множитель строки или столбца можно вынести за знак определителя.

5. Свойство линейного преобразования в определителе . Определитель не изменится, если к какой- либо строке (столбцу) прибавить другую строку (столбец) предварительно умноженную на какое- либо число.

6. Если элементы одной строки равны элементам другой строки определителя, то определитель равен нулю .

3 Система m линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида

Для решения СЛАУ матричным способом, нужно найти обратную матрицу. Алгоритм решения (детерминант А=, А^-1=?, А₁₁, А₁₂ и тд., A^*=(……)

4 см.3 Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (только квадратные матрицы).

x 1	+ 2x 2	+ 3x 3	=   4
5x 1	+ 6x 2	+ 7x 3	=   8
4x 1	+ 3x 2	+ 6x 3	=   8

x₁ = Δ₁/Δ решение. Найдем Δ, Δ_x,Δ_y, Δ_z, путем подстановки 4 8 8 в разные с
x₂ = Δ₂/Δ столбцы.
x₃ = Δ₃/Δ

Ме́тод Га́усса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Метод последовательного исключения неихвестных. 2 этапа решения: 1)с-ма приводиться к ступенчатому виду! 2)идет последовательное определение неизвестных из этой ступенчатой с-мы.

Запишем её в виде матрицы 3×4, где последний столбец является свободным членом:

Проведем след.действие п оступенчато приводим к нулю

7  Векторным произведением вектора а на вектор b называется вектор с, который:

1. Перпендикулярен векторам a и b, т. е. са и сb;

2. Имеет длину, численно равную площади параллелограмма, построенного на векторах а и b как на сторонах (см. рис. 17), т. е. 

3.Векторы a, b и с образуют правую тройку.

Геометрический смысл векторного произведения: модуль векторного произведения векторов численно равен площади параллелограмма, построенного на этих векторах как на сторонах

6 Проекция вектора на ось это отрезок заключенный между перпендикулярами проведёнными от концов вектора к оси. свойства проекций. 1.Проеция вектора   на ось L равна произведению модуля вектора   на косинус угла между вектором и осью: 2Проекция суммы двух векторов на ось равна сумме проекций векторов на ту же ось:  .3Если вектор   умножается на число λ, то его проекция на ось также умножается на это число: .

a=a_xi+a_yj+a_zk   Эта формула является основной в векторном исчислении и называется разложением вектора по ортам координатных осей. Числа а_х, а_у, a_z называются координатами вектора а, т. е. координаты вектора есть его проекции на соответствующие координатные оси. Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.

5 Вектор-направленный прямолинейный отрезок,т.е.отрезок имеющий определенныю длину и направление. Бывают: коллинеарными(если они лежат на одной или на параллельных прямых), равными(если они коллинеарны, одинаково направлены и имеют одинаковые длины), компланарными(если они лежат в одной плоскости или в параллельных плоскостях)

Линейными операциями называют операции сложения и вычитания векторов и умножения вектора на число.