Вариант 9.

1. Проверить, является ли система векторов линейно зависимой:

f₁=(5;-1;-3;0), f₂=(1;0;0;3), f₃=(4;-1;-3;-6).

Найти длину каждого вектора, определить координаты вектора .

2. Найти ранг матрицы .

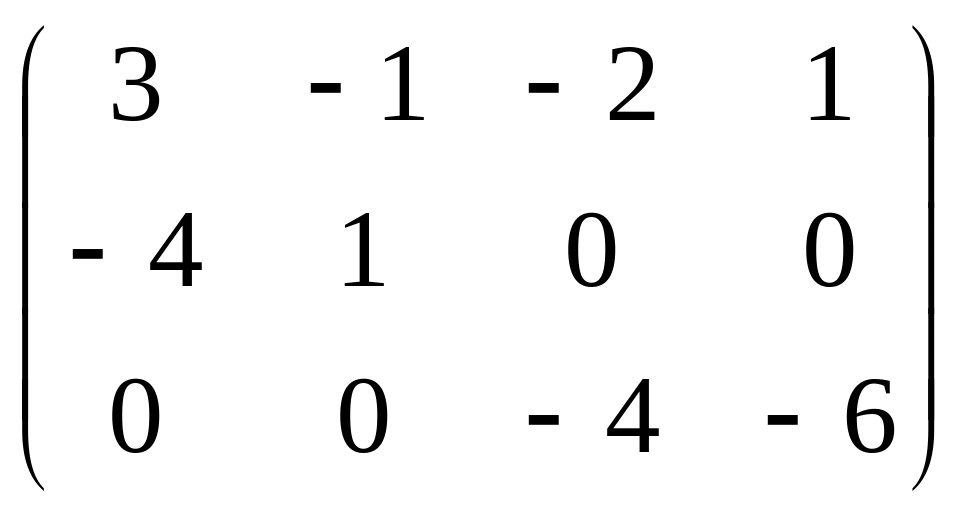3. Решить систему уравнений методом Гаусса

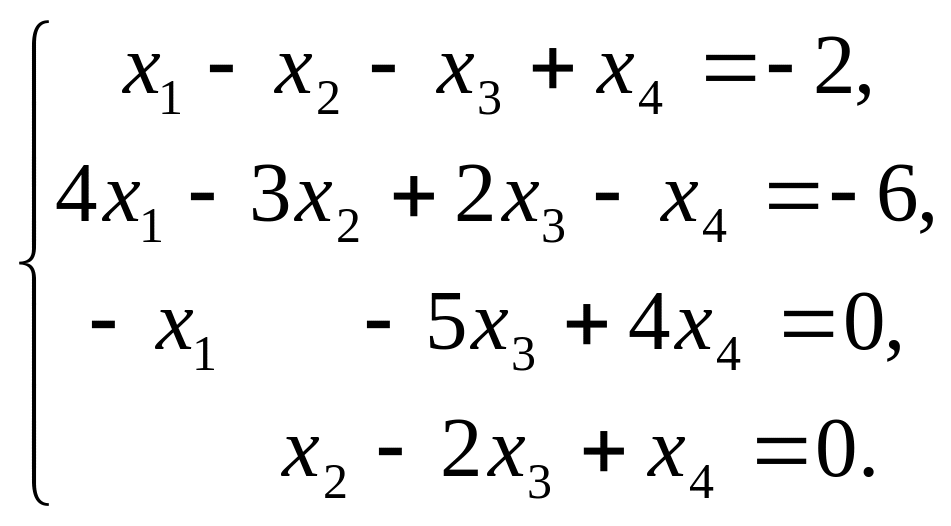
4. Вычислить определитель матрицы .

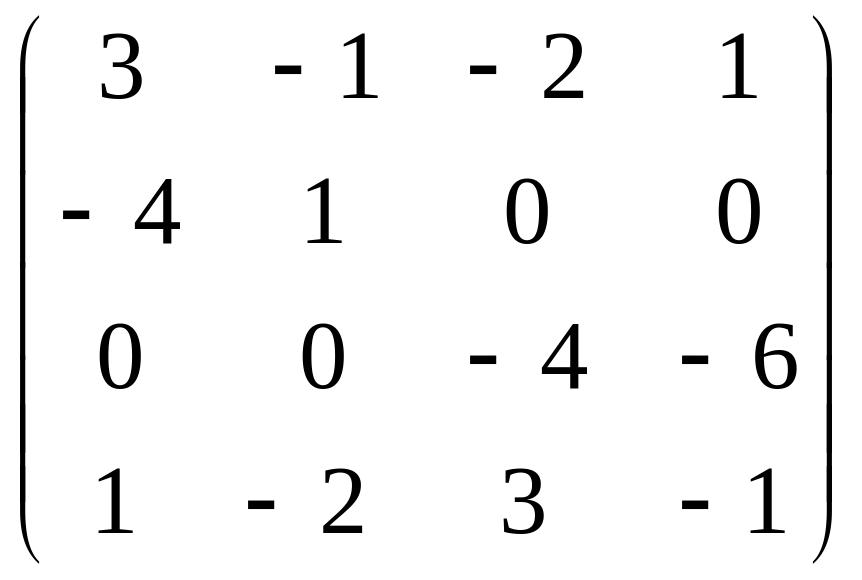5. Привести матрицу к каноническому виду .

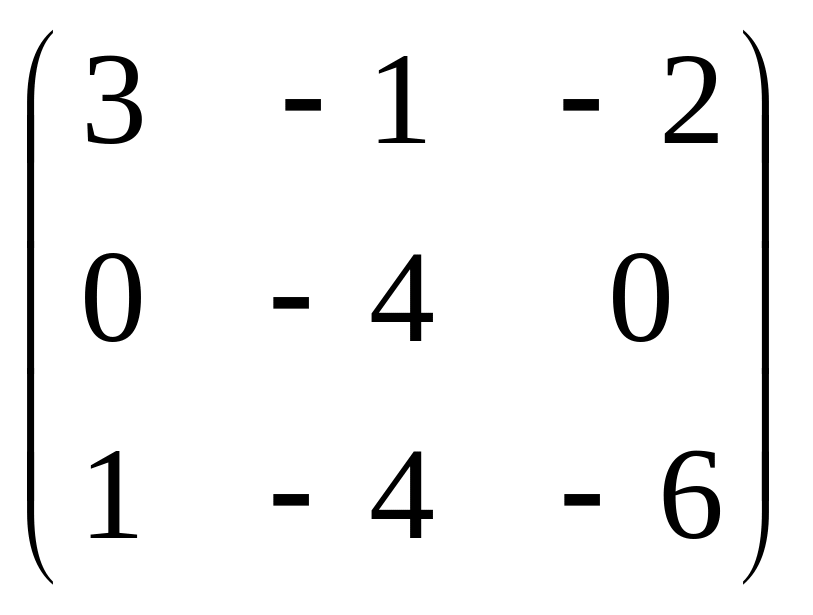6. Написать уравнение прямой, проходящей через заданные точки А(0;-3), В(-3;0). Построить эту прямую и привести уравнение к виду в отрезках на осях.

Написать уравнение пучка прямых, проходящих через А, и выбрать из пучка прямую перпендикулярную АВ.

7. Написать уравнение линии, проходящей через точки А(0;0), В(1;-3) и симметричная относительно оси Ох. Построить ее.

8. Преобразовать к каноническому виду уравнение и построить кривую.

9. Написать уравнение плоскости, проходящей через точку А(4;0;3) и ось Оу. Построить ее.

10. Построить поверхность .

Вариант 10.

1. Проверить, является ли система векторов линейно зависимой:

f₁=(4;-4;-2;4), f₂=(-1;0;0;3), f₃=(1;-2;-1;1).

Найти длину каждого вектора, определить координаты вектора .

2. Найти ранг матрицы .

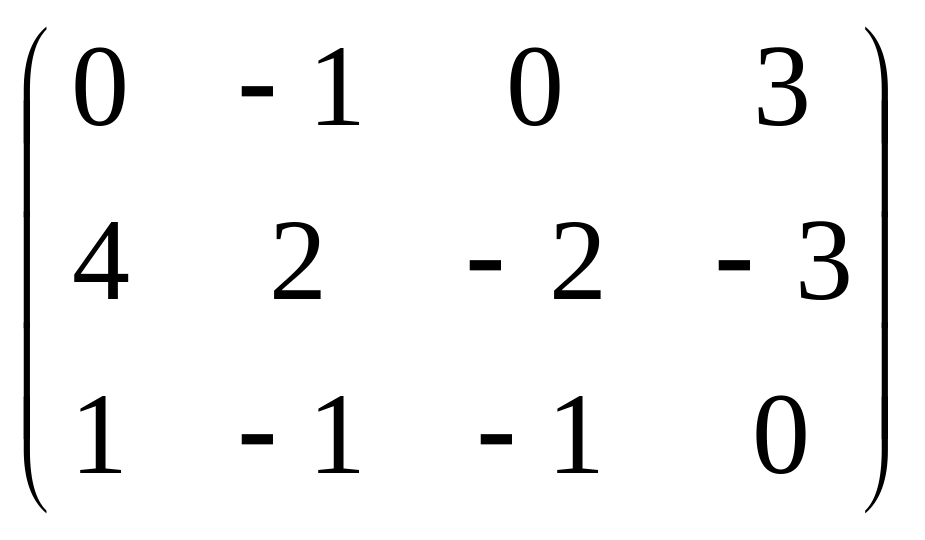3. Решить систему уравнений методом Гаусса

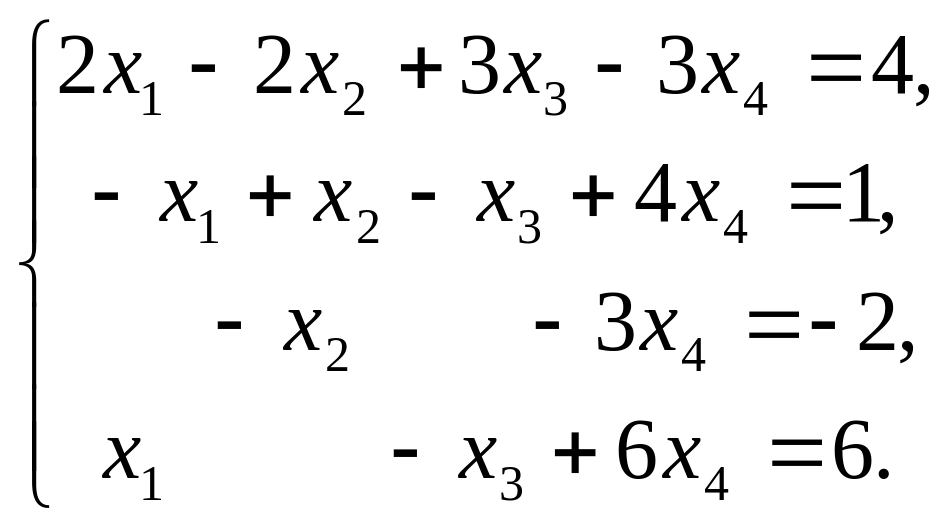
4. Вычислить определитель матрицы .

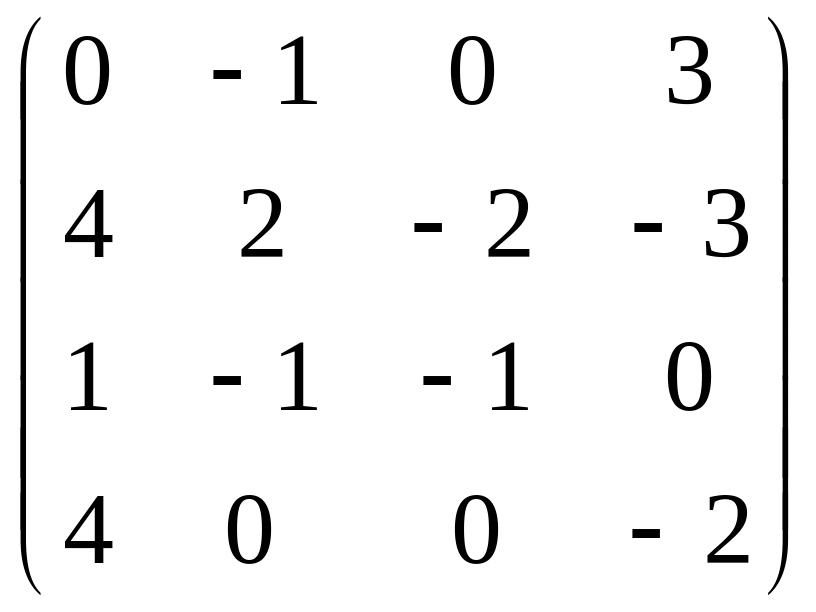5. Привести матрицу к каноническому виду .

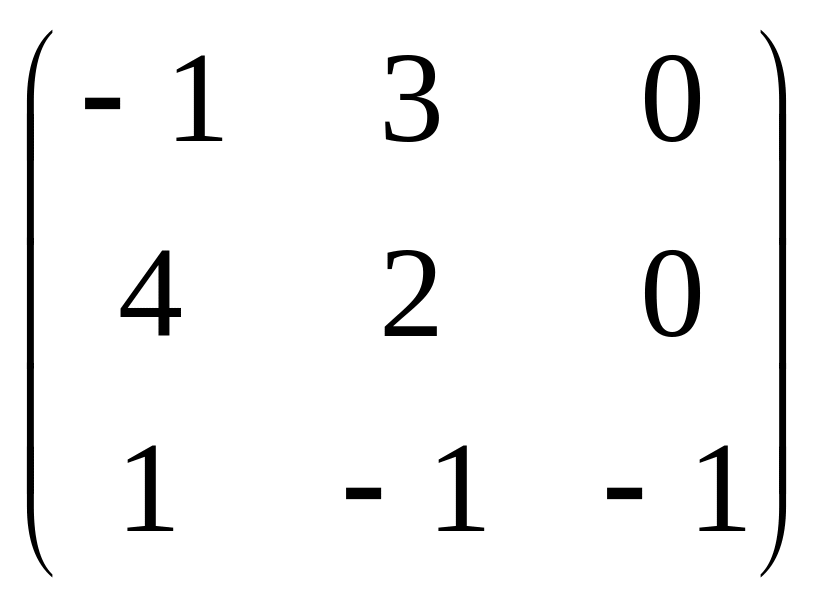6. Написать уравнение прямой, проходящей через заданные точки А(0;1), В(-1;0). Построить эту прямую и привести уравнение к виду в отрезках на осях.

Написать уравнение пучка прямых, проходящих через А, и выбрать из пучка прямую перпендикулярную АВ.

7. Написать уравнение линии, проходящей через точки А(0;0), В(2;-4) и симметричная относительно оси Оу. Построить ее.

8. Преобразовать к каноническому виду уравнение и построить кривую.

9. Написать уравнение плоскости, проходящей через точки А(2;2;0) и В(4;0;0) и параллельной оси Оz. Построить ее.

10. Построить поверхность .

Вариант 11.

1. Проверить, является ли система векторов линейно зависимой:

f₁=(0;-2;-8;0), f₂=(1;0;-1;2), f₃=(-1;-1;-5;-2).

Найти длину каждого вектора, определить координаты вектора .

2. Найти ранг матрицы .

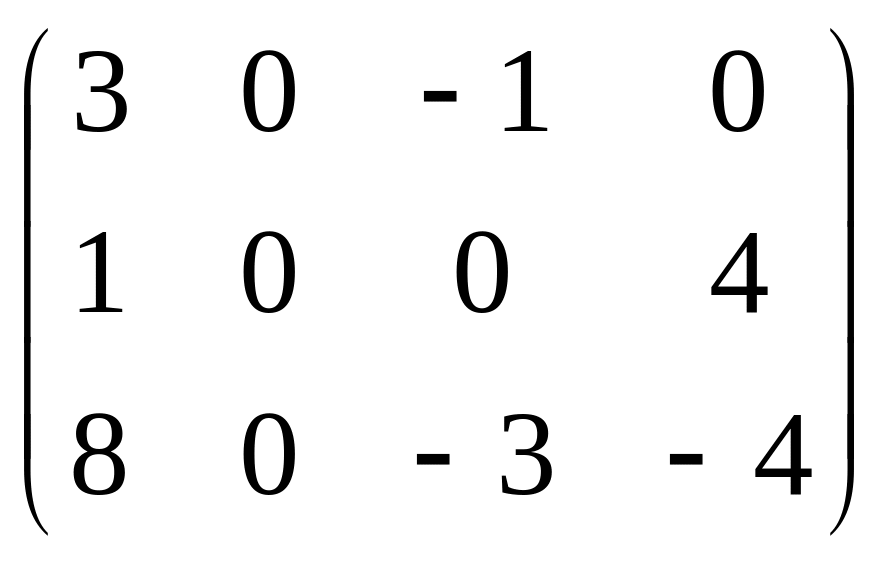3. Решить систему уравнений методом Гаусса

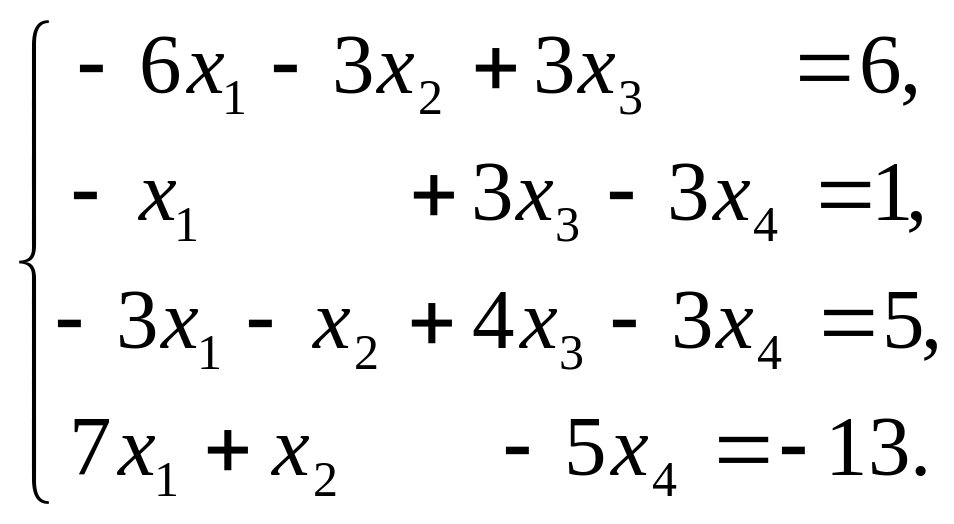
4. Вычислить определитель матрицы .

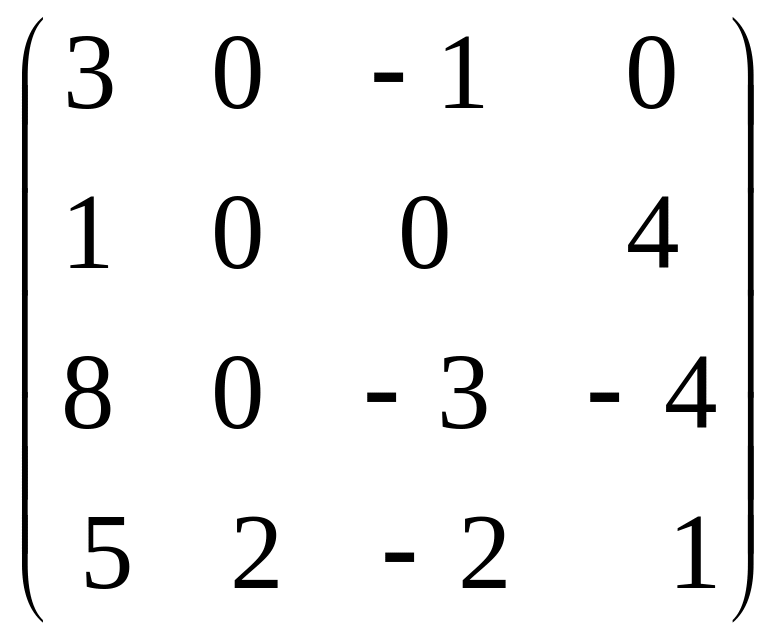5. Привести матрицу к каноническому виду .

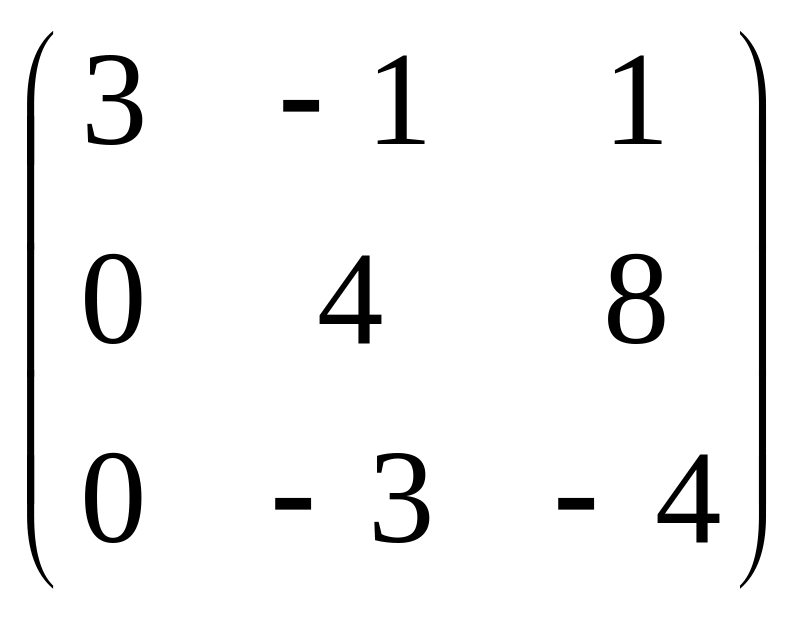6. Написать уравнение прямой, проходящей через заданные точки А(-7;1), В(-1;5). Построить эту прямую и привести уравнение к виду в отрезках на осях.

Написать уравнение пучка прямых, проходящих через А, и выбрать из пучка прямую перпендикулярную АВ.

7. Написать уравнение линии, которая при движении точки М остается равноудаленной от начала координат и от прямой . Построить ее.

8. Преобразовать к каноническому виду уравнение и построить кривую.

9. Написать уравнение плоскости, проходящей через точки А(1;-1;2), В(2;1;2) и С(1;1;4). Построить ее.

10. Построить поверхность .

Вариант 12.

1. Проверить, является ли система векторов линейно зависимой:

f₁=(3;-1;-2;1), f₂=(-4;1;0;0), f₃=(0;0;-4;-6).

Найти длину каждого вектора, определить координаты вектора .

2. Найти ранг матрицы .

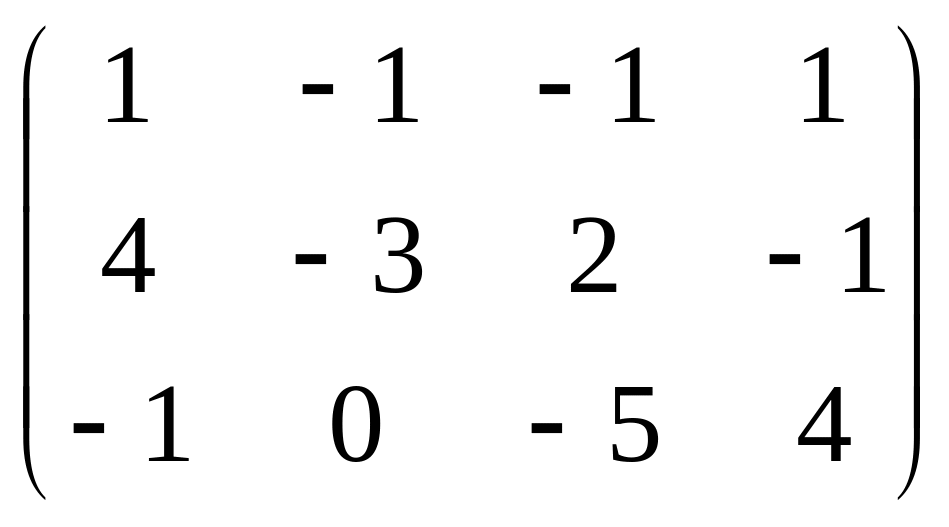3. Решить систему уравнений методом Гаусса

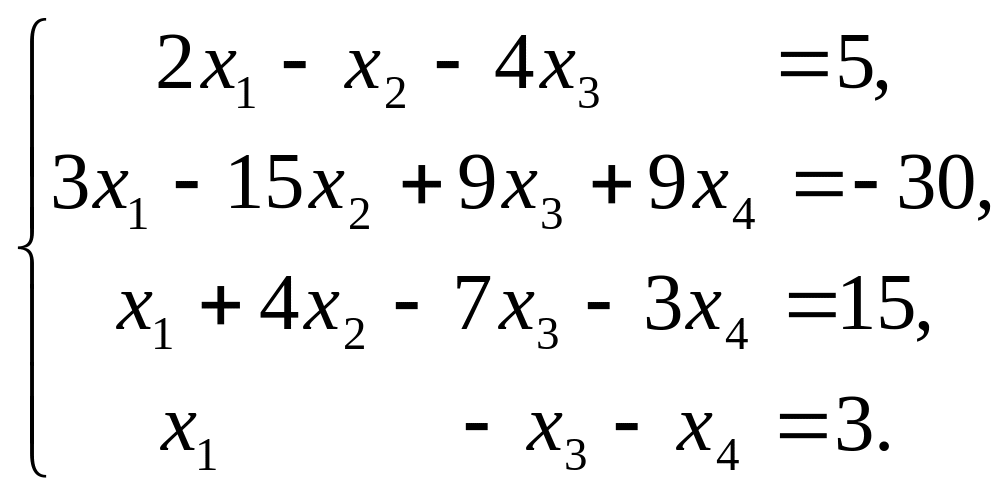
4. Вычислить определитель матрицы .

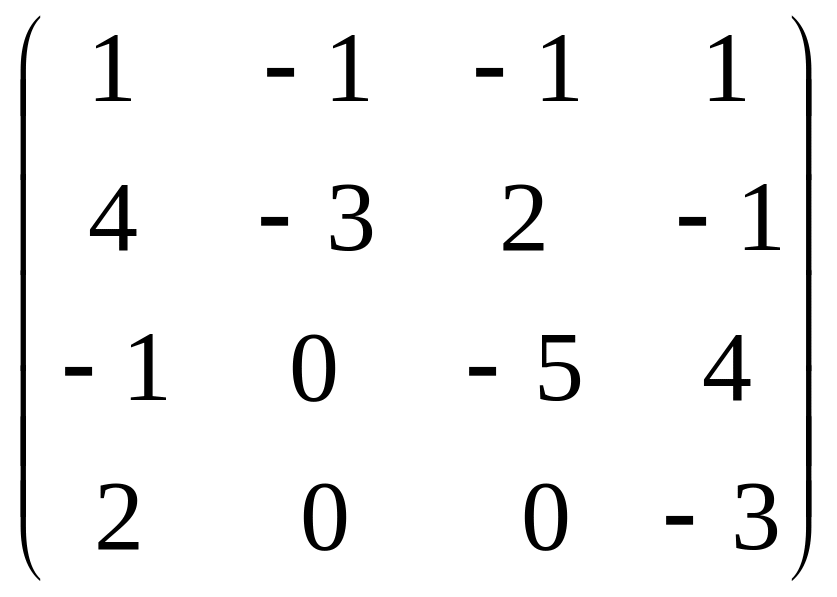5. Привести матрицу к каноническому виду .

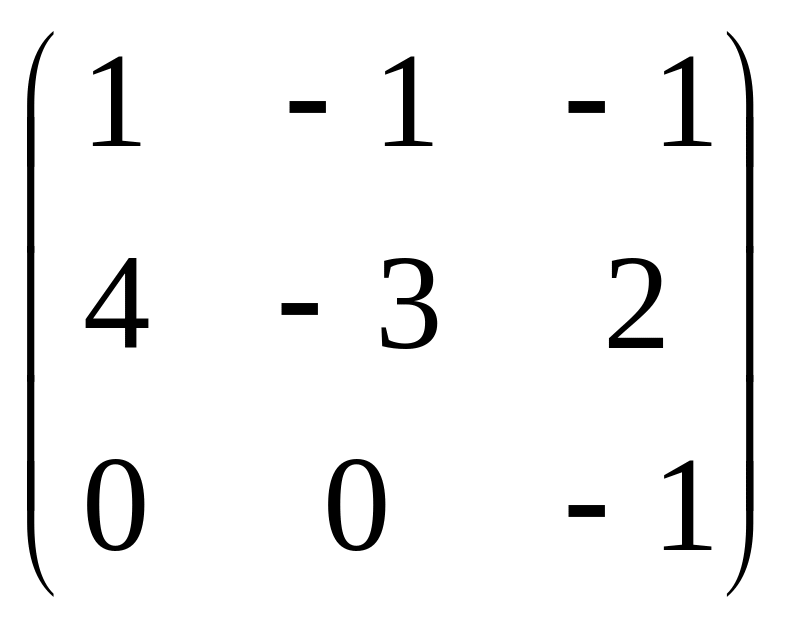6. Написать уравнение прямой, проходящей через заданные точки А(-8;-4), В(1;1). Построить эту прямую и привести уравнение к виду в отрезках на осях.

Написать уравнение пучка прямых, проходящих через А, и выбрать из пучка прямую перпендикулярную АВ.

7. Написать уравнение линии, которая при движении точки М остается равноудаленной от точки А(2;0) и от прямой . Построить ее.

8. Преобразовать к каноническому виду уравнение и построить кривую.

9. Написать уравнение плоскости, проходящей через точки А(-1;-2;0), В(1;1;2) и перпендикулярную к плоскости . Построить ее.

10. Построить поверхность .