Второй закон Ньютона

Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между равнодействующей всех приложенных к телу сил и ускорением этого тела. Один из трёх законов Ньютона. Второй закон Ньютона утверждает: в инерциальных системах ускорение, приобретаемое материальной точкой (телом), прямо пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела).Этот закон записывается в виде формулы: , где  — ускорение тела,  — сила, приложенная к телу, а  — масса тела, причём  — константа. Или, в более известном виде: в тех же обозначениях. В случае, если масса тела меняется со временем, то второй закон Ньютона записывается в общем виде (в таком виде его написал сам Ньютон): где  — импульс (количество движения) тела,  — время, а  — производная по времени. Второй закон Ньютона справедлив только для скоростей, много меньших скорости света и в инерциальных системах отсчёта.

Третий закон Ньютона

Этот закон объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой , а второе — на первое с силой . Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются. Современная формулировка: Материальные точки попарно действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:

Закон отражает принцип парного взаимодействия. То есть все силы в природе рождаются парами. Историческая: Действию всегда есть равное и противоположное противодействие, иначе — взаимодействия двух тел друг на друга равны и направлены в противоположные стороны.

Второй закон Ньютона для системы тел

Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между равнодействующей всех приложенных к телу сил и ускорением этого тела. Один из трёх законов Ньютона. Второй закон Ньютона утверждает: в инерциальных системах ускорение, приобретаемое материальной точкой (телом), прямо пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела).Этот закон записывается в виде формулы: , где  — ускорение тела,  — сила, приложенная к телу, а  — масса тела, причём  — константа. Или, в более известном виде: в тех же обозначениях. В случае, если масса тела меняется со временем, то второй закон Ньютона записывается в общем виде (в таком виде его написал сам Ньютон): где  — импульс (количество движения) тела,  — время, а  — производная по времени. Второй закон Ньютона справедлив только для скоростей, много меньших скорости света и в инерциальных системах отсчёта.

Центр масс системы тел

Центром масс системы называется точка С, положение которой задаётся радиусом-вектором r_c, определяемым следующим образом:

механике определяется следующим образом: где

 — радиус-вектор центра масс,

 — радиус-вектор i-й точки системы,

 — масса i-й точки. Для случая непрерывного распределения масс:

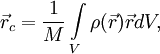
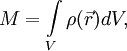где:

 — суммарная масса системы,

 — объём,

 — плотность. Центр масс, таким образом, характеризует распределение массы по телу или системе частиц.

Система отсчёта, в которой центр масс покоится, называется системой центра масс или ц-системой. Эта сист-ма инерциальна.

Закон сохранения импульса

. Выражение представляет собой уравнение движения частицы. Если его проинтегрировать, то можно найти траекторию частицы r = r(t, F). Однако часто это не является необходимым. Оказывается, уравнения Ньютона обладают тем свойством, что некоторые величины, характеризующие движение частицы, остаются неизменными во все время движения. О таких величинах принято говорить, что они сохраняются. Их также называют интегралами движения. Знание интегралов движения позволяет получить ряд важных следствий без фактического решения уравнений движения. Получим некоторые сохраняющиеся величины. Перепишем в виде . Величина называется импульсом тела. Внеся величину m под знак дифференциала в (1.26), закон Ньютона можно записать в форме: . Физический смысл импульса становится очевидным, если уравнение проинтегрировать на конечном интервале времени от 0 до t: . Изменение импульса служит мерой величины силы, действующей на тело в течение конечного промежутка времени. Численно величина импульса . Рассмотрим тело или систему тел в отсутствие внешних сил. Система тел, на которую не действуют внешние силы (или векторная сумма этих сил равна нулю), является замкнутой. В этом случае F=0; как видно из уравнений или . ,

, т.е. величина ,

остается постоянной во все время движения. Полученный результат представ­ляет собой закон сохранения импульса, который имеет место как для одного тела, так и для системы тел в отсутствие внешних сил.