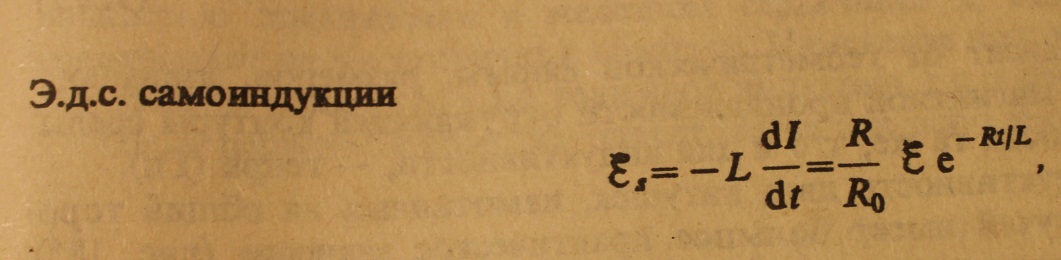8. Моментом силы относительно неподвижной оси z называется скалярная величина Mz , равная проекции на эту ось вектора м момента силы, определенного относительно произвольной точки о данной оси z:

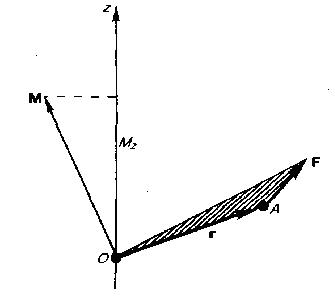
Найдем выражение для работы при вращении тела 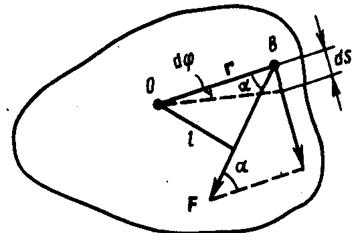Пусть сила F приложена в точке В, находящейся от оси z на расстоянии r, α - угол между радиусом-вектором r и направлением силы. Так как тело абсолютно твердое, то работа этой силы равна работе, которую необходимо затратить на поворот всего тела. При повороте тела на бесконечно малый угол dφ точка приложения В проходит путь ds=rdφ и работа равна произведению проекции силы на направление смещения на величину смещения:  (2)  можем записать    где Frsinα=Fl=M_z - момент силы относительно оси z. Значит, работа при вращении тела равна произведению момента действующей силы на угол поворота.  Работа при вращении тела идет на увеличение его кинетической энергии: dA=dT, но   поэтому  , или    Учитывая, что   получаем   (3)  Уравнение (3) представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси.  Можно показать, что если ось z совпадает с главной осью инерции, проходящей через центр масс, то имеет место векторное равенство :   где J - главный момент инерции тела (момент инерции относительно главной оси).

9. Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:    Используя формулу v_i = ωr_i, получим    т. е.        Эта формула - еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси.  В замкнутой системе момент внешних сил   и   откуда   

Моментом инерции системы (тела) относительно данной оси называется физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси:    В случае непрерывного распределения масс эта сумма сводится к интегралу:   где интегрирование производится по всему объему тела. При этом величина r есть функция положения точки с координатами х, у, z. В качестве примера будем искать момент инерции однородного сплошного цилиндра высотой h и радиусом R относительно его геометрической оси  

  Если мы знаем момент инерции тела относительно оси, проходящей через его центр масс, то мы можем найти и момент инерции относительно любой другой параллельной этой оси, который можно найти с помощью теоремы Гюйгенса-Штейнера: момент инерции тела J относительно произвольной оси равен моменту его инерции J_c относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы m тела на квадрат расстояния а между осями:   

Возьмем абсолютно твердое тело, вращающееся около неподвижной оси z, проходящей через него. Разобьем тело на маленькие объемы с элементарными массами m₁, m₂,..., m_n , находящиеся на расстоянии r₁, r₂,..., r_n от оси. 

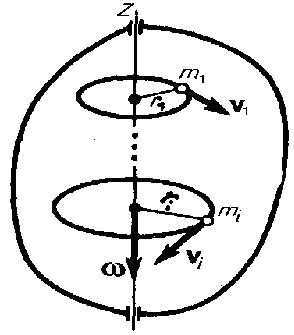
При вращении твердого тела относительно неподвижной оси каждый из его элементарных объемов массами m_i опишет окружность соответствующих радиусов r_i; при этом объем будет иметь соответствующую линейную скорость v_i. Но так как мы рассматриваем абсолютно твердое тело, то угловая скорость вращения этих объемов одинакова:  . Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов:   или     ,где J_z - момент инерции тела относительно оси z.

Таким образом, кинетическая энергия вращающегося тела :   Из сравнения этой формулы с выражением для кинетической энергии поступательно движущегося тела (T=mv²/2), мы видим, что момент инерции является мерой инертности тела при вращательном движении. Формула справедлива для тела вращающегося вокруг неподвижной оси.  В качестве примера напишем формулу для плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения. Его энергия движения складывается из энергии поступательного движения и энергии вращения:   ,где m - масса катящегося тела; v_c - скорость центра масс тела; J_c - момент инерции тела относительно оси, проходящей через его центр масс; ω - угловая скорость тела.

27. Как мы уже знаем, электрическое поле оказывает силовое воздействие как на неподвижные, так и на движущиеся в нем электрические заряды. У магнитного поля имеет важнейшая особенность состоит в том, что оно оказывает силовое воздействие только на движущиеся в этом поле электрические заряды.

Закон Био-Савара-Лапласа для проводника с током I, элемент dl которого создает в некоторой точке А индукцию поля dB, равен: , Модуль вектора dB задается выражением :  , где α — угол между векторами dl и r.  Аналогично электрическому, для магнитного поля выполняется принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:   

магнитная индукция поля прямого тока (рис.1, 2) :

       

Магнитное поле в центре кругового проводника с током. Как видно из рисунка, каждый элемент кругового проводника с током создает в центре магнитное поле одинакового направления - вдоль нормали от витка. Значит, сложение векторов dB также можно заменить сложением их модулей. Поскольку расстояние всех элементов проводника до центра кругового тока одинаково и равно R и все элементы проводника перпендикулярны радиусу-вектору (sinα=1):   

   

27. До сих пор рассматривалось магнитное поле, которое создавалось проводниками с током или движущимися электрическими зарядами, находящимися в вакууме. Если же магнитное поле создается не в вакууме, а в какой-то другой среде, то магнитное поле изменяется. Это объясняется тем, что различные вещества, помещенные в магнитное поле, намагничиваются и сами становятся источниками магнитного поля. Вещества, способные намагничиваться в магнитном поле, называются магнетиками. Намагниченное вещество создает магнитное поле с индукцией  , которое накладывается на магнитное поле с индукцией  , обусловленное токами. Оба поля в сумме дают результирующее поле, магнитная индукция которого равна: .

Физическая величина, показывающая, во сколько раз индукция магнитного поля в однородной среде отличается по модулю от индукции магнитного поля в вакууме, называется магнитной проницаемостью: , магнитная проницаемость зависит от рода вещества и от его состояния, например, от температуры.

Вещества крайне разнообразны по своим магнитным свойствам. У большинства веществ эти свойства выражены слабо. Слабомагнитные вещества делятся на две большие группы – парамагнетики и диамагнетики. Они отличаются тем, что при внесении во внешнее магнитное поле парамагнитные образцы намагничиваются так, что их собственное магнитное поле оказывается направленным по внешнему полю, а диамагнитные образцы намагничиваются против внешнего поля. Поэтому у парамагнетиков μ > 1, а у диамагнетиков μ < 1. Парамагнитные вещества магнитными свойствами не обладают, но всегда обладают магнитным моментом.

Существую сильномагнитные вещества – ферромагнетики – вещества, обладающие спонтанной намагниченностью, т.е. они намагничены даже при отсутствии внешнего магнитного поля. Ферромагнетики обладают существенной особенностью: для каждого ферромагнетика существует определенная температура, называемая точкой Кюри, при которой он теряет свои магнитные свойства. Природа ферромагнетизма может быть до конца понята только на основе квантовых представлений. Качественно ферромагнетизм объясняется наличием собственных (спиновых) магнитных полей у электронов. В кристаллах ферромагнитных материалов возникают условия, при которых, вследствие сильного взаимодействия спиновых магнитных полей соседних электронов, энергетически выгодной становится их параллельная ориентация. В результате такого взаимодействия внутри кристалла ферромагнетика возникают самопроизвольно намагниченные области размером порядка 10^–2–10^–4 см. Эти области называются доменами. Каждый домен представляет из себя небольшой постоянный магнит.

В отсутствие внешнего магнитного поля, направления векторов индукции магнитных полей в различных доменах ориентированы в большом кристалле хаотически. Такой кристалл, в среднем оказывается не намагниченным. При наложении внешнего магнитного поля   происходит смещение границ доменов так, что объем доменов, ориентированных по внешнему полю, увеличивается. С увеличением индукции внешнего поля возрастает магнитная индукция намагниченного вещества. В очень сильном внешнем поле домены, в которых собственное магнитное поле совпадает по направлению с внешним полем, поглощают все остальные домены, и наступает магнитное насыщение.

 всякий раз, когда в опыте осуществляется изменение сцепленного с контуром потока магнитной индукции, в контуре возникает индукционный ток; возникновение индукционного тока указывает на существование в цепи электродвижущей силы, которая называется электродвижущей силой электромагнитной индукции. Количественное значение индукционного тока, а значит, и э.д.с. электромагнитной индукции ξ_i задается только скоростью изменения магнитного потока, т. е.

 

На следующем шаге необходимо выяснить знак ξ_i . Знак магнитного потока задается выбором положительной нормали к контуру, а положительное направление нормали определяется правилом правого винта. Значит, выбирая положительное направление нормали, мы знаем как знак потока магнитной индукции, так и направление тока и э.д.с. в контуре. Пользуясь этими соображениями и выводами, можно прийти к формулировке закона электромагнитной индукции Фарадея: какова бы ни была причина изменения потока магнитной индукции, охватываемого замкнутым проводящим контуром, возникающая в контуре э. д. с. : Знак минус говорит о том, что увеличение потока (dФ/dt>0) вызывает э.д.с. ξ_i<0 т. е. направление поля индукционного тока навстречу потоку; уменьшение потока (dФ/dt<0) вызывает ξ_i>0 т.е. направления поля индукционного тока и потока совпадают. Знак минус задается правилом Ленца - общим правилом для нахождения направления индукционного тока, полученного в 1833 г. 

Правило Ленца: индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшему этот индукционный ток. 

Явление возникновения ЭДС индукции в электрической цепи в результате изменения силы тока в этой цепи называется самоиндукцией. В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.