
Обратная матрица. Условия существование.
Определение: А-1 называется обратной матрицей А, если выполняются условия A·A-1= A-1·A=E
Теорема: если для матрицы А существует обратная, то она единственная.
Теорема:
для того, чтобы для квадратной матрицы
А существовала A-1
необходимо и достаточно, чтобы определитель
 0.
Т.е. перед началом вычислений нужно
найти определитель.
0.
Т.е. перед началом вычислений нужно
найти определитель.
Свойства ОМ:
(A-1) -1 = А
(А·B) -1 = B-1·A-1
Условие существования
обратной матрицы. Для того,
чтобы квадратная матрица A имела
обратную, необходимо и достаточно, чтобы
она была невырожденной, т.е. det A ≠
0. ,при этой обратная матрица
определена однозначно и ей можно найти
по формуле
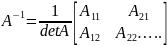

Метод обратной матрицы
решения систем линейных алгебраических
уравнений с ненулевым определителем
основной матрицы состоит в поиске
матрицы, обратной к основной матрице,
и умножению ее на матрицу свободных
членов.
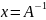 B
B
Метод Гаусса- метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные. Элементарные преобразования : перестановка любых двух строк матрицы; умножение любой строки на произвольное, отличное от нуля, число; сложение любой строки с другой строкой , умноженной на произвольное число;
Ранг матрицы и его вычисление.
Рангом системы строк (столбцов) матрицы A с m строк и n столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.
Рангом матрицы называется наибольший из порядков миноров матрицы, отличных от нуля. Ранг нулевой матрицы считается равным нулю. Ранг невырожденной квадратной матрицы порядка равен, так как ее определитель является минором порядка и у невырожденной матрицы отличен от нуля.
Рассмотрим прямоугольную матрицу. Выделим в этой матрице k произвольных строк и k произвольных столбцов (k≤n, k≤m). Определитель k-го порядка, составленный из элементов матрицы А, расположенных на пересечении выделенных строк и столбцов, называется минором k-го порядка матрицы. Так, у матрицы с тремя строками и пятью столбцами возможны миноры первого, второго и третьего порядка. Рангом матрицы А (обозначается r(A)) называется наибольший порядок минора этой матрицы, отличного от нуля. Если все элементы матрицы равны нулю, то ранг такой матрицы принимают равным нулю.
Всякий отличный от нуля минор матрицы, порядок которого равен рангу этой матрицы, называется базисным минором матрицы. Ранг матрицы не изменится от следующих преобразований, называемых элементарными преобразованиями матрицы: - замены строк столбцами, а столбцов соответствующими строками; - перестановки строк матрицы; - вычеркивания строки, все элементы которой равны нулю; - умножения строки на число, отличное от нуля; - прибавления к элементам строки соответствующих элементов другой строки, умноженной на одно и то же число. Сама матрица при элементарных преобразованиях меняется, но ранг матрицы не изменится.
(Теорема о базисном миноре).
Базисные строки (базисные столбцы) линейно независимы. Любая строка (любой столбец) матрицы A является линейной комбинацией базисных строк (базисных столбцов).
Доказательство. Все рассуждения приведём для строк.
Независимость базисных строк будем доказывать от противного. Пусть базисные строки линейно зависимы. Тогда по теореме 1 одна из строк является линейной комбинацией остальных. Но тогда из свойств определителя вытекает, что базисный минор равен нулю, чего не может быть, следовательно, базисные строки линейно независимы.
Докажем
теперь, что любая строка матрицы
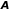 является линейной комбинацией базисных
строк. Не нарушая общности, можно считать,
что базисный минор расположен в левом
верхнем углу матрицы
.
Рассмотрим определитель
является линейной комбинацией базисных
строк. Не нарушая общности, можно считать,
что базисный минор расположен в левом
верхнем углу матрицы
.
Рассмотрим определитель
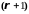 -го
порядка вида:
-го
порядка вида:
 ,
,
полученный
добавлением к базисному минору частей
любой
 -й
строки и любого
-й
строки и любого
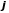 -го
столбца матрицы
.
Докажем, что
-го
столбца матрицы
.
Докажем, что
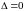 .
Если
.
Если
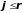 и
и
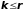 ,
то
,
так как он содержит два одинаковых
столбца или две одинаковых строки. Если
,
то
,
так как он содержит два одинаковых
столбца или две одинаковых строки. Если
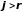 и
и
 ,
то
,
то
 - есть минор (
- есть минор (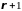 )-го
порядка матрицы
,
а всякий такой минор равен нулю.
)-го
порядка матрицы
,
а всякий такой минор равен нулю.
Итак,
.
Разлагая
по элементам последнего столбца и
обозначая алгебраические дополнения
элементов
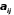 буквами
буквами
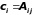 ,
получим
,
получим
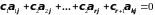
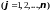 .
Но
.
Но
 равно базисному минору, поэтому
равно базисному минору, поэтому
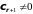 .
Отсюда, обозначая
.
Отсюда, обозначая
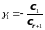 ,
,
 ,
…,
,
…,
 ,
из последнего равенства получим:
,
из последнего равенства получим:
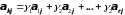 ,
а это означает, что любая
-я
строка матрицы
является линейной комбинация базисных
строк. Теорема доказана.
,
а это означает, что любая
-я
строка матрицы
является линейной комбинация базисных
строк. Теорема доказана.
Правило Крамера 1
Для
простоты выкладок рассмотрим систему
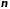 линейных алгебраических уравнений с
неизвестными, положив
линейных алгебраических уравнений с
неизвестными, положив
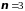
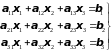 .
.
Пусть
определитель этой системы отличен от
нуля, т.е.
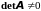 .
Тогда можно записать решение этой
системы в матричном виде, положив
.
Тогда можно записать решение этой
системы в матричном виде, положив
 .
.
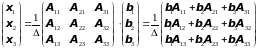 .
.
Следовательно,
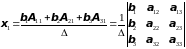


Полученные
формулы для вычисления
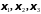 называются формулами Крамера,
а соответствующее правило – правилом
Крамера. Итак, если определитель
системы
линейных алгебраических уравнений с
неизвестными
отличен от нуля, то по формулам Крамера:
называются формулами Крамера,
а соответствующее правило – правилом
Крамера. Итак, если определитель
системы
линейных алгебраических уравнений с
неизвестными
отличен от нуля, то по формулам Крамера:

 ,
где определитель
,
где определитель
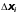 получается из определителя системы
путём замены
получается из определителя системы
путём замены
 -го
столбца столбцом из свободных членов.
-го
столбца столбцом из свободных членов.
