Сплайны

Многоинтервальная интерполяция заключается в том, что значение функции , определяется в ряде промежуточных узлов на широком интервале с помощью полиномов невысокой степени.

Применение полиномов высокой степени на выбранном интервале приводит к большему объёму вычислений и не обеспечивает высокой точности. Наиболее распространенны:

1. простой способ – это применение кусочно – линейной интерполяции при равномерном расположении узлов.

Имеем: шаг и , для функции . Вычисления функции

где .

Обычно степень полинома росла вместе с числом узлов, здесь – не зависит. Уменьшение монотонно снижает погрешность интерполяции, но массив растёт. Формула неизменна.

2. Квадратичная интерполяция – требует чётного числа парных интервалов (n – чётное число).

Имеем: , - шаг, и массив .

Если использовать формулу Лагранжа для трёх ординат, то получим

где и +1

В узлах i значения y(x) и совпадают.

3. Кубическая интерполяция (также локальная) - это интерполяция полинома третьей степени.

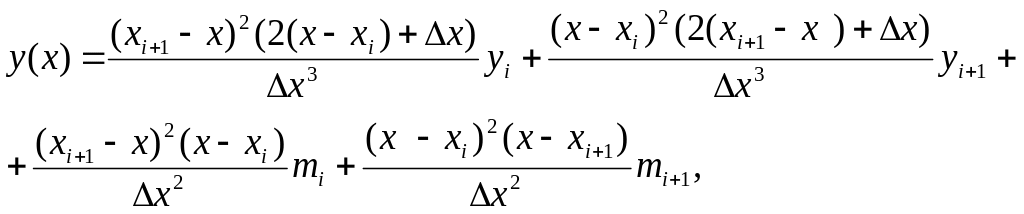
Где , - первые производные y(x)

Производные могут вычисляться с помощью формул численного дифференцирования по трём точкам:

Матрицы

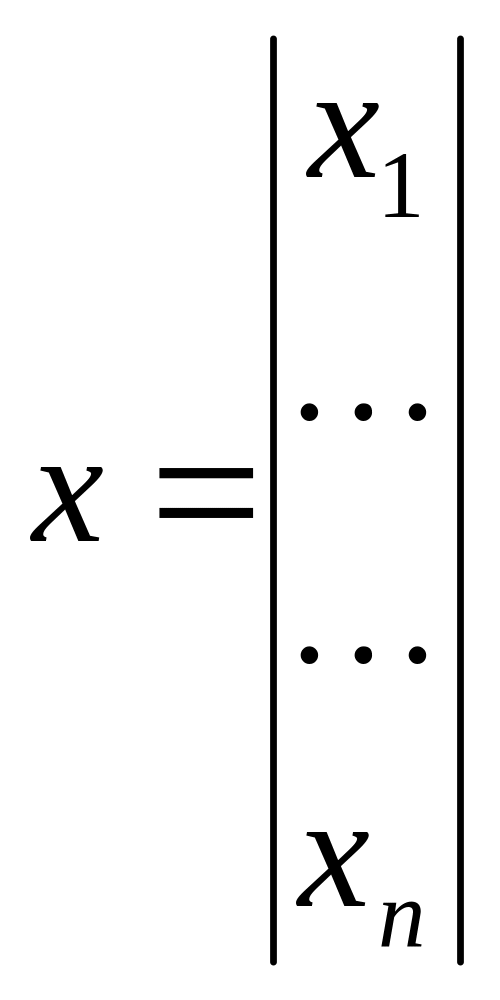
Вещественное число-скаляр. Будем обозначать греческими буквами. Упорядоченный набор скаляров вектор. Вектор столбец где n- размер вектора. Если совпадают все компоненты вектора (размерность их должна совпадать). Вектор строка

направление упорядочения сверху вниз и слева направо. Если упорядочить 2-х мерный массив чисел, то получим матрицу.

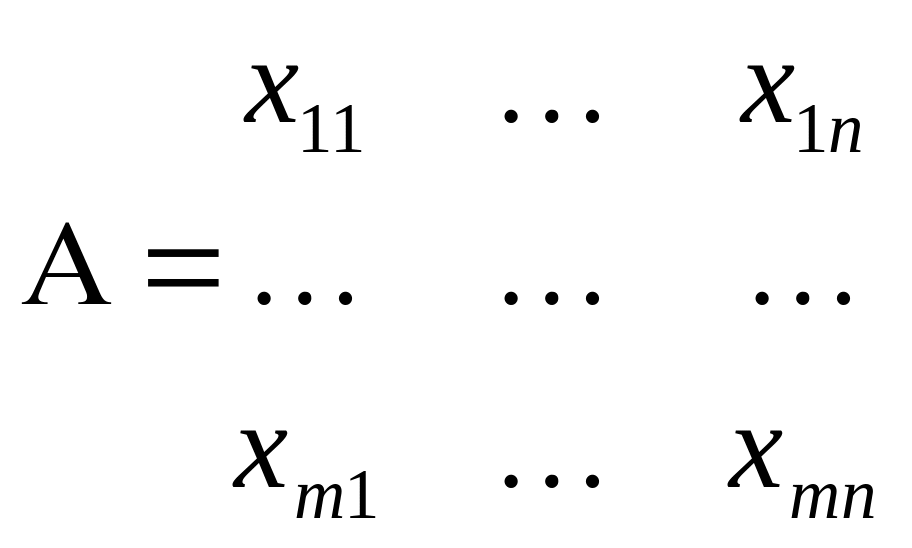
m-размерность по строкам

n-размерность по столбцам

Вектор-столбец и вектор-строка – частные случаи матрицы. Матрицы равны если совпадают все элементы ,т.е. , .

Если в матрице А столбцы и строки поменять местами, то получим транспонированную матрицу . В # .Матрица симметрична, если . Это обязательно квадратная матрица, т.е. m=n. Матрица с называется диагональной. Если в диагонали 1 ,то это единичная матрица E.

Нулевая матрица. Элементы для которых -наддиагональные, а поддиагональные.

1. Умножение матриц на число: (вектора на число).

2. Сложение матриц (векторов):

C=A+B.

A+(B+C)=(A+B)+C- ассоциативность.

A+B=B+A- коммутативность.

Для двух векторов a и b существует понятие скалярного произведения

Его можно рассматривать как .Его свойства:

-коммутативность.

-дистрибутивность.

Два ненулевых вещественных числа всегда имеют не нулевое произведение. Векторы же ненулевые могут дать при преумножении скалярное произведение равное 0.

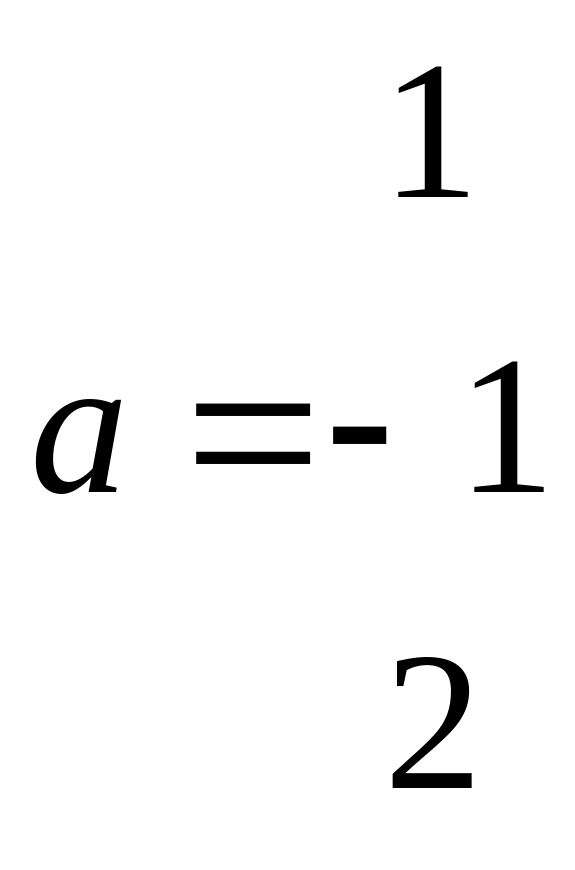
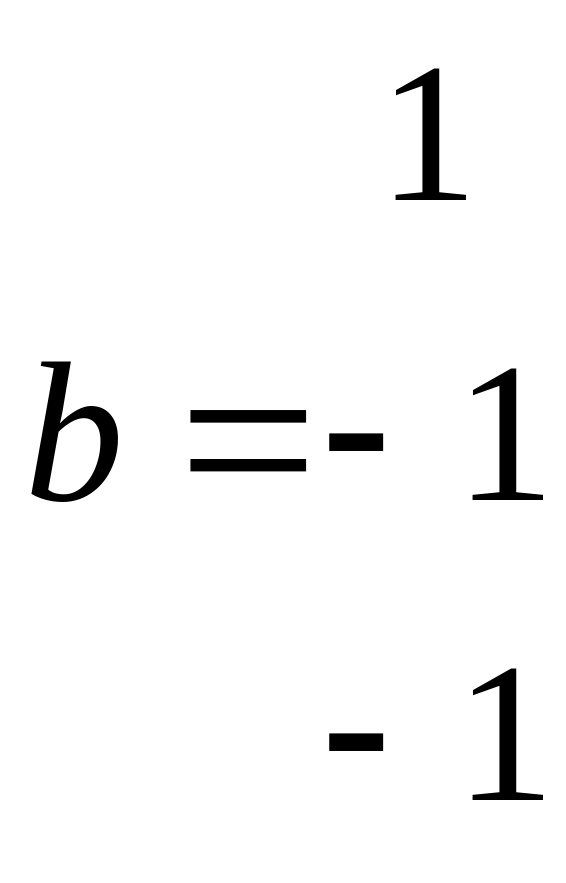
В этом случае векторы ортогональны друг другу.

Если ,то отсюда не следует равенство a=b.

В силу дистрибутивности можно утверждать ,что вектора a-b и с ортогональны. Нулевой вектор ортогонален всем прочим векторам. Обобщение понятия скалярного произведения –это операция перемножения матрицы:C=AB.Матрица С определяется как скалярное произведение i-строки А на j-столбец B. Число строк матрицы B должно соответствовать числу столбцов матрицы А.

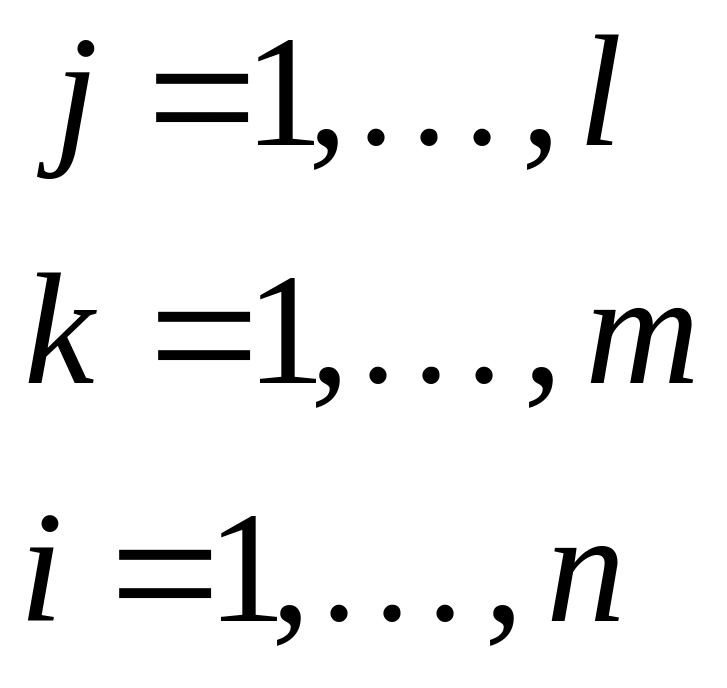
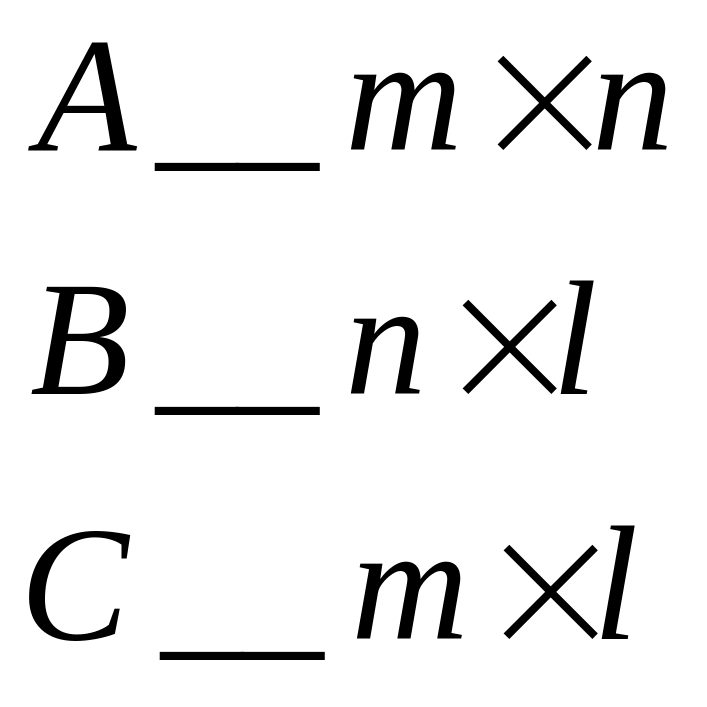
Если обозначить строку матрицы ,

а столбец матрицы , то

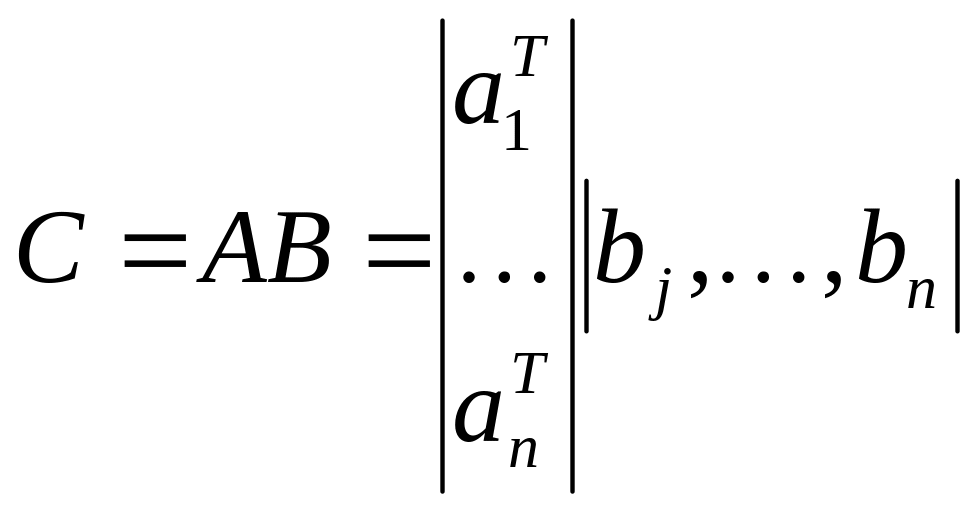
Свойства:

- не коммутативность

-ассоциативность

- дистрибутивность.

Возможны следующие комбинации векторов и матриц при умножении:

1. Матрица А на матрицу В = матрица.

2. Матрица А на столбец В = столбец

3. Строка А на матрицу В = строка.

4. Строка А на столбец В = скаляр.

5. Столбец А на строку В = матрица.

Алгоритм умножения матриц:

Procedure UmnMat (Var a,b,c:mat; Var M,N,L:integer);

Var k,I,j:integer;

Var s:rial;

Begin

For k:=1 to M do

For j:=1 to L do

Begin s:=0;

For i:=1 to N do

S:=s+A[K,I]*B[I,J];

C[K,J]:=S

End;

End.

Все варианты можно реализовать с помощью этой процедуры

UmnMat(A,B,C,M,N,L);

Когда размерность матрицы А ,а матрицы В ,получим матрицу С размером

,т.е. реализован общий случай 1.

Если L=1, то реализован случай 2. и результат имеет вид столбца .

Если , то имеем 3-й случай и результат будет строка .

Если и ,то имеем 4-й случай и результат будет скаляр в

Если ,то имеем 5-й случай А и В ,а С ,т.е. матрица.

Иные варианты сомножителей возможны, если их удастся привести к рассмотренным комбинациям.

Порядок написания m,n,L как фактических параметров при обращении к процедуре

UmnMat должен быть с учётом сказанного, поскольку параметры циклов жёстко связанны с параметрами m,n,L.

Многомерная оптимизация

1) f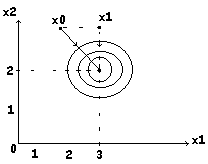 (x)=(x₁ –3)² +(x₂ –2)²-5

f(x)=grad f(x)=(2x₁-6 , 2x₂-4);

G (x)= 2 0

0 2

Окружности – линии равного уровня для f(x)

Пунктиром показаны траектории поиска экстремума покоординатным

методом.

Сплошная линия – траектория наискорейшего спуска.

Число обусловленности – отношение max собственного значения к min собственному значению (Ц=1)

(Шарик катится на дно по прямой).

2) f(x)=(x₁ –5)² +9(x₂ –2)²-9

f(x)=(2x₁-10 , 18x₂-36);

G (x)= 2 0 Ц=18

0 2

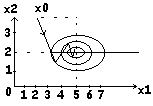Овраг направлен вдоль одной из осей и проблем поиска экстремума не возникает, но процесс наискорейшего спуска перестал быть таковым.

(Шарик катится на дно, переваливаясь с одного склона на другой)

Число обусловленности еще не чрезмерно велико.

А если овраги узки и извилисты, то методы (оба) могут зайти в тупик.

3. Для узкого оврага

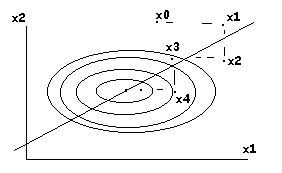
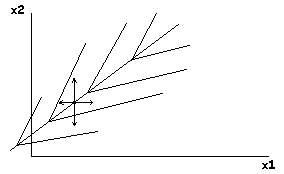
_{Овраг не сориентирован вдоль координатных осей. Любое движение по осям координат не дает успеха}

T:=T/2 /(W-2*V+U);

If (T-Z)<E then

begin

write (‘x min=’ , T);

end;

Z:=T; goto 1;

end;

Результат вычисления процедуры FUNK содержится в идентификаторе F , который является параметром процедуры.

Входным параметром процедуры FUNK является X.

Перед обращением к процедуре KWADRIN необходимо задать значение X1. Этот параметр должен быть глобальным по отношению к этой процедуре, т.е. его следует задать и описать в основной программе.

Существуют методы, аппроксимирующие функцию f(x) кубическим полиномом. В иностранной литературе метод квадратичной интерполяции называется методом Пауэла, а кубической – Давидсона.