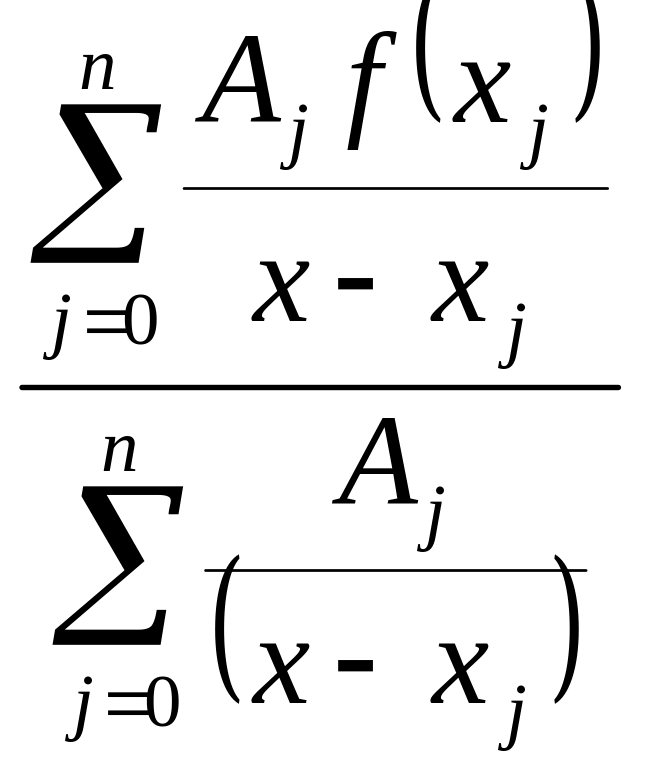- •Т.О., если определен корень характеристического уравнения, то можно понизить на единицу степень полинома и приступить к решению уравнения:
- •Идентификаторы совпадают для переменных: .
- •Приближенное значение производной можно записать: т.К. , то далее процесс итераций х следует повторить до достижения величиной заданной точности е. В общем виде алгоритм запишется :
- •1. Какие узлы использовать.
- •Интерполяционные полиномы Эрмита
- •Сплайны
- •Методы поиска экстремума функции многих переменных.
- •Метод покоординатного спуска (Гаусса – Зейделя)
- •Метод прямого поиска (конфигураций).
- •Градиентные методы.
- •Наискорейший спуск
- •Метод дфп
1. Какие узлы использовать.
2. Какой класс приближенных функций использовать.
3. Какой критерий согласия будет применён.
4. Какая точность требуется.
1. Чаще всего используются равноудалённые узлы.
2. а. В инженерных расчётах обычно используют прямую, либо квадратичную
параболу. Реже
многочлены более высокой степени, т.е.
используют линейные комбинации
![]()
б. Гармонические
функции:
![]() sin
sin
![]() -
этот класс используют в рядах и интегралах
Фурье;
-
этот класс используют в рядах и интегралах
Фурье;
в. Показательные
функции -
![]() .
.
3. Точное соответствие (совпадение в узлах).
4. Совпадение результатов до 3, 4 знаков.
Б. Кроме аналитического “представления” таблиц, мы уже рассмотрели представление графической информации. Т.е. это два главных применения интерполяционных формул. Наряду с задачей определения значений между узлами столь же актуальна задача определения значений функции за одним из граничных узлов (левым или правым), где сетка
е щё
не сформирована. В этом случае можно
говорить об экстраполяции функции. При
этом используются обычные формулы
интерполяции.
щё
не сформирована. В этом случае можно
говорить об экстраполяции функции. При
этом используются обычные формулы
интерполяции.
При использовании граничных условий (при численном решении уравнений в частных производных) приходится использовать различные формулы (схемы) интерполяции для сохранения точности вычислений (вперёд, назад, центральные).
Указанная задача может усложнится, если требуется “прослеживать” в процессе расчётов перемещения границы расположения различных сред в динамике, т.е. во времени. Например, в газовой динамике необходимо определять расположение скачка уплотнения и его перемещение. Сказанное относится к математическим моделям, описанным дифференциальными уравнениями в частных производных. “ Передний фронт” вычислительной математики в настоящее время располагается в сфере таких задач. Если дифференциальные уравнения обыкновенные, не имеют пространственного измерения, у них одна независимая переменная – время, то для выше указанных классов задач характерна двух – трёхмерная постановка задач.
Чаще такие математические модели принадлежат объектам управления. Но и среди элементов систем управления есть такие, которые описываются уравнениями в частных производных.
Соответственно и интерполяция требуется по двум – трём координатам.
Рассмотрим задачу интерполяции в такой постановке, Имеем
![]()
1. Пусть известное
значение
в точках:![]() .
Тогда легко получить систему уравнений
(в n+1 точке)
.
Тогда легко получить систему уравнений
(в n+1 точке)
![]()
![]()
![]()
![]()
Система имеет
решение относительно
![]() ,
т.к. определитель Вандермонда
,
т.к. определитель Вандермонда
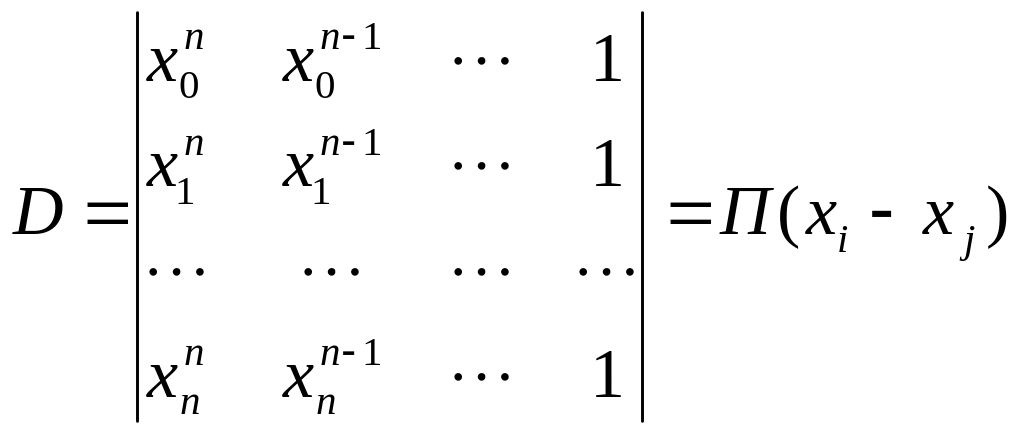 где
где
![]()
отличен от нуля
при всех
![]() (нет двух равных строк). Задача имеет
множество решений. Аналитическое
выражение
получено, но выбор точек произволен.
(нет двух равных строк). Задача имеет
множество решений. Аналитическое
выражение
получено, но выбор точек произволен.
2. Можно потребовать, чтобы многочлен
степени n (f(x))
проходил через фиксированные точки
![]() (равноотстоящие и не равноотстоящие).
Введём понятие – разделённые разности
– это разности функций в некоторых
точках отнесённые к разности аргументов
в этих точках:
(равноотстоящие и не равноотстоящие).
Введём понятие – разделённые разности
– это разности функций в некоторых
точках отнесённые к разности аргументов
в этих точках:
![]()
|
f(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Удобно разности функции получать в соответствии с таблицей. Затем берётся отношение к разности аргументов.
Метод интерполяции Лагранжа.
Рассмотрим функцию:
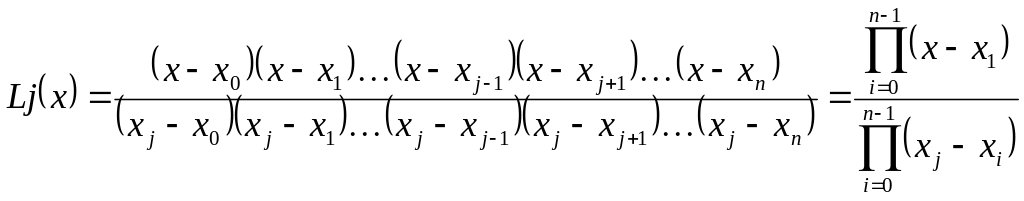
Она принимает
значение 1 в точке
![]() и 0 когда
и 0 когда
![]() в точке
в точке
![]() .
Поэтому многочлен
.
Поэтому многочлен
![]() проходит через узловые точки.
проходит через узловые точки.

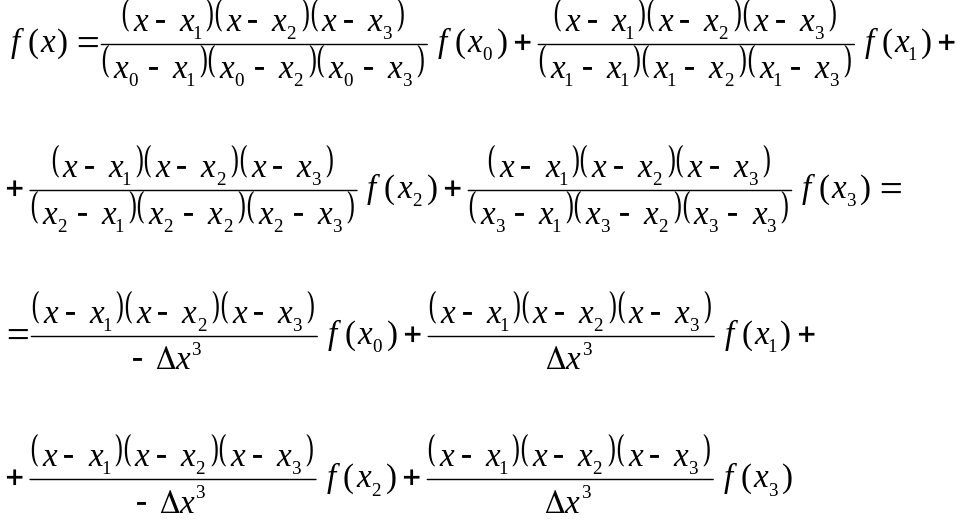
Допустим
![]() ,
тогда
,
тогда
![]() .
Возможны следующие пути исследования
формулы:
.
Возможны следующие пути исследования
формулы:
а. использование “в лоб”.
![]()
Полином 3-й степени.
б. использование
“барицентрической формулы”. Разделим
правую часть формулы Лагранжа на
![]() ,
т.к. f(x)=1,
если все
,
т.к. f(x)=1,
если все
![]()
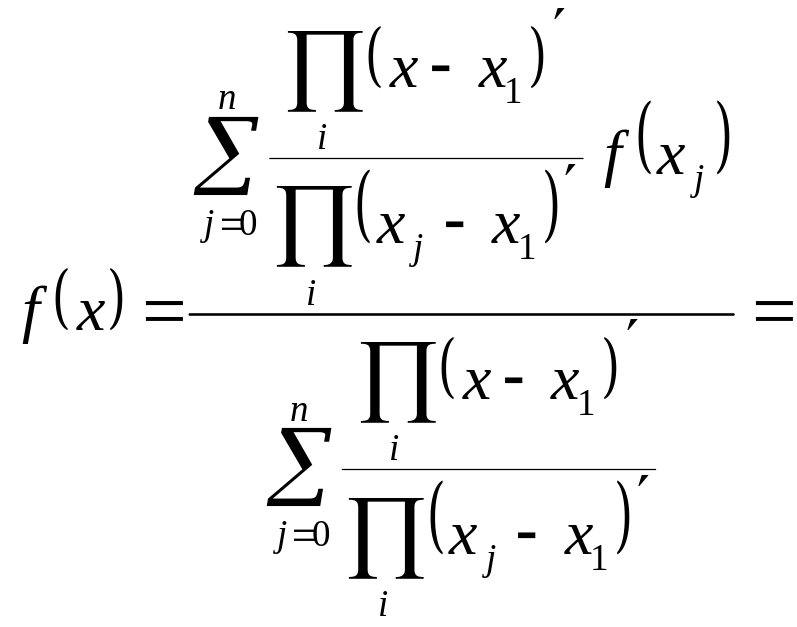 обозначим
обозначим
![]() =
=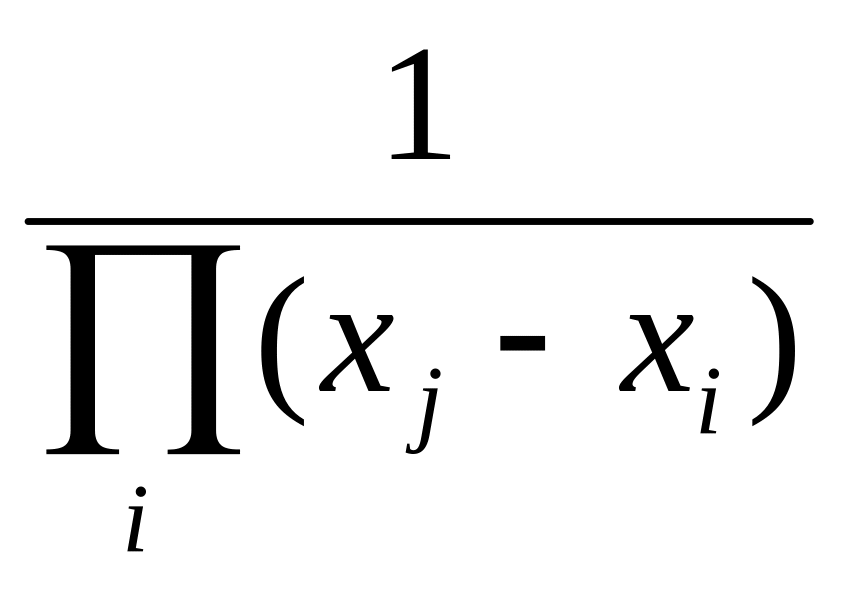 ,
поделим числитель и знаменатель на
,
поделим числитель и знаменатель на
![]() ,
получим кроме (i
,
получим кроме (i![]() j)
=
j)
=