Криволинейный интегралы. Формула Грина

П

34

усть точка P(x,y) движиться вдоль плоской линии L от М к точке N. К точке P приложена сила F которая изменяется по мере перемещение точки вдоль кривой то сила F представляет собой некоторую функцию от координат точки P F=f(p) выполняя работу А которая совершает сила F при передвижении от М к точке N.

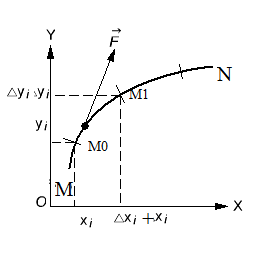Р азобьем кривую МN на n частей с помощью точек M0 M1 Mn обозначим через вектор велечину F в точке обозначим тогда скалярное произведение на можно рассмотреть как приближенное значение А если F вдоль дуги

Если существует придел выражение стоящего в правой части когда ->0 ( ->0 ->0) то этот придел выражает работу силы F при перемещении от М к N

этот придел называют криволинейным интеграл вдоль кривой L подобное ворожение часто встречается в математике при x и y расмотрении функции 2 переменных ограниченной в области D. буквы М и N стоят в место предела интегрированиявзяты в скобки в знак того что это не числа а обозночение криаой линии в доль которой ведеться интегрирование.

Направление в доль кривой от точки М к N называют непрерыным интервалом.

Если кривая L в пространстве то аналогичным оброзом задаеться криволинейный интеграл 3 функций Х(xyz) Y(xyz) Z(xyz)

Замечание

криволинейный интеграл зависит от 3 параметров кривой интегрирования функции и направления интегрирования. в частности при изменении направления интегрирования криволинейного интеграла меняется знак.

Разобьем кривую L точкой К то что дуга MN=MK+KN тогда

определение криволинейного интеграла остается в силе и в том случае когда кривая l является замкнутой в этом случае начало и конец точки совпадает для обозначения криволинейного интеграла по замкнутой линии используют обозначение

Вычисление криволинейного интеграла функции

Функция L рассмотрим правильный интеграл справедлива теорема о существовании криволинейного интеграла. Если функция являються интегрируемими и имеют непрерывные производные а также интервал функции как функцию от переменой t тода существует придел где -координаты некоторой точки на дуге эти приделы ни зависят от способа деления L на части дуги ни от выбора точек

Э

34

ти приделы А и В называют правильным интегралами и обозначают А= В= на основе этой теоремы можно получить формулу для вычисления криволинейного интеграла

пример вычислим криволинейный интеграл М(3,2,1) N(0,0,0)

уравнение прямой MN составляем параметрическое

(смотри координаты M и N)

Формула Грина

Эта формула устанавливает связь между двойным интегралом по области D и криволинейным интегралом по ее границе L пусть данной кривой облостьи D ее проекция на облость OX это отрезок ab с верху с низу в месте кривые отрожают замкнутый контур пусть в облосте D задана непрерывные функции X(xy) Y(xy) и имеют непрерывные частные производные. вычислить двойной интеграл по области D

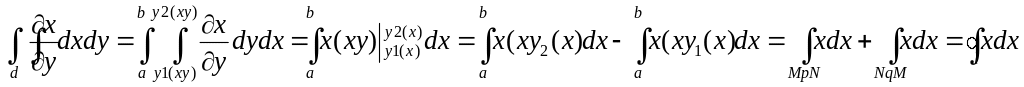
анологично и для y затем мы получаем формулу Грина