Комплексные числа

К

30

омплексным числом называют выражение вида a+bi, где a и b действительные числа а i мнимая единица a-действительная часть комплексного числа

b-коэффициент мнимой части a=rtz b=Inz

z=2+3i a=2 b=3 если а=0 z=bi- чисто мнимой части b=0 z=a -действительное число

Правило равенства. Два комплексных числа равны тогда и только тогда, когда равны их действительные части и равны коэффициенты мнимых частей.

тогда и тока тогда когда а=0 и b=0

два комплексных числа называют числа отличающихся тока знаком мнимой части называют сопряженной.

соответствует точки А(a,b). Существует взаимодействие между комплексными числами и точкой на плоскости.

тригонометрическая формула комплексного числа.

- треганаметрическая формула

f-аргумент для сопряженных

Сложение и вычитание

Умножение

Деление

возведение в степень

пример

Производная суммы, производная частного. Производная сложения

п

2

роизводная сумы равна сумме производных

Производная произведения

Производное частного

Общий вид первообразных. Первообразная функция. Понятие неопределенного интеграла.

Ф

13-15

ункция M(x)-первообразная от функции f(x) на отрезке AB если выполняется равенство м'(x)=f(x) для всех x этого отрезка.

Теорема

Если F(x) первообразная функции f(x) то функция F(x)+С (С-константа) тоже будет первообразной от f(x) Доказательство F(x)+C =f(x)+C'=f(x)

Если у нас будет F(x) и G(x) первообразные для f(x) тогда F(x)-G(x)=C Доказательство

найдем производную разности (F(x)-G(x))' = F(x)'-G(x)'=f(x)-f(x)=0-> F(x)-G(x)=-константе

Определение множество всех первообразных для функций f(x) называются неопределенным интегралом этой функции и обозначаются

Свойства не определенного интеграла, исходящие из определения. Правила интегрирования. Таблица интегралов.

Свойство неопределенного интеграла

Метод замены переменой в неопределенном интеграле

Если функция f(x) не прерывна а функция имеет непрерывную производную

то имеет место формула где

Пример

Интегрирование иррациональных функций

н

18-19

е от всякой иррациональной функции интеграл выражается через элементарные.

мы будем рассматривать только те иррациональные функции которые с помощью замены переменой приведуться к рациональным интеграл к виду где R рациональная функция. пусть k-общий общий знаменатель дробей сделаем подстановку тогда тогда наша дробная степень выразиться через целую степень t и подынтегральная функция преобразуется в рациональную.

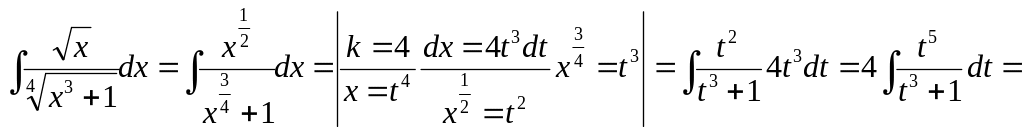(делим столбиком чтобы получить правильную дробь и получаем)

Интеграл вида этот интеграл сводиться к рациональному интегралу от рациональной функции с помощью подстановки где К общий знаменатель дроби

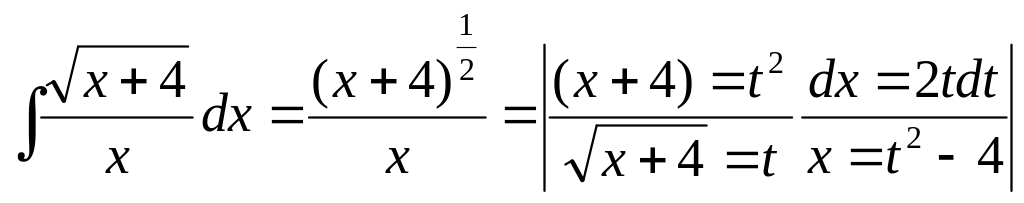
Интеграл вида где такой интеграл сводиться к интегралу от иррациональной функции с помощью одной из подстановок Эйлера.

Подстановка Эйлера

Если a>0 то берем все в квадрат -> dx=

=

Если С>0 то полагаем что

Если a<0 (D>0 ) , а подкоренное выражение раскладывается на действительные множители a(x – x₁)(x – x₂), то интеграл вида   рационализируется подстановкой  

Определенный интеграл и его свойства

Н

21

а отрезке AB задана некая функция f(x) будем считать что эта функция не прерывна. выберем на отрезке АВ произвольным образом точки x1 x2 x3 xn-1 так что они удовлетворя условие А<x1<x2...<Xn-1<b эти точки разбивают отрезок АВ на равные отрезки [A;x1] [x1;x3] ..в внутри каждого выберем произвольную точку С1 [A,x1] Сn [xn-1;b] обозначим разность -Интегральная сумма

Геометрический каждая слагаемое это сумма представляет собой площадь прямоугольника.

Значение интегральной суммы зависит от способа разбиения отрезка АВ и от выбора точек Сi

параметр разбиения не зависит от способа разложения если он существует и называется определенным интегралом функции f(x) на [a,b] a -нижний предел интегрирования b-верхний придел интегрирования [ab]

Разобьем отрезок [ab] на n отрезков частей тогда на каждом отрезке выберим точку i=1,2,3,4..