Решение типовой задачи.

Задача. Дана функция

Провести ее исследование на возрастание, убывание, экстремумы, выпуклости, вогнутость и точки перегиба.

Решение. Используем правила 1 и 2.

1. Область определения функции ]-∞,+ ∞[.

2. Найдем

3. Составим уравнение

Получим квадратное уравнение x²-3x-10=0. Корни этого уравне­ния x₁=-2 и x₂= 5 являются критическими точками.

4. Разбиваем область определения функции критическими точками на интервалы монотонности: ]-∞,-2[; ]-2,5[; ]5,+∞[.

5. Выбираем в каждом интервале произвольную точку и определяем в ней знак производной: f'(-3)>0; f'(0)<0; f'(6)>0.

6. Из теоремы 2 следует: на первом и третьем интервалах функция возрастает, а на втором - убывает.

7. Из теоремы 4 следует, что в точке x=-2 функция имеет максимум: y_max=f(-2)= . В точке x=5 функция имеет минимум: y_min=

8. Найдем y"=

9. 2x-3=0, x=3/2.

10. Точка x=3/2 - разбивает область определения на два интервала: ]-∞,3/2[ и ]3/2,+∞[

11. Найдем знак второй производной в произвольных точках этих интервалов f"(0)<0; f"(2)>0

12. На основании теоремы 5 делаем вывод: на интервале]-∞,3/2[график функции выпуклый, а на интервале]3/2,+∞[- вогнутый.

13. На основании теоремы 6 получаем: при переходе через точку x=3/2 вторая производная меняет знак. Это значит, что x=3/2 является абсциссой точки перегиба графика. Ордината точки перегиба f(3/2)= -13/4.

4. Функция многих переменных

В данном разделе ограничимся, в основном, рассмотрением функции двух аргументов.

Определение 1. Переменная Z называется функцией двух аргументов x и y, если некоторым парам значений (x,y) по какому-либо правилу или закону ставится в соответствие определенное значение Z. Обозначение: Z=f(x,y).

Определение 2. Множество пар значений, которые могут принимать аргументы x и y, называются областью определения функции.

Рассмотрим функцию Z=f(x,y) и дадим приращение аргументу x, оставив y без изменения. Получим точку (x+∆x,y), значение функции в этой точке f(x+∆x,y).

Определение 3. Разность f(x+∆x,y)-f(x,y)=∆_xf(x,y) или ∆_xZ называется частным приращением функции по аргументу x.

Аналогично разность f(x,y+∆y) - f(x,y)=∆_yf(x,y)= ∆_yZ называется частным приращением функции по аргументу y.

Если изменить оба аргумента, то получим значение функции f(x+∆x,y+∆y), а разность f(x+∆x,y+∆y)-f(x,y)= ∆f(x,y)= ∆Z - полное приращение функции Z=f(x,y).

Определение 4. Частной производной (первого порядка) функции Z=f(x,y) по аргументу x в точке (x,y) называется предел, если он существует, отношения частного приращения функции по аргументу x к приращению этого аргумента, при условии, что ∆x→0:

Z’_x=f ‘_X(x,y)=

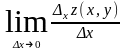
Аналогично частная производной функции Z по аргументу y:

Z’_y=f ‘_y(x,y)=

Правило 1. Чтобы найти частную производную функции нескольких аргументов по одному из них, нужно считать в выражении функции только этот аргумент переменной величины, а остальные - постоянными и пользоваться правилами и формулами дифференцирования функции одного аргумента.

Правило 2. Чтобы найти частный дифференциал функции нескольких аргументов по одному из них, надо умножить частную производную функции по этому аргументу на дифференциал этого аргумента:

частный дифференциал функции z=f(x,y) по аргументу x: d_xz=z'_x·dx

частный дифференциал функции z=f(x,y) по аргументу y: d_yz=z'_y·dy

Под дифференциалом независимой переменной понимается приращение этой переменной, т.е. dx=∆x dy=∆y.

Правило 3. Полный дифференциал функции нескольких аргументов равен сумме частных дифференциалов функции по всем ее аргументов.

Решение типовой задачи.

Задача: Найти полный дифференциал функции z=(3x²+5xy-7y³)⁵.

Решение. Функция z зависит от 2-х аргументов x и y, поэтому dz=d_xz+d_yz. Найдем сначала частные производные и частные дифференциалы функции z' _x=[(3x²+5xy-7y³)⁵]'x.

Используем формулу дифференцирования сложной степенной функции: (uⁿ)'_x=n·u^n-1·u'_x. В нашем примере n=5, u=3x²+5xy-7y³.

Получаем: z'_x=5(3x²+5xy-7y³)⁴·(3x²+5xy-7y³)'_x

Теперь применим правило 1 нахождения частной производной: будем считать в выражении 3x²+5xy-7y³ только x переменной, а y постоянной. Тогда (3x²+5xy-7y³)'_x= 6x+5y. В результате z'_x=5(3x²+5xy-7y³)⁴·(6x+5y).

Частный дифференциал функции z по аргументу x согласно правилу 2 имеет значение:

d_xz=5·(3x²+5xy-7y³)⁴·(6x+5y)dx

По тем же правилам находим Z'_y= 5(3x²+5xy-7y³)⁴·(3x²+5xy-7y³)'_y= = 5(3x²+5xy-7y³)⁴·(5x-21y²). D_yZ= 5(3x²+5xy-7y³)⁴·(5x-21y²)·dy

Складывая частные дифференциалы, находим полный дифференциал функции Z: dZ= 5(3x²+5xy-7y³)⁴·[(6x+5y)·dx+(5x-21y²)·dy].

5. Неопределенный интеграл

Определение 1. Первообразной функцией для данной функции f(x) на данном промежутке называется такая функция F(x), производная которой равна данной функции f(x) или дифференциал которой равен f(x)dx на рассматриваемом промежутке.

Определение 2. Совокупность первообразных F(x)+C для данной функции f(x) или данного дифференциала f(x)dx называется неопределенным интегралом от функции f(x) и обозначают ∫f(x)dx.

Вычисление интеграла от данной функции называют интегрированием этой функции.

Основные свойства неопределенного интеграла.

1⁰ Дифференциал неопределенного интеграла равен подынтегральному выражению, а производная от неопределенного интеграла равна подынтегральной функции: d∫f(x)dx=f(x)·dx; (∫f(x)dx)'=f(x).

2⁰ Неопределенный интеграл от дифференциала функции равен самой этой функции с точностью до постоянного слагаемого: ∫dF(x)=F(x)+C.

3⁰ Постоянный множитель можно выносить за знак неопределенного интеграла: ∫kf(x)dx=k∫f(x)dx.

4⁰ Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме неопределенных интегралов от этих функций:

∫[f₁(x)+f₂(x)-f₃(x)]dx=∫f₁(x)dx+∫f₂(x)dx-∫f₃(x)dx

Основные методы интегрирования.

1.Непосредственное интегрирование.

Этот способ основан на использовании свойств неопределенного интеграла и приведении подынтегрального выражения к табличной форме путем тождественных преобразований.

2. Интегрирование подстановкой (замена переменной).

Этот способ заключается в переходе от данной переменной интегрирования к другой переменной для упрощения подынтегрального выражения и приведения его к табличной форме.

В интеграле ∫f(x)dx заменим x=φ(t), dx= φ'(t)dt, тогда ∫f(x)dx=∫f(φ(t)· φ'(t)dt.

3.Интегрирование по частям.

При этом способе используют формулу ∫udv=uv-∫vdu (*)

К числу интегралов, вычисляемых по частям, относятся, например, интегралы вида ∫P(x)·f(x)dx, где P(x)- многочлен (в частности, степенная функция), а f(x)- одна из следующих функций: ex, sinax,

cosax, lnx, arcsinx, arccosx, arctgx, arcctgx. При этом для интегралов вида ∫P(x)·e^axdx, ∫P(x)sinaxdx, ∫P(x)cosaxdx, за U принимают многочлен P(x), а для интегралов вида ∫P(x)arcsinxdx, ∫P(x)arccosxdx, ∫P(x)arctgxdx, ∫P(x)arcctgxdx, ∫P(x)lnxdx за U принимается lnx, arcsinx, arccosx, arctgx, arcctgx.

Решение типовых задач.

Задача1. Решить методом непосредственного интегрирования

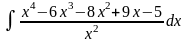
Решение. Сначала преобразуем подынтегральное выражение и получим ∫(x²-6x-8+ 9/x -5x^-2)dx.

Воспользуемся свойствами 4 и 3 неопределенного интеграла:

∫(x²-6x-8+ 9/x -5x^-2)dx=∫x²dx-6∫xdx-8∫dx+9∫dx/x -5∫x^-2dx

Все полученные интегралы табличные, поэтому, применяя формулы интегрирования, получаем:

Задача 2. Решить методом непосредственного интегрирования ∫tg²xdx.

Решение. Воспользуемся соотношением tg²x =1/cos²x -1 и преобразуем заданный интеграл:

Воспользуемся свойством 4 неопределенного интеграла и формулами интегрирования:

Задача 3. Решить методом подстановки ∫(x³+5)⁴·x²·dx

Решение. Заменим x³+5=t и продифференцируем это равенство: d(x³+5)=dt; 3x²·dx=dt. Сделаем замены в заданном интеграле:

∫(x³+5)⁴·x²·dx=

Возвращаясь к первоначальной переменой x, получаем: ∫(x³+5)⁴·x²dx = (x³+5)⁵/15 + C

Задача 4. Решить методом подстановки ∫sin⁷x cosx·dx.

Решение. Заменим в подынтегральном выражении sinx=t и продифференцируем это равенство: cosxdx=dt. Делаем замену в за­данном интеграле:

∫sin⁷x cosx dx = ∫t⁷·dt = t⁸/8 + C

∫sin⁷x cos x dx = sin⁸x/8 + C

Решение интеграла способом подстановки оформляют так:

∫sin⁷x cosx·dx= =∫t⁷·dt=

Задача 5. Решить методом интегрирования по частям ∫xlnxdx.

Решение. Согласно данным выше рекомендациям, заменим lnx=u, а ос­тавшееся выражение xdx=dv. Найдем du=d(lnx)=dx/x и функ­цию v из равенства dv=xdx. Тогда ∫dv=∫xdx, откуда v=x²/2 (полагаем С=0). Теперь, зная u=lnx, v=x²/2 и du=dx/x, применим формулу интегрирования по частям ∫udv = uv-∫vdu. В нашем примере имеем:

∫lnx·xdx=

∫xlnxdx=

Примечание: В некоторых случаях для приведения интеграла к табличному формулу интегрирования по частям применяют последовательно несколько раз.

Задача 6. Решить методом интегрирования по частям ∫x²·e^xdx

Решение: Согласно данным выше рекомендациям обозначим x²=u, а оставшееся выражение

е²dx=dv Найдем du=d(x²)=2xdx и функ­цию v из равенства dv=e^xdx, тогда ∫dv=∫e^xdx, откуда v=e^x.

Зная u=x², v=e^x и du=2xdx, применим формулу (*).

Получаем: ∫x²e^xdx=x·ex-2∫xe^xdx.

Полученный в правой части ∫xe^xdx проще данного, но не табличный. Поэтому решаем его, вновь применяя формулу (*). Обозначим x=u и dv=e^xdx. Найдем du=dx; v=∫e^xdx=e^x.

Решаем ∫xe^xdx=x·e^x-∫e^xdx=xe^x-e^x+c. Окончательно получаем: ∫x²e^xdx=x²·e^x-2(xe^x-e^x)+c=e^x(x²-2x+2)+c.

При решении интегралов по частям рекомендуется следующая форма записи: ∫x²e^xdx=x²·e^x-2∫xe^xdx=x²e^x-2(xe^x-∫e^xdx)=

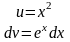
=x²e^x-2xe^x+2e^x+С = e^x(x²-2x+2)+С