
Билет №1. Понятие геометрического вектора. Основные определения, связанные с этим понятием (длина вектора, равенство векторов, нуль-вектор, коллинеарные и компланарные векторы, орт вектора). Линейные операции с геометрическими векторами. Законы, которым удовлетворяют эти операции. Разность векторов. Коллинеарные векторы.
Геометрический вектор – это направленный отрезок прямой, т. е. отрезок, один из концов которого является началом, а другой – концом.
Длина вектора АВ – это длина отрезка АВ. (Расстояние между началом и концом вектора называется его длиной или модулем). (обозначается модулем).
Равенство векторов. Векторы a и b равны, если они коллинеарные, одинаково направленные и имеют одинаковые длины. (2 вектора равны, если координаты, имеющие один и тот же номер, равны.)
Нуль-вектор – двухмерный вектор, координаты которого равны нулю. (Двухмерный вектор – упорядоченная пара чисел.) Вектор, у которого начало совпадает с концом.
Векторы a
и b
коллинеарные, если они лежат на одной
прямой или на параллельных прямых. Любые
два вектора
![]() и
и
![]() коллинеарны, если связаны соотношением
коллинеарны, если связаны соотношением
![]() ,
где
,
где
![]() - некоторое число.
- некоторое число.
Три вектора (или большее число) называются компланарными, если они, будучи приведенными к общему началу, лежат в одной плоскости.
Орт вектор – это единичный вектор, т. е. вектор, длина которого равна 1.
Линейные операции – это сложение и вычитание векторов, а также умножение вектора на число:
Сложение свободных векторов.
Суммой двух свободных векторов, таких, что начало вектора b приложено к вектору a, называется вектор с=a+b, который соединяет начало вектора a и конец вектора b.
Суммой двух свободных векторов, присоединенных к одному началу, называется вектор с, имеющий общее начало с векторами a и b и совпадают с диагональю параллелограмма, построенного на этих векторах.
Разность свободных векторов.
Умножение вектора на число. Произведением вектора на число называется вектор , определенный следующими условиями:
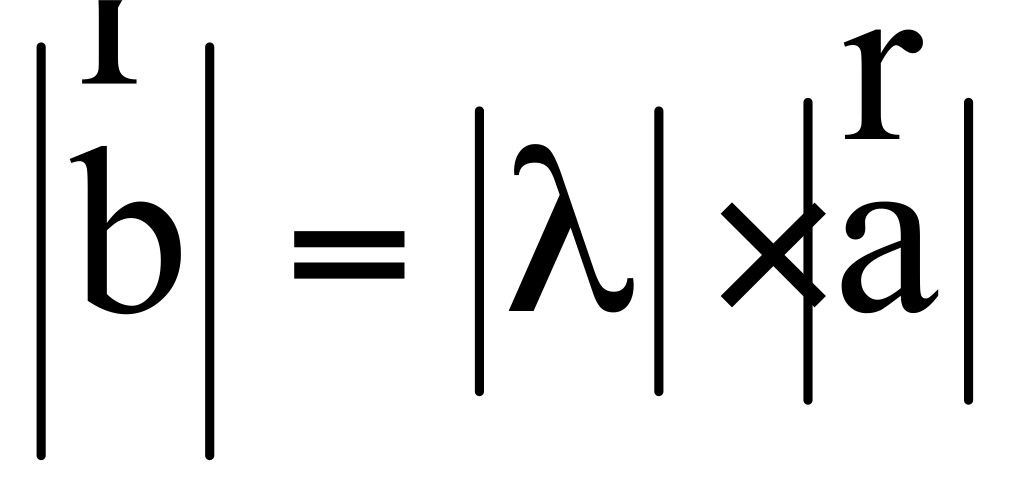
Вектор b коллинеарен вектору a
Векторы a и b одинаково направлены, если >0, и противоположно, если <0.
Разностью двух
векторов
и
называется такой вектор
![]() ,
сумма которого с вычитаемым
дает вектор
.
Значит, если
,
сумма которого с вычитаемым
дает вектор
.
Значит, если
![]() ,
то
,
то
![]() .
.
Свойства линейных операций:
+ = +
(a + b) + c = a + (b + c)
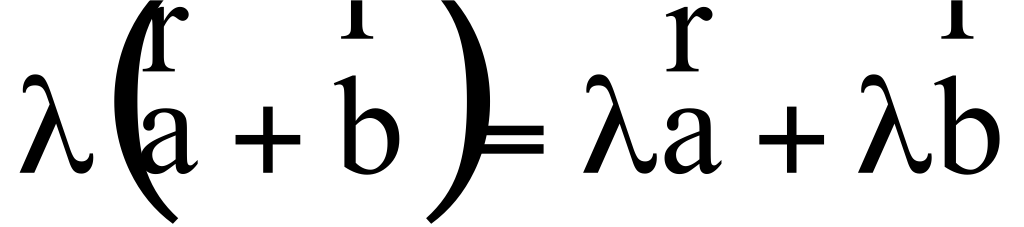
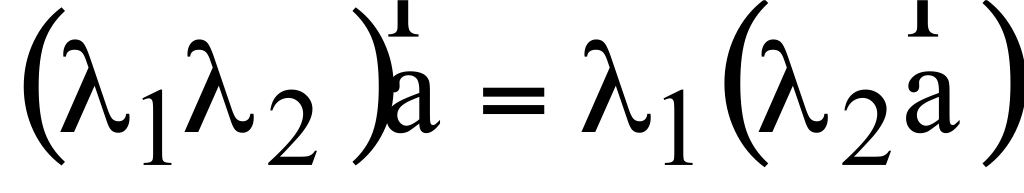

+ 0 =
+ (- ) = 0
1 * =
Билет №2. Декартова и полярная системы координат на плоскости. Формулы, связывающие координаты точки в этих системах. Декартова система координат в пространстве. Деление отрезка в заданном соотношении.
Декартовая система координат – прямоугольная система координат. Две взаимно перпендикулярные оси Ох и Оу, имеющие общее начало О и одинаковую масштабную единицу, образуют прямоугольную систему координат на плоскости.
Полярная система координат состоит из некоторой точки О, называемой полюсом, и исходящего из него луча ОЕ – полярной оси. Кроме того, задается единица масштаба для измерения длин отрезков. Полярная система координат ставит соответствие каждой точке плоскости пару чисел (Ро и фи) –> А (Ро; Фи).
Формулы, связывающие координаты точки в этих системах:
Пару полярных
координат r и
![]() можно перевести в Декартовы координаты
x и y путём применения тригонометрических
функций синуса и косинуса:
можно перевести в Декартовы координаты
x и y путём применения тригонометрических
функций синуса и косинуса:
x = rcos φ,
y = rsin φ,
в то время как две декартовы координаты x и y могут быть переведены в полярную координату r:
r2 = y2 + x2 (по теореме Пифагора).
Для определения угловой координаты следует принять во внимание два следующие соображения:
Для
![]() ,
может быть произвольным действительным
числом.
,
может быть произвольным действительным
числом.
Для
![]() , чтобы получить уникальное значение
, следует ограничиться интервалом в 2π.
Обычно выбирают интервал
, чтобы получить уникальное значение
, следует ограничиться интервалом в 2π.
Обычно выбирают интервал
![]() или
или
![]() .
.
Для вычисления в интервале , можно воспользоваться такими уравнениями (arctg обозначает обратную функцию к тангенсу):
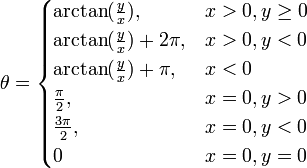
Для вычисления в интервале , можно воспользоваться такими уравнениями:
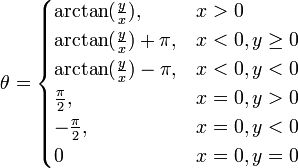
Прямоугольная (декартова) система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно одинаковы для всех осей (что не является обязательным). OX — ось абсцисс, OY — ось ординат, OZ — ось аппликат.
Деление отрезка в заданном соотношении.
Пусть на плоскости дан произвольный отрезок М1М2 и пусть М – любая точка этого отрезка, отличная от точки М2. Число , определяемое равенством:
= IM1MI/IMM2I,
Называется отношением, в котором точка М делит отрезок М1М2.
Билет №3. Понятие радиус-вектора. Разложение произвольного вектора по ортам координатных осей на плоскости и в пространстве. Действия с геометрическими векторами в координатной форме. Признак коллинеарности векторов.
Радиус-вектор – это вектор, начало которого совпадает с началом системы координат, а конец этого вектора с какой-либо точкой. (Особенность радиус-вектора – это то, что начало этого вектора всегда лежит в начале координат).
Разложение произвольного вектора по ортам координатных осей в пространстве (на плоскости аналагично):
Рассмотрим в пространстве прямоугольную систему координат Oxyz. Выделим на координатных осях Ох, Оу и Oz единичные векторы (орты), обозначаемые i , j , k соответственно:
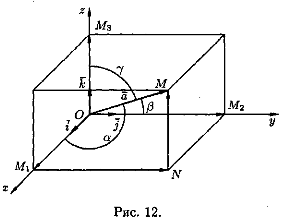
Выберем произвольный вектор а пространства и совместим его начало с началом координат: а=ОМ.
Найдем проекции вектора а на координатные оси. Проведем через конец вектора ОМ плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с осями обозначим соответственно через М1 , М2 и Мз. Получим прямоугольный параллелепипед, одной из диагоналей которого является вектор ОМ. Тогда пр ха=|OM 1|, npya = |ОМ2|, прz а=|ОМз|. По определению суммы нескольких векторов находим а = ОМ 1 + M1N + NM.
А так как M 1N=OM 2 , NM =ОМз, то
а=ОМ 1 + ОМ 2 + ОМ3 (5.1)
![]()
Обозначим проекции вектора а=ОМ на оси Ох, Оу и Oz соответственно через ах, ау и az, т.е. |OM 1| = ах,|ОМ2| = ау, |ОМ3| = аz. Тогда из равенств (5.1) и (5.2) получаем
a=axi+ayj+azk (5.3)
Эта формула является основной в векторном исчислении и называется разложением вектора по ортам координатных осей. Числа ах, ау, az называются координатами вектора а, т. е. координаты вектора есть его проекции на соответствующие координатные оси.
Признак коллинеарности векторов:
Для коллинеарности
вектора
![]() ненулевому вектору
ненулевому вектору
![]() необходимо и достаточно, чтобы
существовало такое число λ, что
необходимо и достаточно, чтобы
существовало такое число λ, что
![]()
Билет № 4. Скалярное произведение геометрических векторов и его свойства. Вычисление скалярного произведения векторов через их координаты, длина вектора, расстояние между двумя точками, вычисление косинуса угла между двумя векторами.
Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.
Скалярное произведение 2ух векторов a и b обозначается символом ab (порядок записи множителей безразличен, т. е. ab=ba)
Если угол между
векторами a
и b
обозначить
![]() ,
то их скалярное произведение можно
выразить формулой
,
то их скалярное произведение можно
выразить формулой
![]() .
.
Скалярное произведение aa называется скалярным квадратом вектора и обозначается символом a2.
Свойства скалярного произведения векторов:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Скалярное произведение в координатах:
Если![]()
![]() то
то![]()
![]()
Вычисление косинуса угла между двумя векторами:
![]()
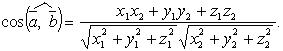
Расстояние между двумя точками:
Для любых двух точек М1 (х1;у1) и М2 (х2;у2) плоскости расстояние d между ними выражается формулой:
![]()
Длина вектора:
Длина вектора – это расстояние между началом и концом вектора – модуль вектора.
Для нахождения длины вектора используется следующая формула:
![]() ,
где
- координаты вектора.
,
где
- координаты вектора.
Билет №5. Общее уравнение прямой на плоскости и егое исследование. Уравнение прямой с угловым коэффициентом. Геометрический смысл коэффициентов. Пучок прямых. Уравнение прямой, проходящей через две заданные точки на плоскости и в пространстве. Условия параллельности и перпендикулярности прямых на плоскости.
Рассмотрим уравнение прямой с угловым коэффициентом
 .
Перенесем все слагаемые в левую часть
и перепишем его в следующем виде:
.
Перенесем все слагаемые в левую часть
и перепишем его в следующем виде:

(3.6)
![]() - общее уравнение прямой, где А и В не
равны нулю одновременно, т.е.
- общее уравнение прямой, где А и В не
равны нулю одновременно, т.е.
![]() .
.
Рассмотрим частные случаи уравнения (3.6):
Пусть
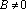 .
Тогда уравнение
можно записать в виде:
.
Тогда уравнение
можно записать в виде:
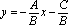 .
Обозначим
.
Обозначим
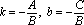 .
.
Если
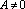 ,
,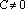 ,
то получим
,
то получим
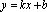 (уравнение прямой с угловым коэффициентом);
(уравнение прямой с угловым коэффициентом);Если ,
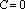 , то
, то
 (уравнение прямой, проходящей через
начало координат);
(уравнение прямой, проходящей через
начало координат);Если
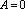 ,
, то
,
, то
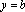 (уравнение прямой, параллельной оси
Оу);
(уравнение прямой, параллельной оси
Оу);Если , , то
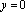 (уравнение оси Ох).
(уравнение оси Ох).Пусть
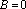 ,
.
Тогда уравнение
примет вид
,
.
Тогда уравнение
примет вид
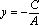 .
Обозначим
.
Обозначим
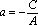 .
.Если , то получим х=а (уравнение прямой, параллельной оси Оу);
Если , то
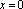 (уравнение оси Оу).
(уравнение оси Оу).
Таким образом, при любых значениях коэффициентов А,В (не равных одновременно нулю) и С уравнение есть уравнение некоторой прямой линии на плоскости Оху.
Уравнение прямой с угловым коэффициентом.
y = kx + b, (1)
где k - угловой коэффициент прямой, т. е. тангенс того угла, который прямая образует с положительным направлением оси Ox, причем этот угол отсчитывается от оси Ox к прямой против часовой стрелки, b - величина отрезка, отсекаемого прямой на оси ординат. При b = 0 уравнение (1) имеет вид y = kx и соответствующая ему прямая проходит через начало координат.
Геометрический смысл коэффициентов:
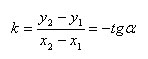
Коэффициент k (угловой коэффициент) в уравнении прямой с точностью до знака равен тангенсу острого угла, который образует прямая с осью x.
Пучок прямых.
Совокупность прямых, проходящих через некоторую точку S, называется пучком прямых с центром в S.
Если
![]() и
и
![]() - уравнения двух прямых, пересекающихся
в точке S, то уравнение
- уравнения двух прямых, пересекающихся
в точке S, то уравнение
![]() ,
(1)
,
(1)
Где
![]() ,
,
![]() - любые числа, не равные одновременно
нулю, определяет прямую, также проходящую
через точку S.
- любые числа, не равные одновременно
нулю, определяет прямую, также проходящую
через точку S.
Более того, в уравнении (1) числа , всегда возможно подобрать так, чтобы оно определило любую (заранее назначенную) прямую, проходящую через точку S, иначе говоря, любую прямую пучка с центром S. Поэтому уравнение вида (1) называется уравнением пучка (с центром в S).
Если
![]() ,
то, деля обе части уравнения (1) на
и полагая
,
то, деля обе части уравнения (1) на
и полагая
![]() ,
получим
,
получим
![]() .
(2)
.
(2)
Этим уравнением
можно определить любую прямую пучка с
центром S, кроме той, которая соответствует
![]() ,
то есть кроме прямой
.
,
то есть кроме прямой
.
Условие параллельности и перпендикулярности прямых:
Равенство коэффициентов является необходимым и достаточным условием параллельности прямых. (к1=к2=кn).
Для перпендикулярности
прямых необходимо и достаточно, чтобы
их угловые коэффициенты были обратны
по величине и противоположны по знаку.
(![]() ).
).
Уравнение прямой, проходящей через две заданные точки на плоскости и в пространстве.
Пусть в пространстве заданы две точки M1(x1, y1, z1) и M2(x2, y2, z2), тогда уравнение прямой, проходящей через эти точки:
![]()
Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.
На плоскости записанное выше уравнение прямой упрощается:
![]()
Дробь
![]() = k называется угловым коэффициентом
прямой.
= k называется угловым коэффициентом
прямой.
Билет №6. Общее уравнение плоскости и его исследование. Различные виды уравнений прямой в пространстве (каноническое, параметрическое, общее уравнение прямой).
Рассмотрим общее уравнение первой степени с тремя переменными х, у и z:
![]() (12.4)
(12.4)
Полагая, что по
крайней мере один из коэффициентов А,
В или С не равен нулю, например
![]() ,
перепишем уравнение (12.4) в виде:
,
перепишем уравнение (12.4) в виде:
![]() (12.5)
(12.5)
Сравнивая уравнение
(12.5) с уравнением (12.3), видим, что уравнения
(12.4) и (12.5) являются уравнением плоскости
с нормальным вектором
![]() ,
проходящей через точку
,
проходящей через точку
![]()
Итак, уравнение (12.4) определяет в системе координат Oxyz некоторую плоскость. Уравнение (12.4) называется общим уравнением плоскости.
Частные случаи общего уравнения плоскости:
1. Если D = 0, то оно
принимает вид
![]() .
Этому уравнению удовлетворяет точка
.
Этому уравнению удовлетворяет точка
![]() .
Следовательно, в этом случае плоскость
проходит через начало координат.
.
Следовательно, в этом случае плоскость
проходит через начало координат.
2. Если С = 0, то
имеем уравнение
![]() .
Нормальный вектор
.
Нормальный вектор
![]() перпендикулярен оси Οz. Следовательно,
плоскость параллельна оси Οz; если B = 0
— параллельна оси Оу, А = 0 — параллельна
оси Ох.
перпендикулярен оси Οz. Следовательно,
плоскость параллельна оси Οz; если B = 0
— параллельна оси Оу, А = 0 — параллельна
оси Ох.
3. Если С = D = 0, то
плоскость проходит через
параллельно оси Οz, т. е. плоскость
![]() проходит через ось Οz. Аналогично,
уравнениям
проходит через ось Οz. Аналогично,
уравнениям
![]() и
и
![]() отвечают плоскости, проходящие
соответственно через оси Ох и Оу.
отвечают плоскости, проходящие
соответственно через оси Ох и Оу.
4. Если А = В = 0, то
уравнение (12.4) принимает вид
![]() ,
т. е.
,
т. е.
![]() Плоскость параллельна плоскости Оху.
Аналогично, уравнениям
Плоскость параллельна плоскости Оху.
Аналогично, уравнениям
![]() и
и
![]() отвечают плоскости, соответственно
параллельные плоскостям Oyz и Οxz.
отвечают плоскости, соответственно
параллельные плоскостям Oyz и Οxz.
5. Если A = B = D = 0, то
уравнение (12.4) примет вид
![]() ,
т. е. z = 0. Это уравнение плоскости Оху.
Аналогично: у = 0 — уравнение плоскости
Οxz; x = О — уравнение плоскости Oyz.
,
т. е. z = 0. Это уравнение плоскости Оху.
Аналогично: у = 0 — уравнение плоскости
Οxz; x = О — уравнение плоскости Oyz.
Виды уравнений:
Каноническое и параметрическое уравнения:
Если известна одна
точка
![]() прямой и направляющий вектор
прямой и направляющий вектор
![]() ,
то прямая может быть определена (двумя)
уравнениями вида
,
то прямая может быть определена (двумя)
уравнениями вида
![]() .
(1)
.
(1)
В таком виде уравнения прямой называются каноническими.
Канонические
уравнения прямой, проходящей через
данные точки
![]() и
и
![]() имеют вид
имеют вид
![]() .
(2)
.
(2)
Обозначим буквой t каждое из равных отношений в канонических уравнениях (1); получим:
![]() .
.
Отсюда:
![]() ,
,
![]() ,
,
![]() (3)
(3)
Это - параметрические
уравнения прямой, проходящей через
точку
![]() в направлении вектора
.
В уравнениях (3) t рассматривается как
произвольно изменяющийся параметр, x,
y, z - как функции от t; при изменении t
величины x, y, z меняются так, что точка
M(x; y; z) движется по данной прямой.
в направлении вектора
.
В уравнениях (3) t рассматривается как
произвольно изменяющийся параметр, x,
y, z - как функции от t; при изменении t
величины x, y, z меняются так, что точка
M(x; y; z) движется по данной прямой.
Общее уравнение прямой (см. билет 5)
Билет №7. Окружность и ее уравнение. Определение эллипса и его каноническое уравнение.
Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая.Уравнение окружности ω (A; R) имеет вид (x – a)2 + (y – b)2 = R2, где a и b – координаты центра A окружности ω (A; R) .
Доказательство:
Пусть задана окружность ω (A; R) на плоскости Oxy, где точка A, центр окружности – имеет координаты a и b. По определению окружности для любой точки B (x; y), лежащей на окружности ω (A; R), верно AB = R. Но в соответствии с теоремой (Если A1 (x1; y1), A2 (x2; y2) две произвольные точки плоскости Oxy, а d – расстояние между ними, то d вычисляется из соотношения d2 = (x1 – x2)2 + (y1 – y2)2)AB2 = (x – a)2 + (y – b)2. Таким образом, координаты x и y любой точки окружности ω (A; R) удовлетворяют уравнению (x – a)2 + (y – b)2 = R2.
Обратно: любая точка B (x; y), координаты которой удовлетворяют уравнению, принадлежит окружности, так как расстояние от нее до точки A (a; b) равно R. Отсюда по определению данное уравнение – уравнение окружности ω (A; R).
Эллипс – множество всех точек плоскости, для которых сумма расстояний от двух данных точек, называемых фокусом, есть величина постоянная, большая, чем расстояние между фокусами.
Пусть сумма расстояний от точки эллипса до фокусов равна 2а, а расстояние между фокусами – 2с. Тогда в выбранной системе координат эллипс имеет уравнение (каноническое уравнение):
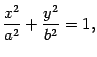
Где
![]()
Билет №8. Определение гиперболы и ее каноническое уравнение.
Гипербола – это множество всех точек на плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.
Пусть расстояние между фокусами F1 и F2 гиперболы равно 2c, а абсолютная величина разности расстояний от точки гиперболы до фокусов равна 2a. Тогда гипербола в выбранной выше системе координат имеет уравнение (каноническое уравнение):
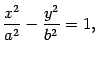
Где
![]()
Билет №9. Матрицы и основные определения, связанные с этим понятием (квадратная матрица, прямоугольная матрица, треугольная матрица, трапецеидальная матрица, диагональная матрица, единичная матрица, нулевая матрица, транспонированная матрица, скалярная матрица). Действия с матрицами (сложение, умножение на скаляр, перемножение матриц, транспонирование матриц). Законы, которым эти действия удовлетворяют.
Матрица (mxn) – прямоугольная таблица чисел, в каждой клетке которой находится число, однозначно определяемое его местоположение. (Матрицей называется прямоугольная таблица из чисел, содержащая некоторое количество m строк и некоторое количество n столбцов.)
Квадратная матрица – это матрица, которая имеет одинаковое количество строк и стольцов, т.е. m=n.
Прямоугольная матрица – это ОБЫЧНАЯ МАТРИЦА!!!!!!!! (НЕ НАШЛА НИГДЕ ОПРЕДЕЛЕНИЯ!)
Треугольная матрица – Квадратная матрица, все элементы которой выше или ниже главной диагонали равны нулю. (2 вида треугольной матрицы: верхняя треугольная и нижняя треугольная).
Трапецеидальная (ступенчатая) матрица – прямоугольная матрица, которую можно разделить вертикальной чертой так, что слева получится треугольная матрица, а справа – прямоугольная.
Диагональная (скалярная матрица) – матрица, все элементы которой, кроме элементов главной диагонали, равны нулю.
Единичная матрица – это матрица, элементы главной диагонали которой равны 1, а все остальные – нулю.
Нулевая матрица – матрица, все элементы которой равны нулю.
Матрица А является транспонированной по отношению к матрице В, если столбцы матрицы А являются строками матрицы В.
Действия с матрицами:
Сложение:
Суммой двух матриц одинакового размера называется матрица такого же размера, каждый элемент которой равен сумме соответствующих элементов слагаемых.
A + B = C <=> cij=aij + bij
Свойства сложения:
А + В = В + А
(А + В) + С = А + (В + С)
А + 0 = А
А + (-А) = 0
Разность:
Разностью двух матриц одинакового размера называется матрица того же размера, каждый элемент которой равен разности соответствующих элементов данных матриц.
А – В = А + (-В) = С <=> cij=aij - bij
Умножение матрицы на скаляр:
Произведением матрицы на число называется матрица того же размера, каждый элемент которой равен произведению соответствующего элемента данной матрицы на это число.
а*В=С <=> cij=a*bij
Свойства:
1 * А = А, (-1) * А = -А
a*(bA)=(ab)A
a(A+B)=aA+aB
(a+b)A=aA+bA
Умножение матриц.
Умножением матрицы размера mXn на матрицу размера nxk называется матрица размера mxk, элементы которой, стоящие на пересечении i-ой строки и j-ого столбца, равен сумме произведений соответствующих элементов i-ой строки на элементы j-ого столбца.
Свойства:
AE = EA = A
A = 0a = 0
(AB)C = A(BC)
a(AB) = (aA)B = A(aB)
(A+B)C = AC + BC
C (A + B) + CA + CB
A0=E; A1=A; при k>1 Ak = A * Ak-1 = Ak-1 * A/
Если А и В – квадратные матрицы одного и того же порядка, причем AB=BA, то
(A+B)2=A2+2AB+B2
(A-B)2=A2-2AB+B2
(A-B)(A+B) = A2-B2
Транспонирование матриц:
Транспонированной по отношению к матрице А называется матрица АТ, столбцы которой являются строками матрицы А с теми же номерами.
Билет №10. Определения определителя и его свойства. Определитель, минор и алгебраическое дополнение элемента определителя. Вычисление определителя произвольного порядка.
Определитель матрицы – это число, которое сопоставляется квадратной матрице по определенному закону. (обозначается II либо det)
Свойства:
Det (AB) = det A * det B
Det A = det AТ
Det A-1=1/detA
Если все элементы какой-либо строки или столбца определителя равны нулю, то определитель тоже равен нулю.
Если матрица В получена из матрица А перестановкой каких-либо 2ух строк или столбцов, то debt = -detA.
Общий множитель всех элементов любой строки или столбца можно выносить за знак определителя.
Определитель, содержащий 2 пропорциональные строки или столбца, равен нулю.
Определитель не меняется от прибавления к какой-либо строке (столбцу) другой строки (столбца), умноженной(ого) на произвольное число.
Если какая-либо строка (столбец) есть линейная комбинация другой строки (столбца), то такой определитель равен нулю.
Минором (Mij) называется определитель, полученный из исходной матрицы вычеркиванием строки и столбца на пересечении которых стоит элемент aij.
Алгебраическим дополнением элемента aij матрицы А называется минор, умноженный на (-1)i+j
Определителем матрицы второго порядка называется число, равное разности между произведением элементов главной диагонали и произведением элементов побочной диагонали.
Определитель матрицы n-ого порядка вычисляется путем разложения строки или столбца.
Билет №11. Обратная матрица. Способы вычисления обратной матрицы.
Матрица А является обратной матрицей матрице В, если выполняется равенство: АВ=ВА=Е. Из определения следует, что В будет квадратной матрицей того же порядка что и матрица А (иначе одно из произведений АВ или ВА было бы не определено).
Существую несколько способов нахождения обратной матрицы. Один из них – нахождение обратной матрицы путём вычисления алгебраических дополнений. Заключается он в следующем:
пусть нам дана матрица А, имеющая следующий вид:
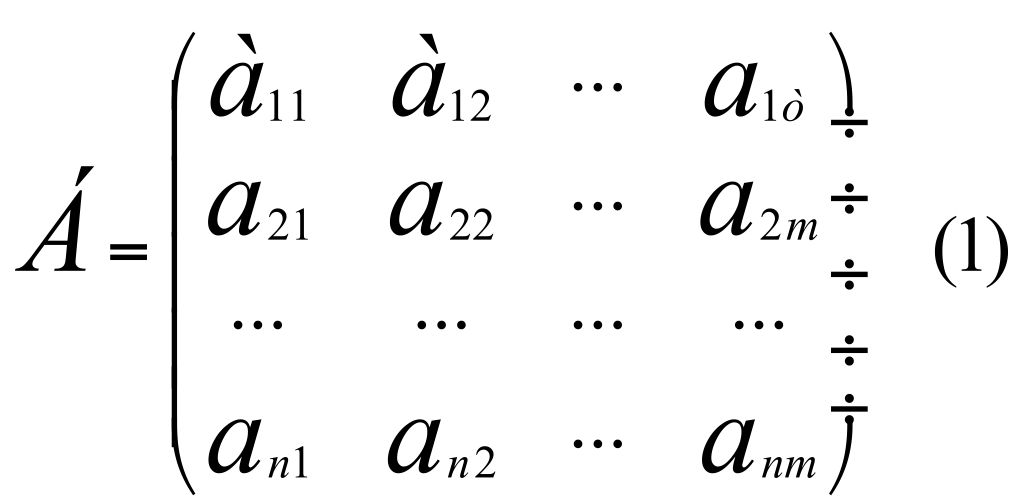
Предположим, что ΔА≠0. Построим следующую матрицу С следующим образом:
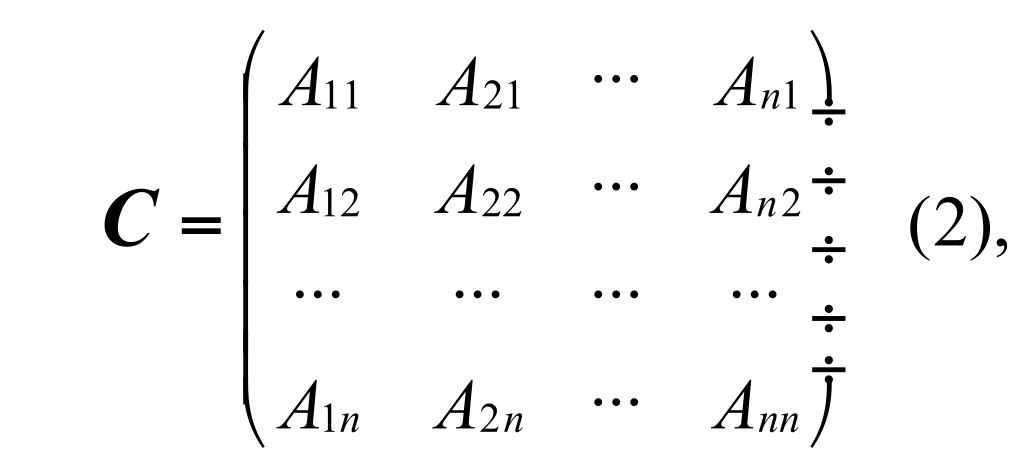
где Аij – алгебраическое дополнение элемента аij в определителе матрицы А. Очевидно, что для построения матрицы С необходимо сначала заменить элементы матрицы А соответствующими им алгебраическими дополнениями, а затем полученную матрицу транспонировать.
Полученная таким образом матрица С называется присоединённой к матрице А, или союзной с А.
Чтобы получить матрицу А-1, обратную для матрицы А, необходимо каждый элемент присоединённой матрицы С поделить на ΔА, т.е. матрица А-1 будет иметь следующий вид:
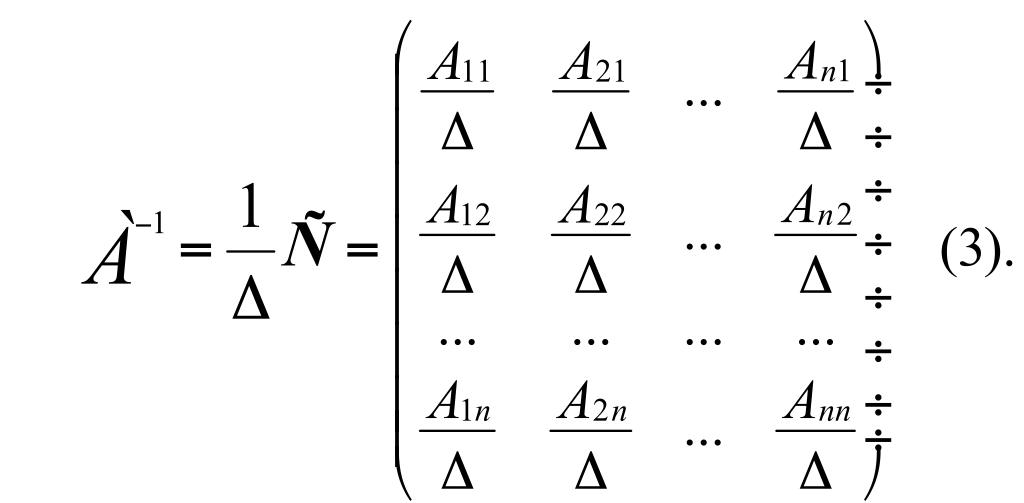
Пусть матрица А, имеет следующий вид:
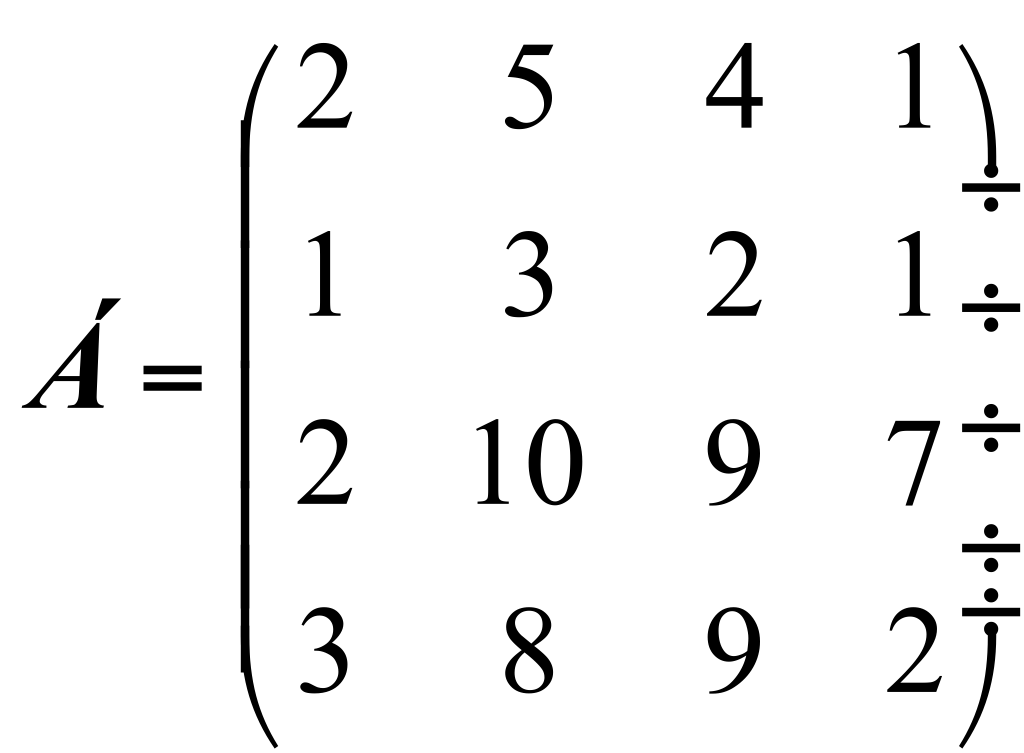
Чтобы найти матрицу А-1, обратную для матрицы А, необходимо:
вычислить определитель матрицы (ΔА= -3);
найти алгебраические дополнения элементов аij в определителе матрицы А:

составить присоединённую матрицу С по формуле (2);
разделить все элементы матрицы С на ΔА.
