12. Евклидово точечное пространство. Прямоугольная система координат.

Евклидово пространство получается из n-мерного действительного линейного пространства путем введения в него скалярного произведения. Пусть задано n-мерное действительное аффинное пространство , связанное с действительным линейным пространством . Задавая на скалярное произведение, т.е.превращая его в пространство , мы преобразуем аффинное пространство в евклидово точечное пространство . Итак, имеет место следующее

Определение 26.1. Аффинное пространство, связанное с евклидовым пространством , называется n-мерным евклидовым точечным пространством и обозначается .

В n-мерном пространстве можно ввести ряд понятий, обобщающих известные понятия в трехмерном пространстве .

Определение 26.2. Репер (1) пространства в случае ортонормированного базиса 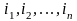(2) будем называть прямоугольной системой координат, а координаты точек и векторов относительно такого репера – прямоугольными.

Так как в любом ненулевом n-мерном евклидовом пространстве существуют ортонормированные базисы (см. § 23.6), то в любом евклидовом точечном пространстве ,n , существуют прямоугольные системы координат.

Пусть в пространстве заданы две прямоугольные системы координат: (1) и (3)

Если -координаты точки М в репере (1), - координаты этой же точки в репере (3), ,- координаты точки О` в репере (1) и А= - матрица перехода от базиса (2) к базису (4)

то, как показано в § 25.2, старые координаты точки М связаны с новыми координатами этой точки формулами:

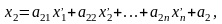
………………………………….. (5)

Использовав обозначения (8) из § 25.2, можно записать эти формулы в матричном виде: X=A (6)

Так как базисы (2) и (4) – ортонормированные, то матрица А в формуле (6) – ортогональная.

Определение 26.3. Расстоянием между точками М и N пространства называется длина вектора .

Итак, обозначая указанное расстояние через , имеем =

Если заданы прямоугольные координаты точек М и N: М ( ), N( ), то =

13. Плоскости евклидова точечного пространства.

Так как пространство удовлетворяет аксиомам аффинного пространства (см. определение 25.1), то в существуют плоскости любой размерности k, где 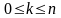, причем нуль-мерные плоскости – это точки, а единственная n-мерная плоскость совпадает с пространством . Очевидно, что всякая плоскость пространства является k-мерным евклидовым точечным пространством.

Возьмем в пространстве две одномерные плоскости, т.е. прямые ∆, ,. Пусть а- какой-либо направляющий вектор прямой и -направляющий вектор прямой .

Определение 26.4. Углом между прямыми ∆ и называется угол между их направляющими векторами а, , т.е. число , определяемое формулой cos ,

Заметим, что угол между прямыми и не зависит от выбора направляющих векторов этих прямых.

Пусть в пространстве заданы две плоскости – плоскость с начальной точкой М и направляющим пространством и плоскость с начальной точкой N и направляющим пространством .

Определение 26.5. Плоскости и называются ортогональными, если они имеют общую точку и каждый вектор из пространства ортогонален каждому вектору из пространства .

Лемма 10. Если плоскости и ортогональные, то они имеют только одну общую точку. Док-во: Пусть М`, N`-две различные точки, принадлежащие и плоскости , и плоскости . Тогда вектор принадлежит и пространству , и прострнству , поэтому · =0. Но это невозможно, так как .

Определение 26.6. Ортогональным дополнением плоскости пространства называется (n-k)-мерная плоскость, ортогональная плоскости .

Теорема 26.1. Если в пространстве задана плоскость , то через каждую точку N пространства проходит единственное ортогональное дополнение этой плоскости.

Док-во: Пусть плоскость задана начальной точкой М и направляющим пространством . Рассмотрим ортогональное дополнение ( ) подпространства в пространстве . Пусть 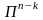- плоскость в пространстве с начальной точкой N и направляющим пространством ( ). Так как , то согласно теореме 25.7, плоскости и имеют общую точку. Итак, - искомое ортогональное дополнение плоскости .

Единственность ортогонального дополнения плоскости следует из того, что каждая плоскость однозначно определяется заданием какой-либо ее точки и направляющего пространства.

Рассмотрим (n-1)-мерную плоскость, т.е. гиперплоскость и прямоугольную систему координат

(O, ). (1)

Пусть ( ) - некоторая точка гиперплоскости и - направляющее пространство для . Согласно теореме 26.1, через точку проходит одномерное ортогональное дополнение плоскости , т.е. прямая ∆ . Пусть n( )- какой-либо направляющий вектор прямой ∆ и М ( )- произвольная точка пространства . Точка М принадлежит плоскости тогда и только тогда, когда векторы n и ортогональны, т.е. =0. Записывая это равенство в координатах, получаем (2)

Этому уравнению относительно удовлетворяют координаты любой точки плоскости , и только такой точки. Другими словами, уравнение (2) является уравнением плоскости . Отметим, что эта плоскость проходит через точку ( ) и ортогональна вектору n( ), т.е. прямой с направляющим вектором n. Запишем уравнение (2) гиперплоскости в виде (3)

Пусть N( ) - произвольная точка пространства .Рассмотрим прямую , проходящую через точку N и являющуюся ортогональным дополнением гиперплоскости . Эта прямая пересекает гиперплоскость в некоторой точке Р( ).