Электростатика.
Электростатика
изучает неподвижные электрические
заряды.
Заряд электрона:
Кл =
ед. cyst
зар.
Масса электрона:
кг. Радиус электрона:
см.
Заряд протона:
Кл. Масса протона:
кг.
Радиус протона:
см.
З
;
;
;
;
;
– Абсолютная диэлектрическая проницаемость вакуума.
– Сила взаимодействия зарядов.
или
.
,
при
кл,
м,
;
1 дн = 1 (г·см)/с2 ; 1 Н ((кг·м)/с2) = 105 дн.
Точечный заряд – это заряженное тело, размерами которого можно пренебречь.
;
– объёмная плотность заряда.
.
– поверхностная
плотность заряда.
.
– линейная
плотность заряда.
.
Напряжённость электрического поля.
Пространство, окружающее электрический заряд – электрическое поле.
– заряд;
– пробный заряд.
,
.
– сила,
действующая на пробный заряд в этой
точке – напряжённость.
Напряжённость
– сила,
действующая на пробный заряд. Это силовая
характеристика.
.
Принцип суперпозиции.
;
.
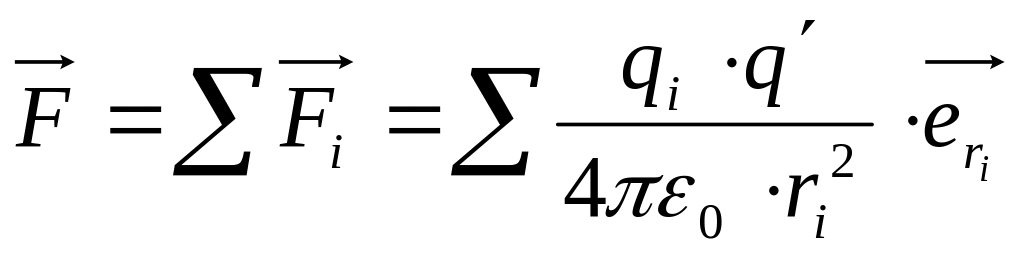Напряжённость электрического поля протяжённых макроскопических тел.
.
Для
объёмного тела:
.
Для
плоскости:
.
Для
кривой линии:
.
Электрические силовые линии.
Электрическое
поле –
материальная среда, неоднородность,
возникающая в физическом вакууме. Из-за
этих неоднородностей и возникают
электрические силы. Силовые
линии –
направление сил, действующих на пробный
заряд.
Поток напряжённости электрического поля.
Потоком
напряжённости электрического поля
через площадку называется число силовых
линий, прошедших через площадку.
.
.
.
Задача:
Кольцо
;
;
– ? в точке на оси z.
.
Проекции на оси
и
компенсируют друг друга. Остаётся только
проекция на ось
:
.
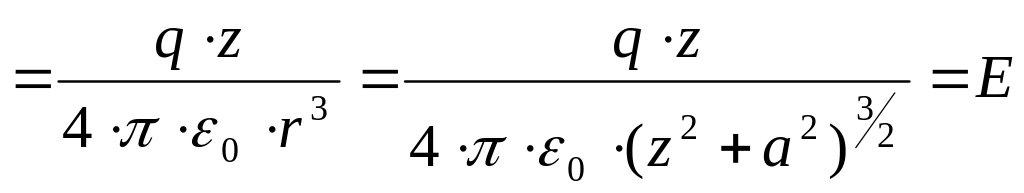– кольцо.
При
:
,
то есть кольцо ведёт себя как точечный
заряд.
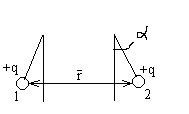
Задача:
Найти силу взаимодействия
нити и кольца (нить проходит через
кольцо).
.
.
.
.
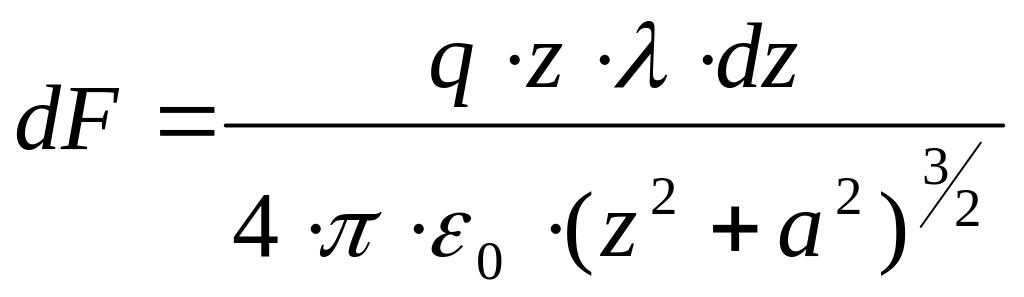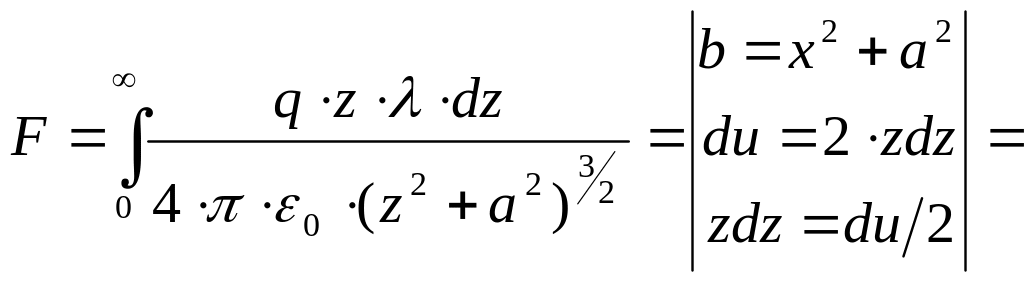
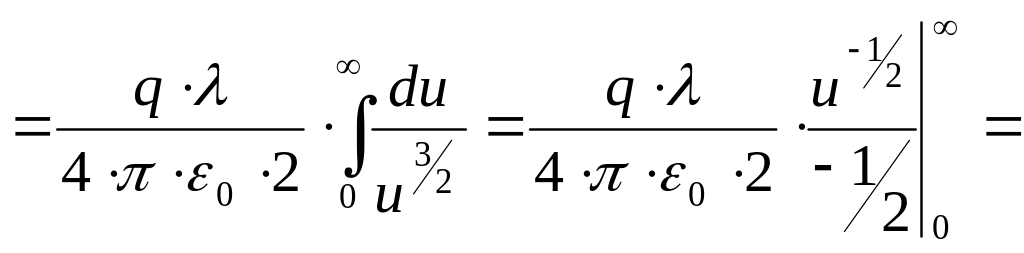
Задача:
стержень
длиной
,
имеет заряд
.
Найти
.
–
расстояние до стержня.
.
.
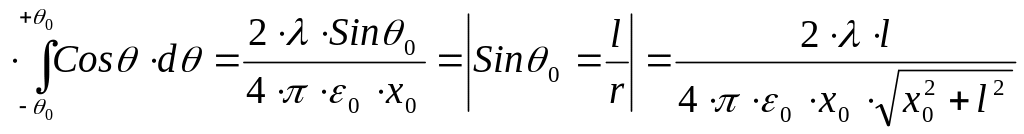Индукция электрического поля.
Обозначается
.
В вакууме
.
Вектор индукции касателен силовым
линиям.
– поток
вектора
через поверхность
.
Тензоры электрического поля.
Скалярное
поле – каждой
точке пространства определяется
конкретное число. Векторное
поле – каждой
точке пространства определяется три
числа (три компонента), что задаёт
направление.
;
;
;
.
Поле
тензоров второго ранга:
,
(9 компонентов).
Поле
тензоров третьего ранга:
,
.
(27 компонентов).
Тензор
-го
ранга имеет
компонентов. Скаляр и вектор тоже
тензоры.
Дифференцирование тензоров электрического поля.
– оператор
набла.
.
.
.
.
Примеры:
;
.
;
.
Дифференцирование векторных полей.
– дивергенция.
(ротор)
.
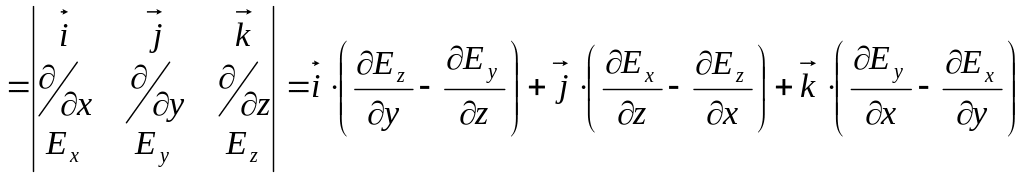Теорема Гаусса в электростатике.
– поле.
S
– замкнутая поверхность.
– полный поток векторного поля через
любую замкнутую поверхность. Например:
.
.
– полный поток
через сферическую поверхность.
Теорема Гаусса в интегральном виде.
Если
заряд распределён внутри поверхности,
то
,
и
.
.
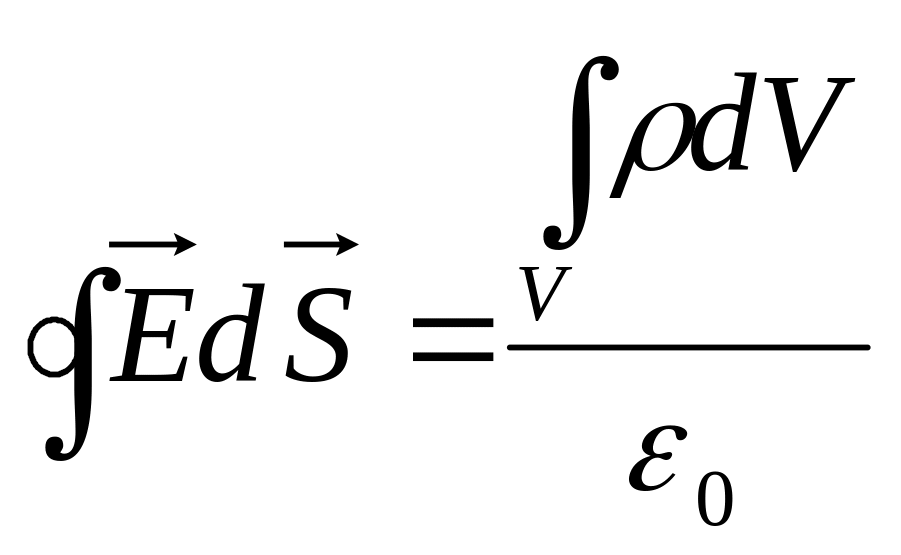– теорема Гаусса в дифференциальном
виде.
=>
.
– теорема Гаусса для индукции, где
.
;
;
.
– теорема
Гаусса для индукции в дифференциальном
виде.
Металлы в электростатике.
В
металлах есть свободные электрические
заряды; в диэлектриках все электрические
заряды связаны между собой. Внутри
металла всегда Е = 0 в результате
поляризации (заряды выстраиваются в
определённом порядке).
– тангенциальная составляющая на
поверхности металла; так как заряд не
двигается.
–площадь
поперечного сечения цилиндра,
.
– площадь цилиндра.
;
;
;
;
,
.
.
.
Задача:
заряженная плоскость. Найти
и
в т. А. Возьмём цилиндр и точка А будет
лежать на основании этого цилиндра. S
– площадь основания цилиндра.
.
Для боковой поверхности цилиндра
,
так как
,
,
но из-за симметрии
,
и поэтому
– для любой точки независимо от расстояния
от плоскости.
.
Задача:
дана сфера:
,
и
– полный заряд. Найти
и
в произвольной точке на расстоянии
от центра сферы.
:
.
,
– сфера действует как точечный заряд.
:
– внутри заряженной сферы.
Задача: даны 3 сферы.
:
;
:
;
:
;
:
.
Задача:
найти
заряженной нити на расстоянии
.
Строим цилиндр и точка А будет находится
на его боковой стороне.
.
Индукция и напряжённость остаются
только от боковой стороны, так как на
основаниях они
.
;
,
.
Задача:
найти
и
заряженного цилиндра
длины:
и
.
: – внутри цилиндра поля нет;
:
;
,
– как для
нити.
Задача:
найти
и
на расстоянии
от заряженного шара:
,
.
:
,
,
.
:
,
.
Конденсатор.
Плоский:
вне конденсатора электрическое поле
равно нулю (компенсируется двумя
пластинами). Внутри конденсатора:
,
.
Ц
.
При
,
Работа электрического поля. Потенциал.
,
.
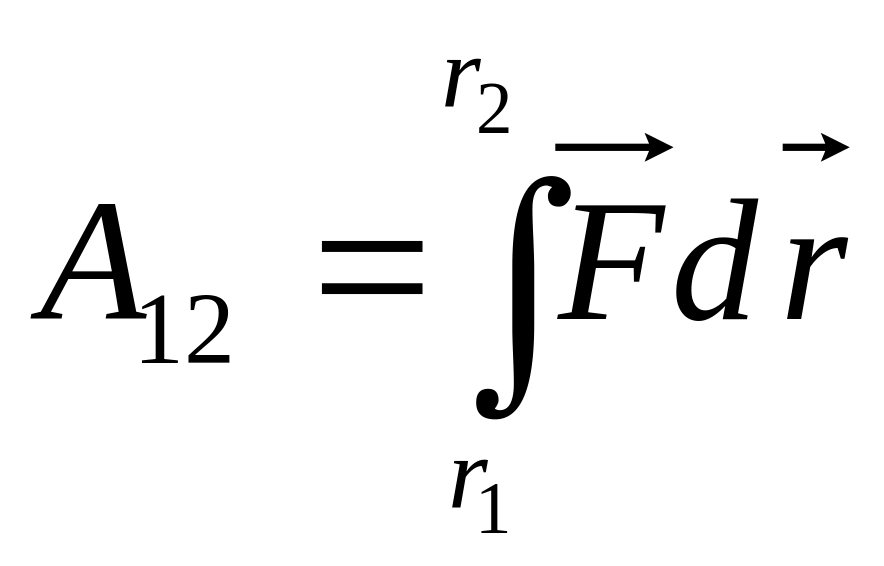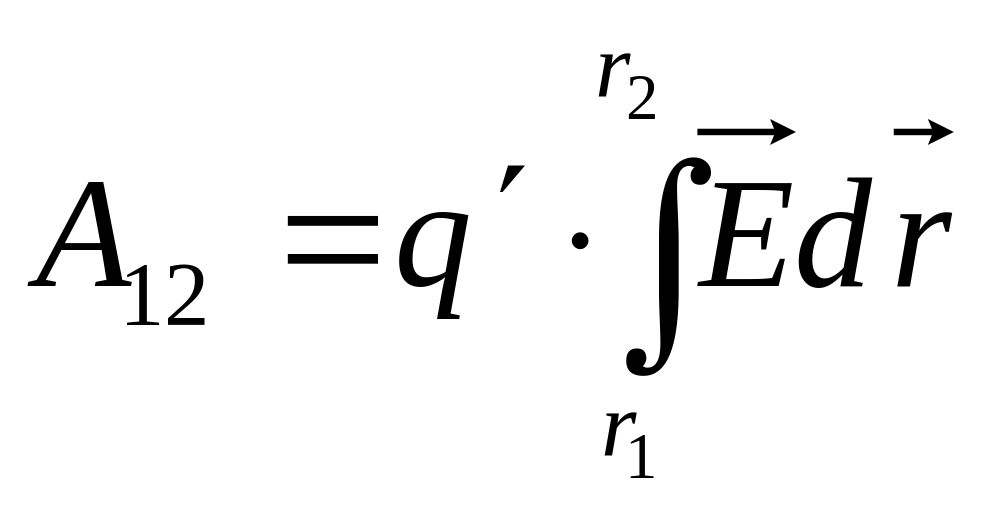– разность
потенциалов.
Физический смысл разности потенциалов – равен работе по перемещению единичного электрического заряда между двумя положениями.
.
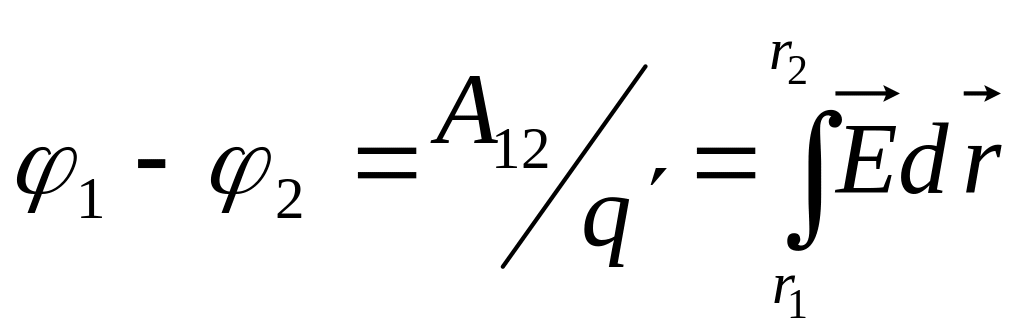Обычно принимает, что на
потенциал равен нулю, поэтому можно
говорить, что потенциал в данной точке
– это работа по перемещению единичного
электрического заряда на
:
.
Потенциал
– энергетическая
характеристика электрического поля.
.
При
:
и при
будет
.
.
.
Потенциал точечного заряда.
Р
.
.
.
.
Если
имеется заряженное тело, то
.
Если
заряды распределены по поверхности, то
.
Если
заряды распределены по линии, то
.
Если
перемещение равно 0, то есть по замкнутому
контуру, то
– циркуляция вектора напряжённости по
замкнутому контуру равна нулю.
Если в поле работа не зависит от формы пути, то это поле потенциальное.
Если а поле циркуляция по любому контуру равна 0, то поле безвихревое. Электрическое поле является и потенциальным и безвихревым.