
Государственное образовательное учреждение высшего профессионального образования
Санкт-Петербургский государственный морской технический университет
Кафедра систем автоматического управления и бортовых вычислительных комплексов
Воловодов С.К.
«Проектирование сау омт»
СПб
2009
Содержание
№ |
Название раздела |
стр |
1 |
Введение |
1 |
2 |
Кинематика. Системы координат. Углы Эйлера |
5 |
3 |
Преобразование линейных и угловых скоростей |
11 |
4 |
Параметры Эйлера |
13 |
5 |
Связь параметров и углов Эйлера |
16 |
6 |
Пример применения параметров Эйлера. |
17 |
7 |
Динамика. Механика Лагранжа-Кирхгофа |
|
8 |
Динамика твердого тела. Уравнения движения твердого тела |
|
9 |
Учет присоединенных масс жидкости |
|
10 |
Вычисление присоединенных масс |
|
11 |
Гидродинамические демпфирующие силы. Типы сил |
|
12 |
Восстанавливающие силы и моменты |
|
13 |
Уравнения движения ОМТ в векторно-матричной форме |
|
14 |
Модели технических средств управления движением |
|
15 |
Балансировочные режимы |
|
16 |
Основные виды движения ОМТ |
|
17 |
Примеры линеаризованных уравнений движения ОМТ. НК |
|
18 |
Судно на воздушной подушке |
|
19 |
Судно на подводных крыльях |
|
20 |
Автономный подводный аппарат |
|
21 |
Ветро-волновые возмущения. Регулярноя волнение. |
|
22 |
Силовые воздействия со стороны волнения.Редукционные коэффициенты. |
|
23 |
Нерегулярное волнение. Спектры морского волнения |
|
24 |
Алгоритмы расчета спектров процессов ОМТ на волнении |
|
25 |
Литература |
|
Введение
Предмет дисциплины «Проектирование САУ ОМТ» составляют системотехнические принципы построения этих систем и общие подходы к их проектированию на основе методов ТАУ (метод функций Ляпунова, методы теории оптимального управления для различных критериев и т.д.) и сопутствующих вычислительных процедур. Дисциплина читается для гр.3410 в осеннем и весеннем семестрах 4-го курса, в осеннем –экзамен, в весеннем –курсовой проект.
Объекты морской техники (ОМТ):
- надводные и подводные водоизмещающие ОМТ, многообъектные комплексы для проведения поисковых работ на шельфе и в океане, кабель-тросы, трубопроводы и т.д.(допускают позиционирование);
- объекты с динамическими принципами поддержания (позиционирование обычно невозможно);
- понятие ОМТ включает в себя как одиночные объекты, так и их совокупности.
ГОСТ 19176-85 «Системы управления техническими средствами корабля (ОМТ). Термины и определения» определяет систему управления техническими средствами ОМТ
как «функционально и конструктивно законченное изделие, обеспечивающее управление техническими средствами ОМТ» - СУ ОМТ (СУ МПО - системы управления морскими подвижными объектами).
СУ ОМТ – это система управления техническими средствами (исполнительными устройствами) ОМТ, которые обеспечивают постоянство или изменение по заданному закону кинематических параметров движения, характеризующих положение ОМТ в заданной системе линейных и угловых координат, а также скорость их изменения.
Разные типы ОМТ имеют различные системы управления. Тем не менее, СУ ОМТ имеют структурную общность обусловленную тем, что во всех случаях управляемым объектом является твердое тело, движущееся в воде, воздухе или на границе раздела водной и воздушной среды.
В общем случае система управления ОМТ включает в себя управляемый объект(ОМТ), исполнительные органы (активного или пассивного типа, которых должно быть достаточно для обеспечения требуемых режимов движения), датчики измерения кинематических параметров движения (линейные и угловые, включая наблюдатели для неизмеряемых координат) и вычислительные комплексы, обеспечивающие формирование сигналов управления исполнительными органами.
Синтез алгоритмов работы вычислительного комплекса, выбор числа и схемы размещения исполнительных устройств, построение измерительного комплекса составляют основные задачи проектирования СУ ОМТ, для решения которых привлекаются методы оптимального управления, математического моделирования, методы проектирования вычислительных сетей.
В значительной мере решение этих задач зависит от условий функционирования ОМТ.
Поэтому важным является построение математических моделей движения ОМТ в условиях ветро-волновых возмущений, необходимых для решения задач синтеза.
Литература
1.Ю.А.Лукомский, В.С.Чугунов. Системы управления морскими подвижными объектами. Л.Судостроение.1988.272с.
2.Пантов Е.Н.,Махин Н.Н., Шереметов Б.Б. Основы теории движения подводных аппаратов. Л.Судостроение.1973. 216с.
3. Автоматические подводные аппараты. М.Д.Агеев, Б.А.Касаткин и др. Л.Судостроение. 1981. 224с.
4. Thor I. Fossen. Guidance and control of ocean vehicles. John Wiley & Sons Ltd. NJ.1994. 480p.
Предмет изучения – навигация и управление океанскими подвижными объектами морской техники (ОМТ). Рассматривается проектирование для всех типов морских объектов подобных ПЛ, торпедам, неавтономным и автономным ПА, обычные суда, высокоскоростные суда (крыльевого типа и СВП), буровые платформы.
Примерами таких систем являются:
- системы управления скоростью,
- автопилоты, поддерживающие курс, путевой угол и пр.
- регуляторы разворотов,
- системы траекторной стабилизации,
- динамическое позиционирование,
- системы управления рулевыми приводами,
- системы управления стабилизаторами,
- системы демпфирования вибраций, наведенных морским волнением.
Термины навигации и управление МПО, как единого процесса.
Навигация - процесс определения требуемых курса, координат и скорости МПО, относительно некоторой системы координат (обычно земной), которыми должен следовать объект.
Управление – создание и применение к МПО необходимых сил и моментов , обеспечивающих движение на заданной траектории и стабилизацию движения. Это включает проектирование прямых и обратных связей в виде законов управления.
Пример системы автоматического проектирования пути [4] приведен на рис.1
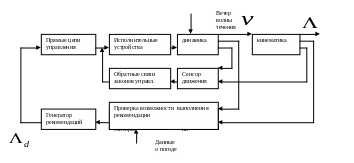
Рис.1
Проектирование автоматической всепогодной путевой системы для судна требует как продвинутого моделирования, так методов теории оптимального управления. Более того, требуется достаточно точная модель корабля и внешних возмущающих воздействиях.
Генератор рекомендаций использует погодные данные совместно с данными текущего состояния корабля, чтобы вычислить оптимальный путь.
Моделирование движения ОМТ
Моделирование ОМТ включает статику и динамику. Статика связана с равновесием тел в состоянии покоя или движения с постоянной скоростью. Динамика связана с ускоренным движением тел. Статика старейшая из инженерных наук. Более 2000 лет назад Архимедом (287-212 год до нашей эры) был открыт закон гидростатической плавучести. Этот результат является основой для анализа статической устойчивости МПО.
Изучение динамики началось много позднее, пока не были изобретены достаточно точные инструменты для измерения интервалов времени и перемещений объектов. Одни из первых (достаточно точных) время - измеряющих инструментов (водяные часы) были изобретены Леонардо да Винчи (1452-1519). Этот простой инструмент использовал факт, что интервал между капающими каплями воды является постоянным. Научная база динамики была обеспечена законами Ньютона, опубликованными в 1687г.
КИНЕМАТИКА
Системы координат. Углы Эйлера.
В качестве основных обычно рассматривают
неподвижную и связанную системы
координат. Неподвижная (земная)
![]() система
координат привязана к какой-либо точке
0 на земле и ориентирована осью
система
координат привязана к какой-либо точке
0 на земле и ориентирована осью
![]() на север (или на заданный курс); оси
на север (или на заданный курс); оси
![]() -
ортогональны и лежат в плоскости местного
горизонта, а
-
ортогональны и лежат в плоскости местного
горизонта, а
![]() -
направлена вверх (иногда вниз).
-
направлена вверх (иногда вниз).
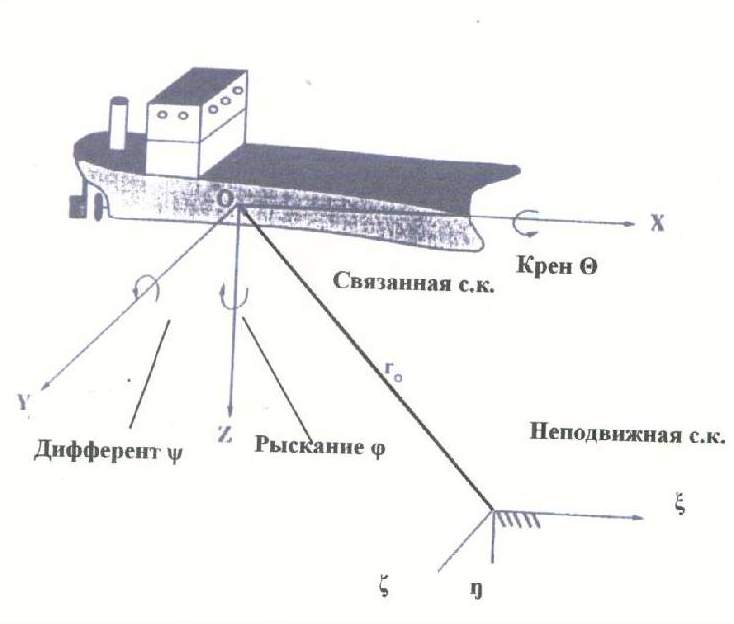
Рис.2
Связанная система координат привязана
к геометрическому центруОМТ (обычно к
центру величины или масс), а оси совпадают
с главными центральными осями инерции.
Ось
![]() лежит в диаметральной плоскости и
направлена в нос (для большинства ОМТ,
как то корабль, ПЛ, торпеда и пр.), ось
лежит в диаметральной плоскости и
направлена в нос (для большинства ОМТ,
как то корабль, ПЛ, торпеда и пр.), ось
![]() также
лежит в диаметральной плоскости и
направлена вверх, а ось
также
лежит в диаметральной плоскости и
направлена вверх, а ось
![]() перпендикулярна
плоскости
перпендикулярна
плоскости
![]() .
.
Возможна также промежуточная или полусвязанная система координат, которая характеризуется тем, что ее начало всегда совмещено с центром масс ОМТ, а координатные оси либо параллельны осям неподвижной системы координат , либо развернуты в горизонтальной плоскости на угол заданного курса (в такой системе удобнее рассматривать рыскание ОМТ на курсе).
Следует отметить, что в задачах синтеза законов управления до настоящего времени практически не учитывались особенности формирования управляющих сил для соответствующих систем координат (в которых действуют исполнительные органы). Пример: закон управления глубиной принятый на многих объектах формирует управление в связанной системе по замерам параметров движения в неподвижной (без соответствующего пересчета параметров движения в связанную систему координат).
Обозначения кинематических параметров Табл.1
Степень свободы |
Вид движения в связ СК |
Силы и моменты в связ. СК |
Линейные и угловые скорости в связ. СК |
Линейные и угловые (Эйлера) координаты в неподв.СК |
1
|
Вдоль оси 0х
|
|
|
|
2 |
Вдоль оси 0у |
|
|
|
3 |
Вдоль оси 0z |
|
|
|
4 |
Вращ. Вокруг 0х |
|
|
|
5 |
Вращ. Вокруг 0у |
|
|
|
6 |
Вращ. Вокруг 0z |
|
|
|
В дальнейшем вектор линейных и угловых
координат в неподвижной системе координат
обозначаем
![]() .
Иногда будем выделять вектор линейных
перемещений
.
Иногда будем выделять вектор линейных
перемещений
![]() и
вектор ориентации (углы Эйлера)
и
вектор ориентации (углы Эйлера)
![]() .
.
Совокупный вектор линейных и угловых
скоростей в связанной системе будем
обозначать
![]() ,
(
,
(![]() )а
вектор управляющих сил и моментов (в
связанной системе координат) -
)а
вектор управляющих сил и моментов (в
связанной системе координат) -
![]() .
.
Примеры векторно-матричного представления систем и объектов. Системы ДУ.
Структура принятой формы записи уравнений динамики и кинематики (без учета ветро-волновых сил):
![]() (1)
(1)
Углы Эйлера
Линейные перемещения МПО относительно неподвижной системы (earth-fixed) координат определяется преобразованием вектора скорости
![]() ,
обратное преобразование
,
обратное преобразование
![]() .
.
Аналогично
![]() ,
,![]() .
.
И в общем случае
![]() ,
,
![]() .
.
Теоремы Эйлера о вращении. Единичные повороты.
Пусть один и тот же вектор
![]() зафиксирован в системе
зафиксирован в системе
![]() (неподвижной) и как вектор
(неподвижной) и как вектор
![]() в системе
в системе
![]() (связанной).
(связанной).
Система
развернута
по отношению к системе
на угол
![]() относительно оси вращения, положение
которой задано единичным вектором
относительно оси вращения, положение
которой задано единичным вектором
![]() в
неподвижной с.к., рис.3.
в
неподвижной с.к., рис.3.
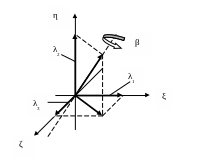
Рис.3
Тогда вектор может быть выражен [4] соотношением
![]()
Переход от вектора к вектору в матричной форме имеет вид
![]() ,
где
,
где
![]() -
матрица вращения, м.б. получена заменой
единичной
матрицей. Тогда
-
матрица вращения, м.б. получена заменой
единичной
матрицей. Тогда
![]() ,
где (2)
,
где (2)
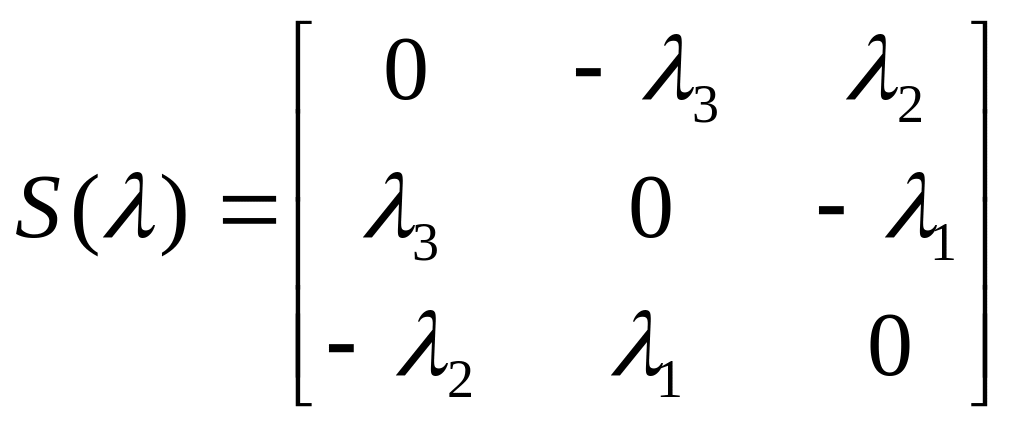 -кососимметрическая
матрица.
-кососимметрическая
матрица.
![]() определяется
следующим образом
определяется
следующим образом
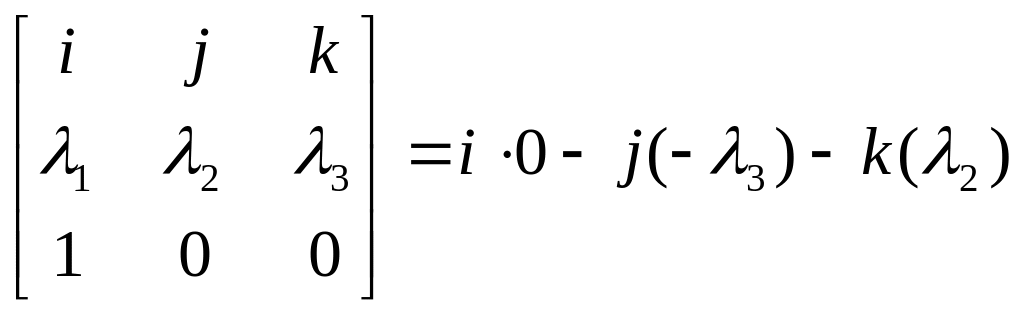 -
1-й столбец матрицы
-
1-й столбец матрицы
![]() ;
;
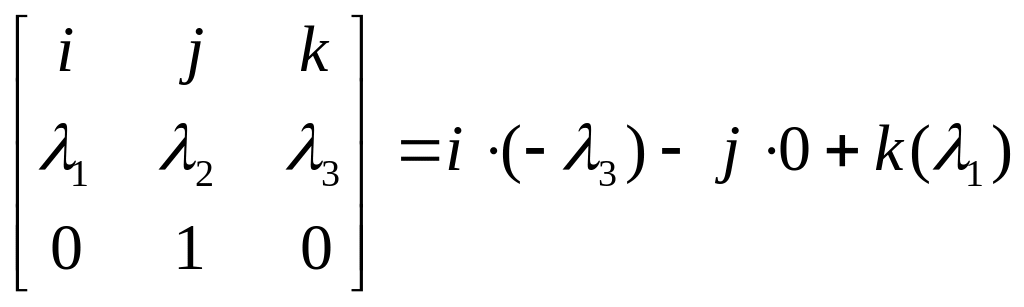 -
2-й столбец матрицы
;
-
2-й столбец матрицы
;
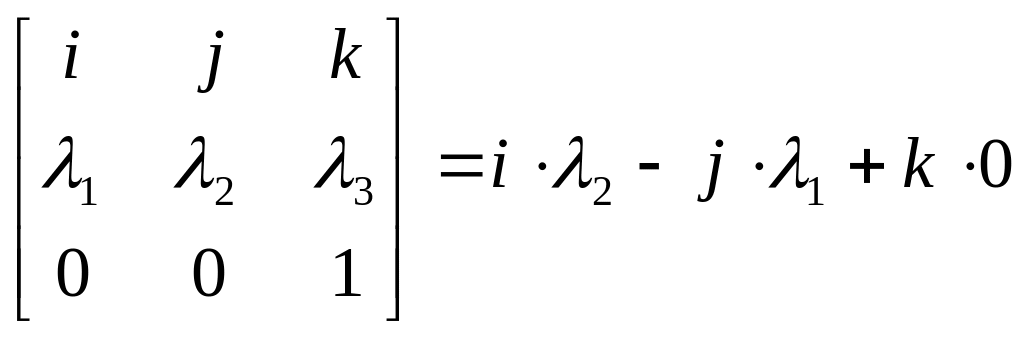 -
3-й столбец матрицы
.
-
3-й столбец матрицы
.
Матрица
![]() называется
кососимметрической, т.к.
называется
кососимметрической, т.к.
![]() .
.
 .
.
Тогда
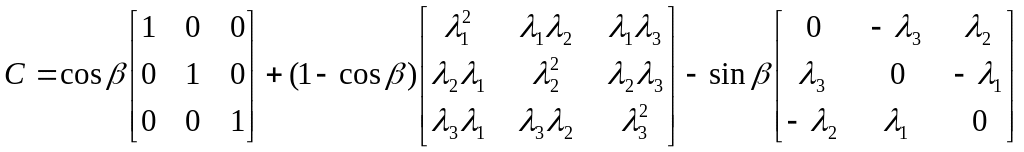 .
(2)
.
(2)
Матрица С состоит из следующих элементов
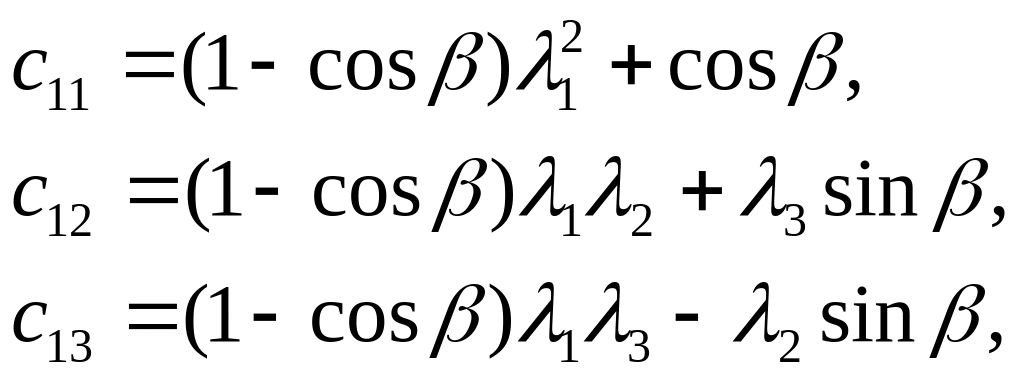
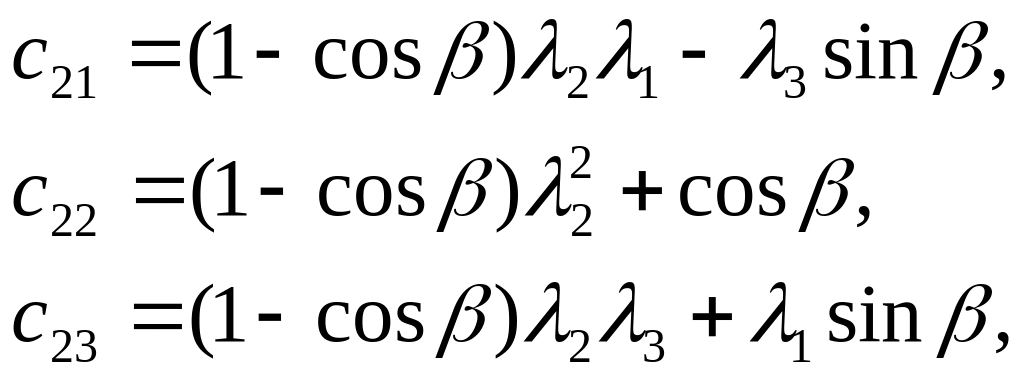 (3)
(3)
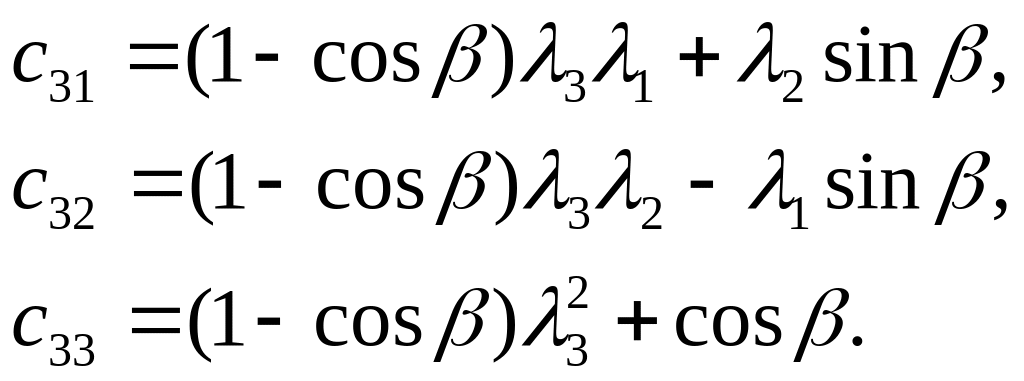
И удовлетворяет соотношениям
![]() .
.
Матрицы вращения (одиночных поворотов).
Матрицы вращения относительно отдельных осей на некоторые углы (углы Эйлера)
получаются подстановкой
![]() (соответственно
повороты
(соответственно
повороты
![]() ).
).
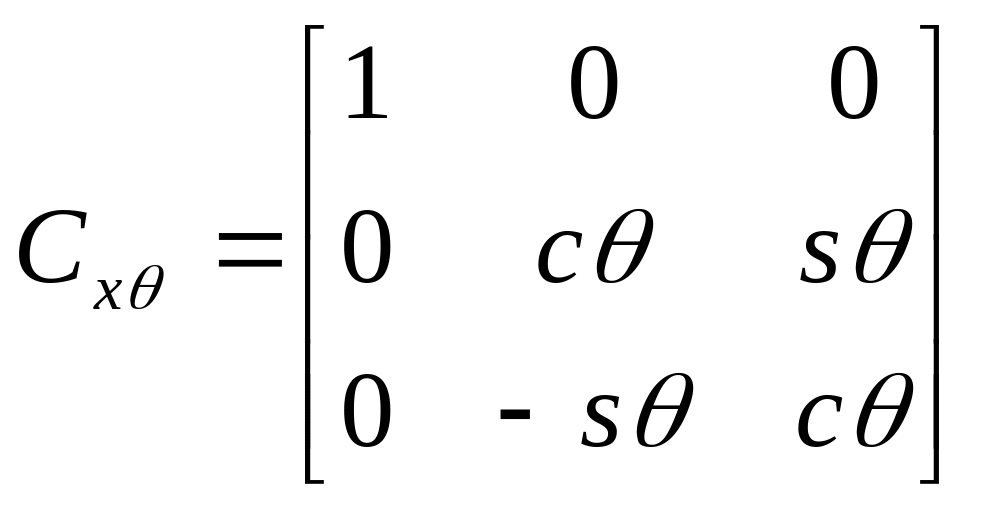 ,
,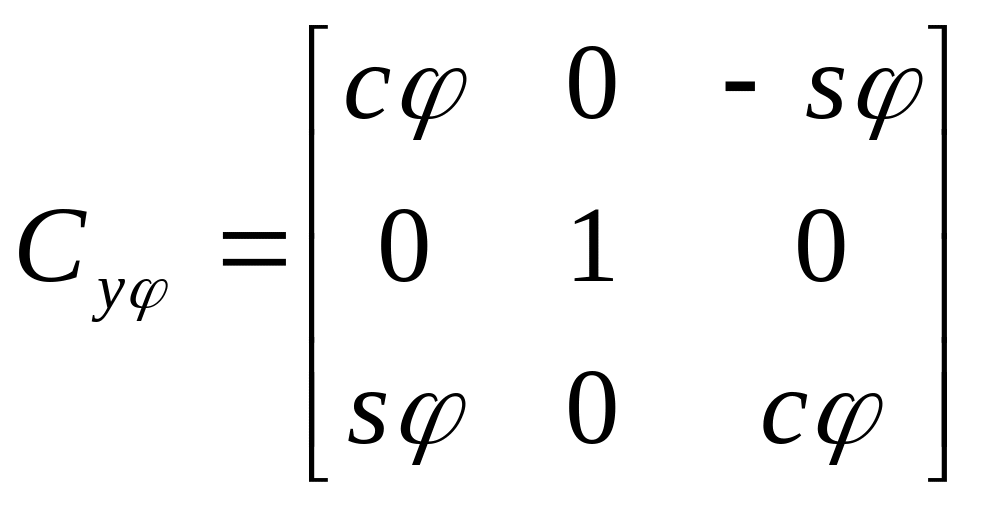 ,
,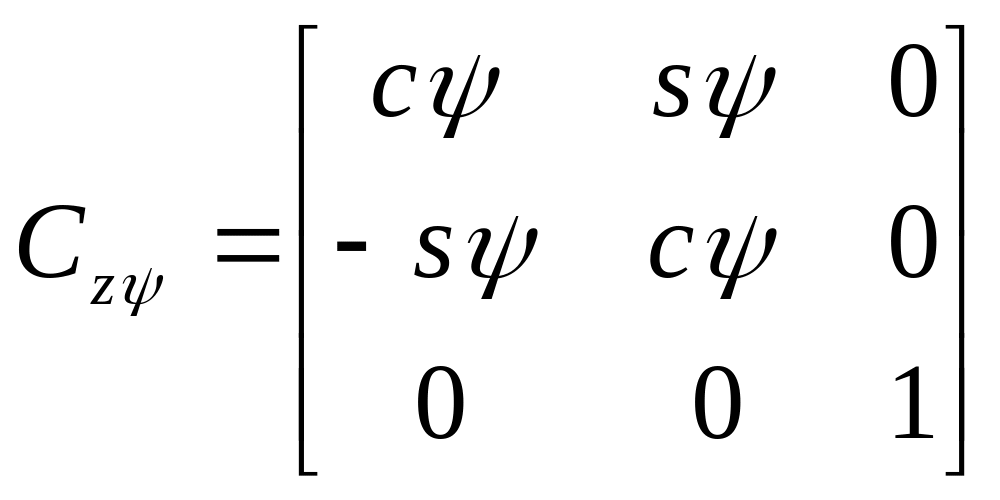 .
(4)
.
(4)
Матрицы вращения (для плоских поворотов) также могут быть построены на основании простых перестроений векторов из одной системы координат в другую развернутую на некоторый угол.
Пример вычисления матрицы
![]() показан
на рисунке. Оси
и
совмещены
и направлены к нам. Разворачиваем
связанную с.к. вокруг оси 0х на угол
,
см. рис.4
показан
на рисунке. Оси
и
совмещены
и направлены к нам. Разворачиваем
связанную с.к. вокруг оси 0х на угол
,
см. рис.4
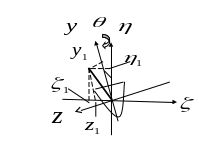
Рис.4
Связь проекций дается соотношениями
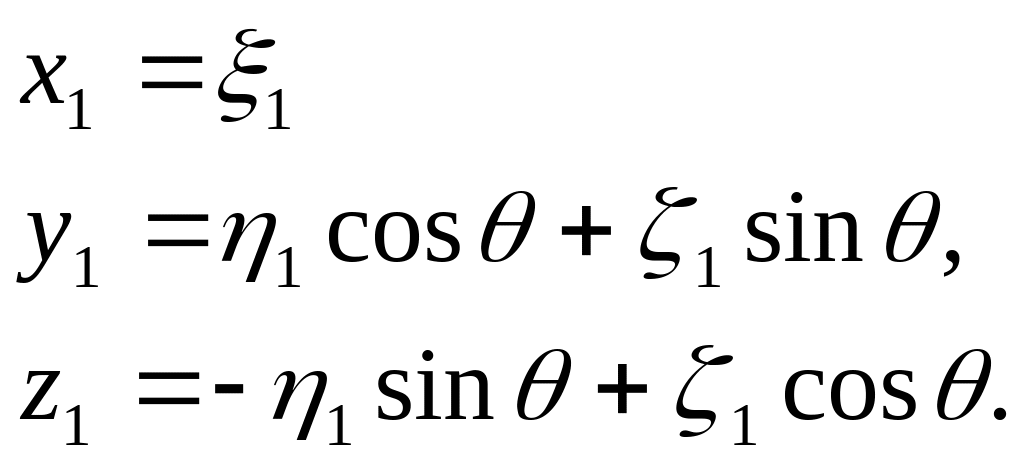
Тогда матрица, связывающая проекции в связанной СК с проекциями в неподвижной, имеет вид
![]()
![]()
 .
.
Вычисление матрицы
![]() поясняется
рисунком 5.
поясняется
рисунком 5.
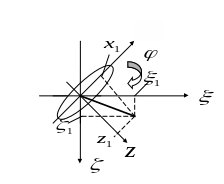
Рис.5
Из рисунка следует
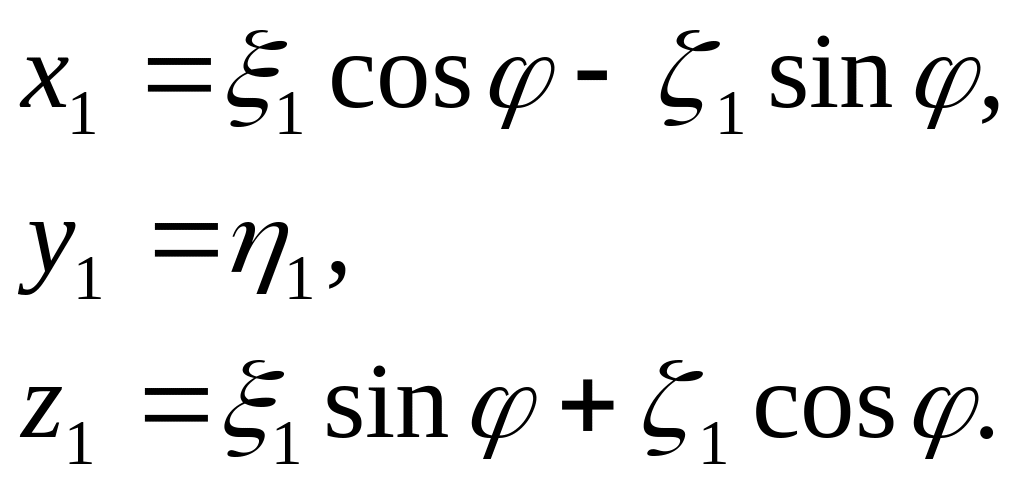
Тогда матрица имеет вид
![]()
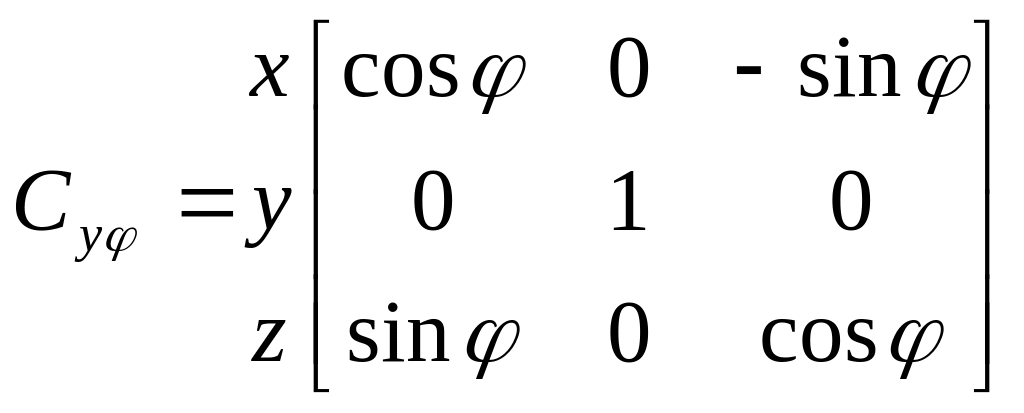 .
.
Вычисление матрицы
![]() поясняется
след. рисунком 6.
поясняется
след. рисунком 6.
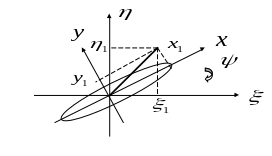
Рис.6
Также справедливы соотношения

И матрица
![]() имеет
вид
имеет
вид
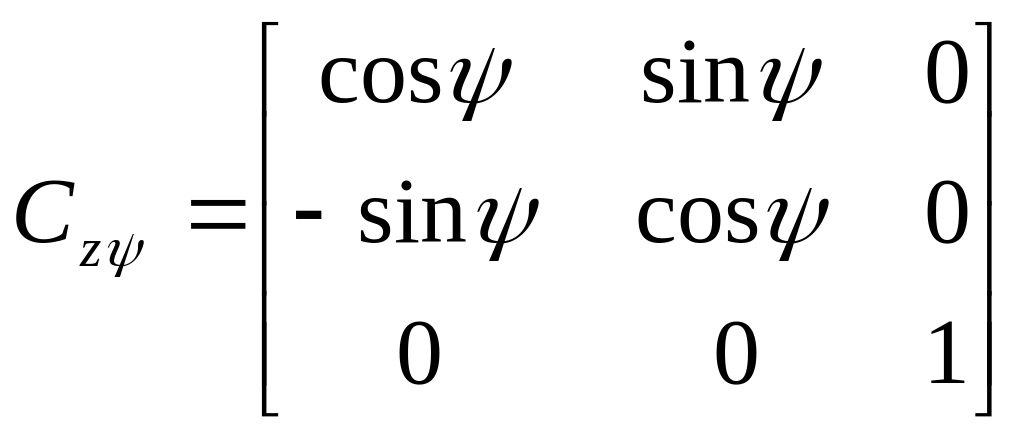 .
.
В дальнейшем для простоты используем
обозначения
![]() ,
аналогично для функций
,
аналогично для функций
![]() .
.
Матрица преобразования линейных координат при поступательном движении
Как показано выше матрица преобразования линейных координат из неподвижной в связанную имеет вид
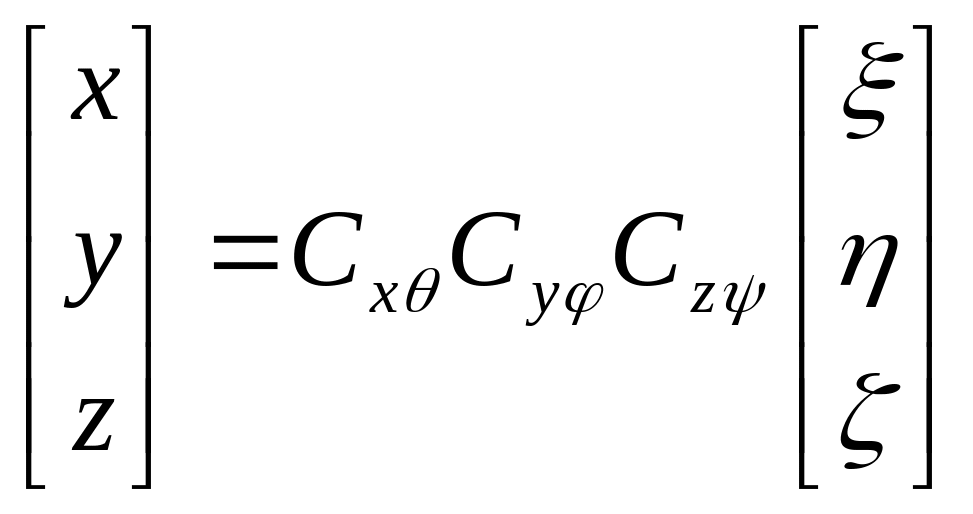 ,
аналогично линейные скорости
,
аналогично линейные скорости
 .
.
Нас интересует обратное преобразование
(с учетом, что
![]() )
)
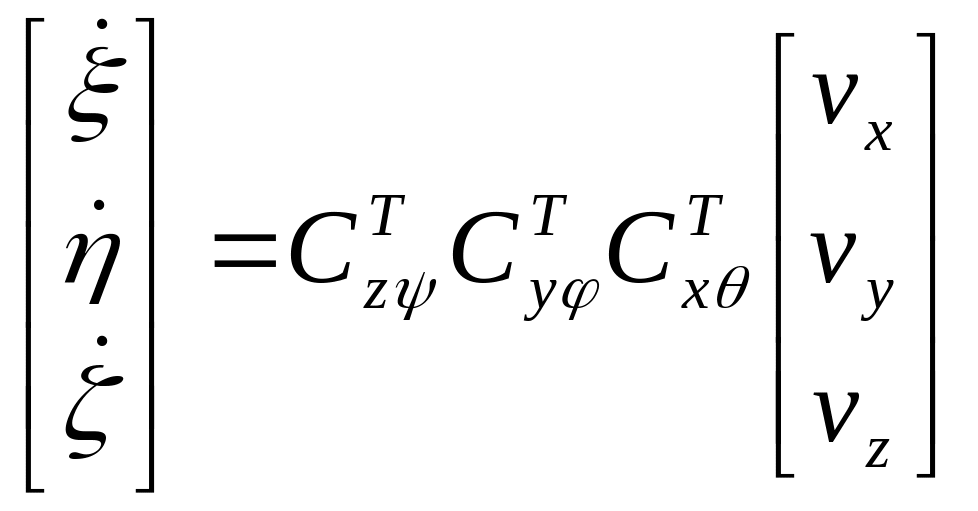 .
.
Таким образом, можно рассматривать матрицы с различной последовательностью поворотов:
1.![]() ,
(вход – вектор в связанной с.к., выход в
неподвижной с.к.) и
,
(вход – вектор в связанной с.к., выход в
неподвижной с.к.) и
матрицу
![]() (вход
– вектор в неподвижной с.к., выход – в
связанной с.к.),
(вход
– вектор в неподвижной с.к., выход – в
связанной с.к.),
![]() .(обратная
матрица в данном случае равна
транспонированной).
.(обратная
матрица в данном случае равна
транспонированной).
Тогда, имеем
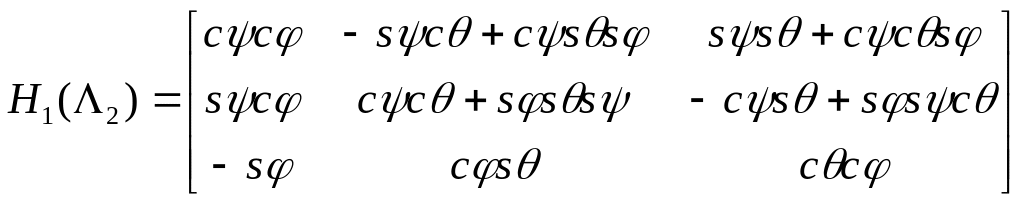 .
(5)
.
(5)
Поскольку
 ,
,
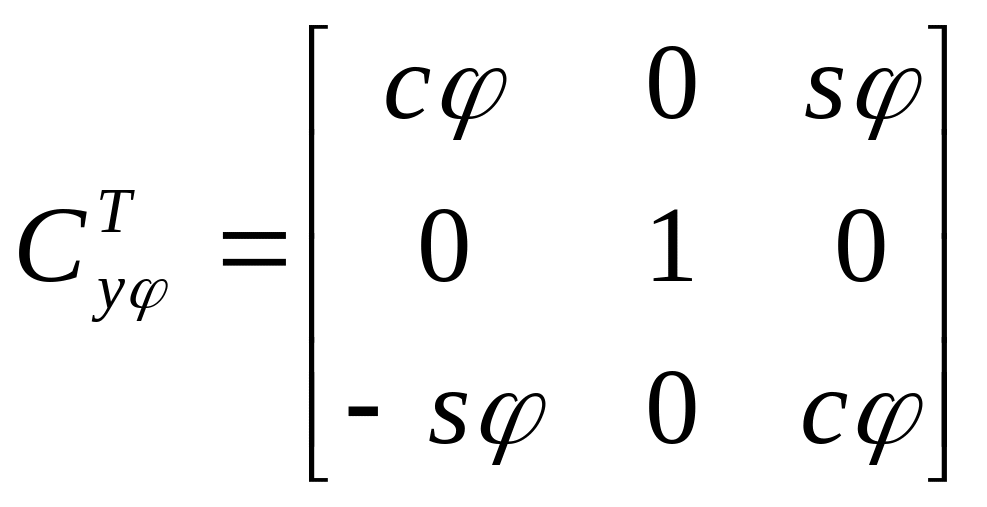 ,
,
 .
.
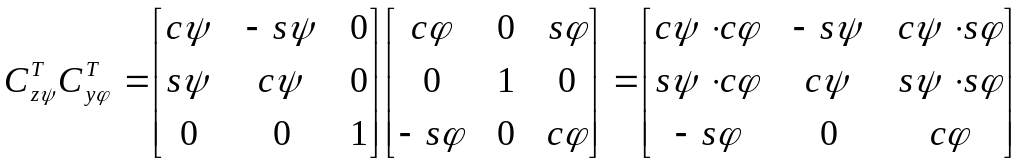 ,
,
 .
.
Окончательно
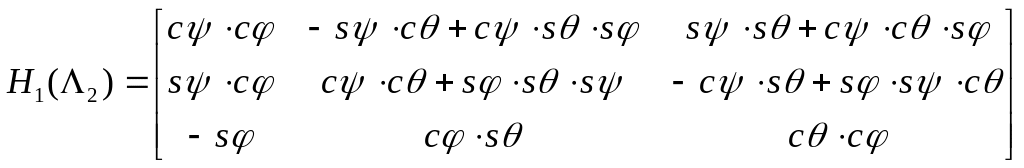 .
.
2. В зависимости от последовательности
поворотов матрица
![]() может
быть различной. Так, если
может
быть различной. Так, если
![]() , то имеем
, то имеем
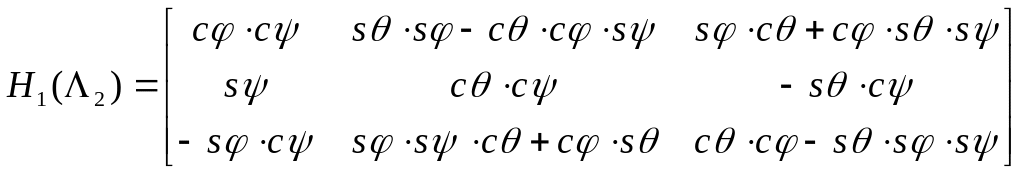 .
.
Преобразование вектора угловых скоростей при вращательном движении
или
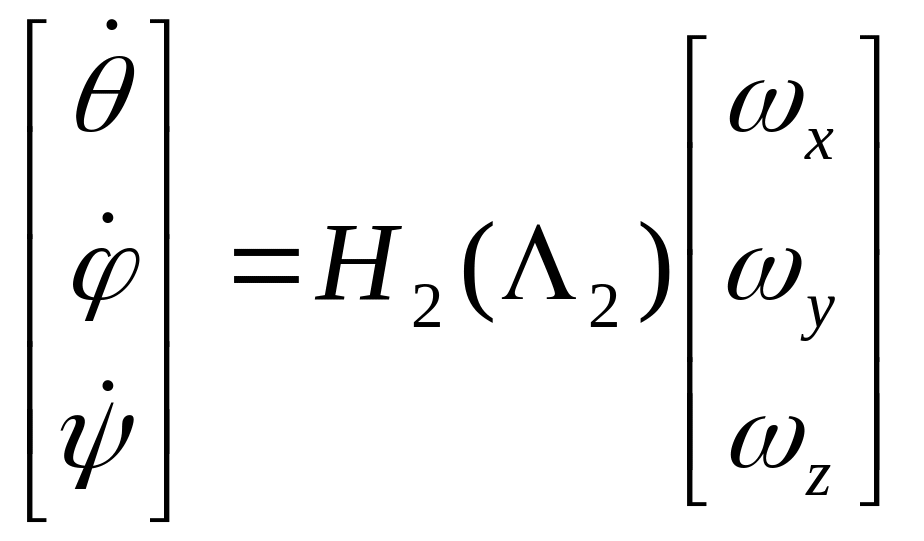 .
.
В силу принятой последовательности
поворотов![]() ,
имеем
,
имеем
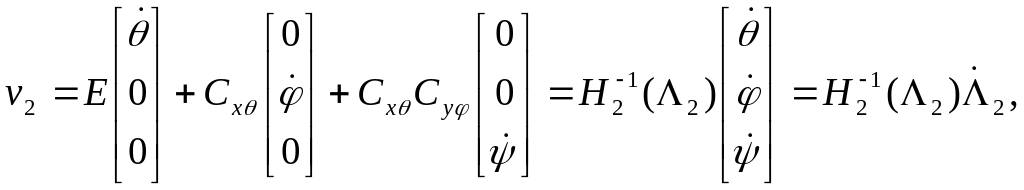 ,
,
где
,
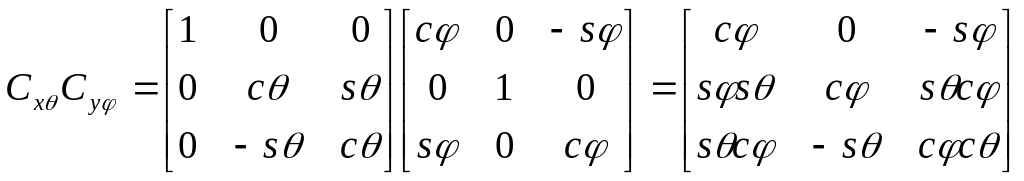 .
.
Тогда

 ,
,
![]() ,
,
а
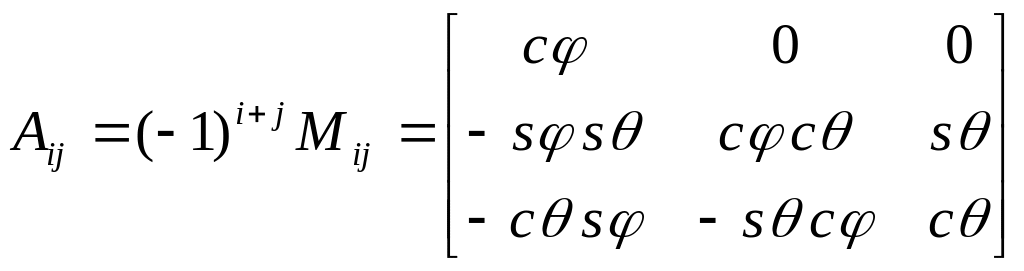 ,
и окончательно
,
и окончательно
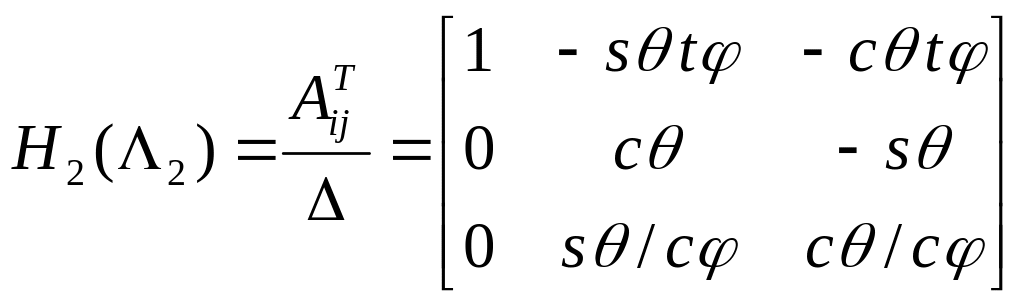 .
(6)
.
(6)
Видно, что элементы 2-го и 3-его столбцов
имеют особую точку при
![]() .
.
2.Если последовательность поворотов![]() ,то
,то
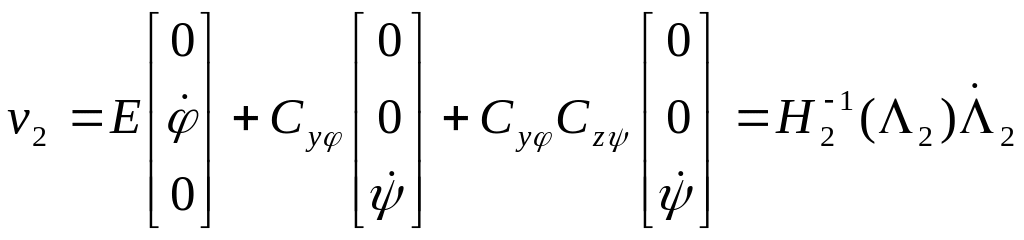 ,
и ,соответственно
,
и ,соответственно
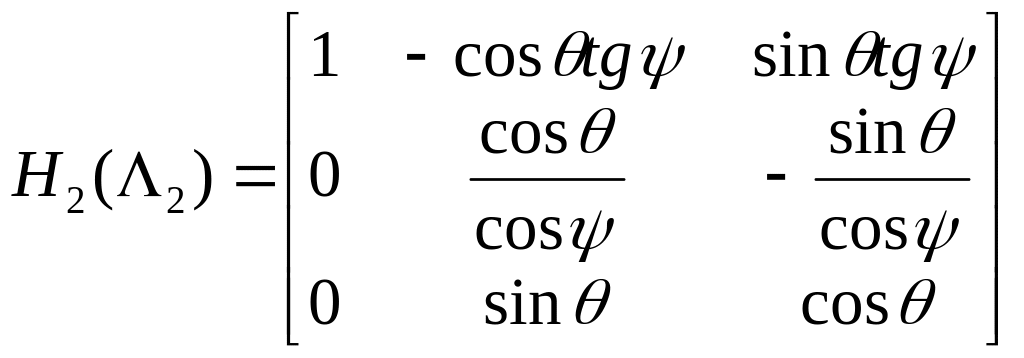 .
(7)
.
(7)
Тогда особая точка имеет место при
![]()
Окончательно
![]() .
.
Для расчета параметров движения в
неподвижной системе координат могут
использоваться соотношения полученные
при разных последовательностях поворотов.
Если матрица становится особенной, то
следует переходить к соотношениям, где
данная особенность отсутствует, поскольку
одновременно углы Эйлера обычно не
примают значения
![]()
Указанные уравнения зачастую используются
в навигационных задачах (определение
собственных координат в неподвижной
земной системе) – навигация с помощью
БИНС (бесплатформенных инерциальных
навигационных систем) при этом замеры
проекций скорости![]() пересчитываются в проекции скорости
пересчитываются в проекции скорости
![]() в
неподвижной системе координат на
основании соотношений(5,б,7).
в
неподвижной системе координат на
основании соотношений(5,б,7).
Следует отметить, что в последнем случае
при
![]() матрица
матрица
![]() также
становится особенной. Кроме того
также
становится особенной. Кроме того
![]() .
.
Для надводных судов это не имеет особого значения, однако для ПА и самолетов это может представлять проблему. В этом случае для критических углов или можно использовать систему с другой последовательностью поворотов или использовать представление кинематики в параметрах Эйлера.
Параметры Эйлера
Вместо углов Эйлера используются четыре параметра (единичных кватернионов).
Понятие кватерниона
Кватернион
![]() представляет
собой вектор
представляет
собой вектор
![]() ,
сформированный 3-мя ортогональными
векторами и 1
,
сформированный 3-мя ортогональными
векторами и 1
![]() и
с использованием чисел
и
с использованием чисел
![]() .
.
Используем соотношение (2)
Параметры Эйлера или единицу кватернионов определим как
![]() ,
,
причем вектор
![]() связан
с параметрами Эйлера соотношениями:
связан
с параметрами Эйлера соотношениями:
![]() ;
;
![]() ,
,
![]() .
.
Соответственно
 .
.
Параметры Эйлера удовлетворяют соотношению
![]() или
или
![]() .
.
Тогда элементы матрицы
![]() определяются
из соотношений:
определяются
из соотношений:
![]()
![]() .
.
![]()
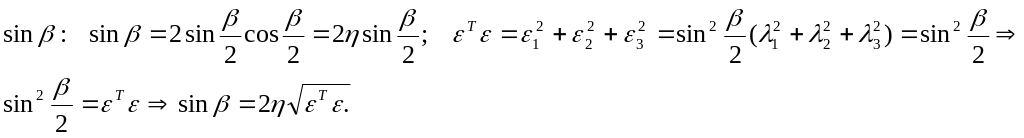

Преобразующая матрица для параметров Эйлера в этом случае имеет вид:
![]() (
(![]() )
)
Составляющие матрицы :
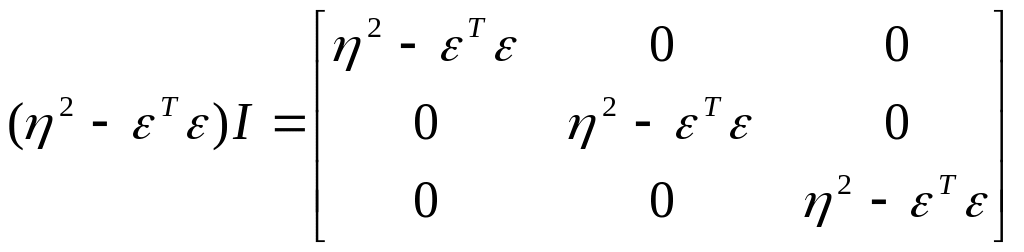 ,
,
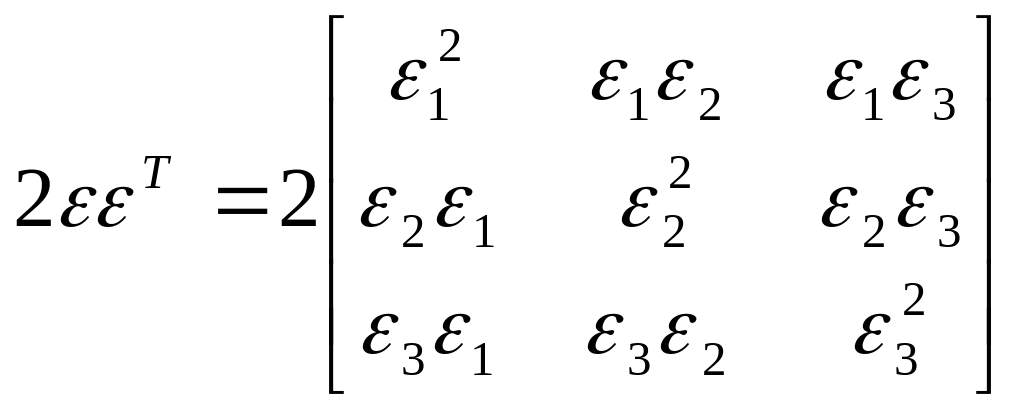 ,
,
 .
.
Преобразование линейных скоростей.
![]() ,
(скорости
,
(скорости
![]() постоянно измеряются)
постоянно измеряются)
где
![]() ,
тогда
,
тогда
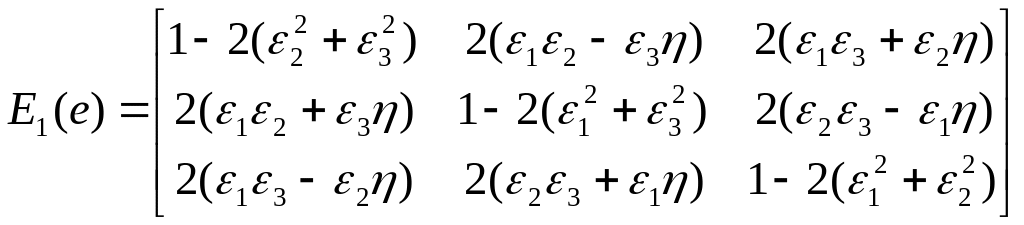 ,
(8)
,
(8)
![]() .
Уравнения для вектора
.
Уравнения для вектора
![]() приводятся
ниже.
приводятся
ниже.
Преобразование угловых скоростей.
Матрица удовлетворяет соотношению
![]() .
.
Продифференцировав, получим
![]() .
.
Обозначим
![]() -
любая кососимметрическая матрица ,т.е.
-
любая кососимметрическая матрица ,т.е.
![]() ),
),
Домножив обе части ур-ния на
![]() ,
тогда получим (с учетом, что
,
тогда получим (с учетом, что
![]() )
)
![]() ,
,
Пусть
 .
.
Тогда предыдущее уравнение можно раскрыть
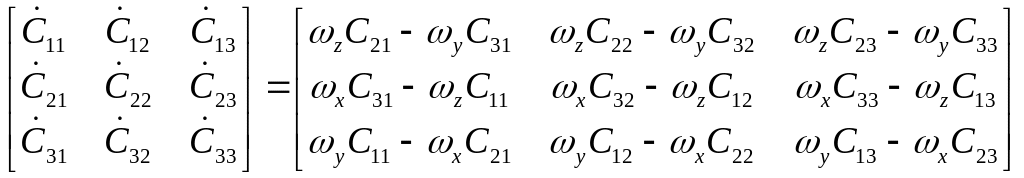 .
.
Подстановка в уравнение параметров
![]() из уравнения (
)
(выше для С) приводит к уравнению для
вычисления вектора
из уравнения (
)
(выше для С) приводит к уравнению для
вычисления вектора
![]() ,
,
 ,
,
![]() (9)
(9)
Соответственно кинематические уравнения движения можно записать в виде
![]()
![]()
![]()
![]() .
(10)
.
(10)
![]() ,
,
![]()
Алгоритм вычисления параметров Эйлера
1.
![]() .
Вычисляются (или определяются по GPS)
начальные значения
.
Вычисляются (или определяются по GPS)
начальные значения
![]() и
и
![]() (см.ниже).
(см.ниже).
2. Методом Эйлера вычисляются значения переменных на следующем шаге
![]()
![]() -
шаг интегрирования.
-
шаг интегрирования.
3. Нормализация:
![]()
4.
![]() -приращение
переменной
-приращение
переменной
![]() и
возврат к п.2.
и
возврат к п.2.
Связь между параметрами Эйлера и углами Эйлера

или
 .
.
Откуда
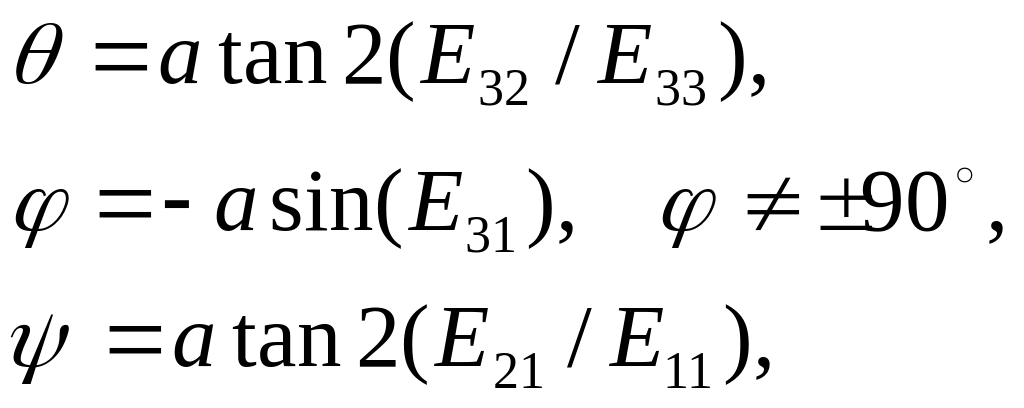 (11)
(11)
где
![]() -
вычисляется в четвертом квадранте для
вещественных
-
вычисляется в четвертом квадранте для
вещественных
![]() по
формуле
по
формуле
![]() ,
,
![]() .
.
Вычисление начальных условий для интегрирования уравнений для параметров Эйлера
Может осуществляться на основании замеренных в начальный момент углов Эйлера:
Возможны два способа:
1-й способ:
Поскольку
![]()
то
![]() ,
,
![]() .
.
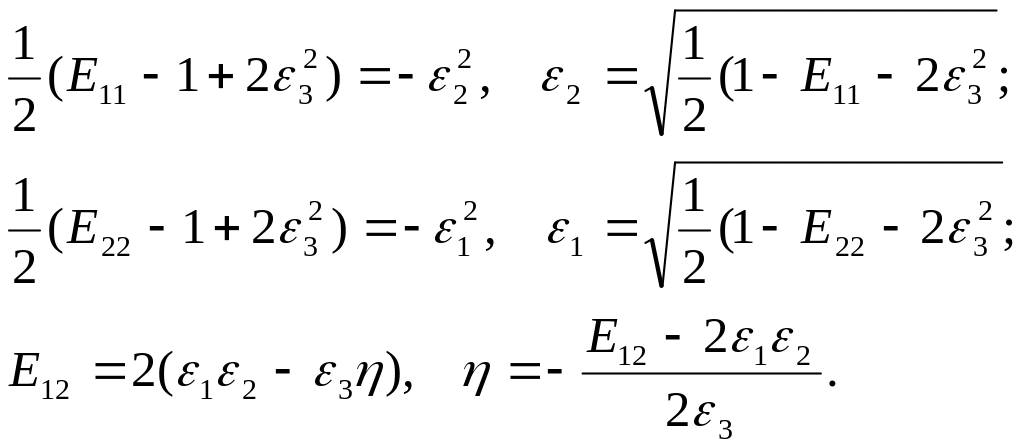
С последующей нормировкой параметров
![]() .
.
2-й способ.
1. Предположим, углы Эйлера известны.
Тогда матрица преобразования
![]() ,
соответствующая этим величинам имеет
вид
,
соответствующая этим величинам имеет
вид
 .
.
2. След матрицы
![]() вычисляется по ф-ле
вычисляется по ф-ле
![]()
3. Пусть, для
![]() есть
индекс
есть
индекс
![]() ,соответствующий
,соответствующий
![]() .
.
4. Определим
![]() .
.
Знак
![]() м.б.
выбран положительным или отрицательным.
м.б.
выбран положительным или отрицательным.
5. Вычислим другие три величины по формулам
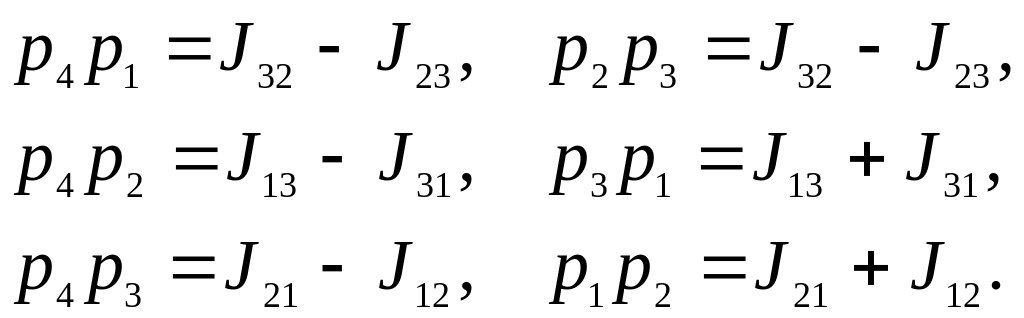
Например, выбран параметр
![]() ,
тогда используются уравнения, содержащий
этот параметр.
,
тогда используются уравнения, содержащий
этот параметр.
6. Вычислить параметры
![]() из
соотношений
из
соотношений
![]()
Пример применения параметров Эйлера в навигационных системах.
