9.Сущность и значение средних показателей. Виды степенных средних.

Средние величины - статистические показатели, которые дают сводную (итоговую) характеристику массовых общественных явлений, так как строятся на основе большого количества индивидуальных значений варьирующего признака.

Средняя величина отражает то, что характерно для единиц изучаемой совокупности. Они тесно связаны с законом больших чисел. Сущность этой зависимости заключается в том, что при большом числе наблюдений случайные отклонения от общей статистики взаимопогашаются и в среднем более отчетливо проявляется статистическая закономерность.

Средняя величина - обобщающий показатель, характеризующий уровень варьирующего признака в расчете на единицу однородной совокупно; в конкретных условиях места и времени.

Исчисление средних величин предполагает выполнение следующих требований:

1) качественная однородность совокупности, по которой исчислена средняя. Исчисление средних величин должно основываться на методе группировок, обеспечивающем выделение однородных, однотипных явлений;

2) исключение влияния на исчисление средней величины случайных, сугубо индивидуальных причин и факторов. Достигается в том случае, когда исчисление средней основывается на массовом материале, в котором проявятся действие закона больших чисел и все случайности взаимно погашаются;

3) при вычислении средней величины важно установить цель ее расчета и так называемый определяющий показатель (свойство), на который она должна быть ориентирована. Определяющий показатель может выступать в виде суммы значений осредняемого признака, сунны его обратных значений и т. п. Связь между определяющим показателем и средней выражается в следующем: если все значения осредняемого признака заменить их средним значением, то сумма или произведение в этом случае не изменит определяющего показателя. С помощью метода средних решаются следующие задачи:

1) характеристика уровня развития явлений;

2) сравнение двух или нескольких уровней;

3) изучение взаимосвязей социально-экономических явлений;

4) анализ размещения социально-экономических явлений в пространстве.

К степенным средним относятся такие наиболее известные и часто применяемые виды, как средняя геометрическая, средняя арифметическая и средняя квадратическая. Остановимся на степенных средних. Степенные средние в зависимости от представления исходных данных могут быть простыми и взвешенными. Простая средняя считается по не сгруппированным данным и имеет следующий общий вид:

,

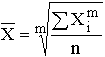Взвешенная средняя считается по сгруппированным данным и имеет общий вид        

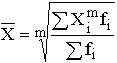
Общие формулы расчета степенных средних имеют показатель степени (m). В зависимости от того, какое значение он принимает, различают следующие виды степенных средних: средняя гармоническая, если m = -1; средняя геометрическая, если m –> 0; средняя арифметическая, если m = 1;  средняя квадратическая, если m = 2; средняя кубическая, если m = 3.

Если рассчитать все виды средних для одних и тех же исходных данных, то значения их окажутся неодинаковыми. Здесь действует правило мажорантности средних: с увеличением показателя степени m увеличивается и соответствующая средняя величина:

В статистической практике чаще, чем остальные виды средних взвешенных, используются средние арифметические и средние гармонические взвешенные.

Среднюю гармоническую применяют для расчетов тогда, когда в качестве весов используются не единицы совокупности – носители признака, а произведения этих единиц на значения признака (т.е. m = Xf). Формула средней геометрической

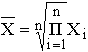
используется чаще всего при расчете среднего значения по индивидуальным относительным величинам динамики.