28. Интегрирование линейных однородных дифференциальных уравнений второго порядка.

- постоянные. Берется . Решая, получаем

- общее решение.

ЛОДУ решают составляя характеристические уравнения:

Случаи:

• Различные корни

- общее решение ЛОДУ

• Кратные характеристические корни,

- общее решение ЛОДУ

• Случай комплексных характеристических корней

Для неоднородных

, где - правая часть.

29. Решение линейных неоднородных дифференциальных уравнений со специальной правой частью.

Случаи:

• 

- частное решение ЛНДУ

- корень - кратность среди корней ЛОДУ

- степень многочлена.

… - подстановка в ЛОДУ для нахождения коэффициентов.

- общее решение ЛНДУ, где – решение ЛОДУ

• 

• 

30. Системы дифференциальных уравнений, разрешенных относительно производных. Теорема Коши. Метод исключения для решения систем дифференциальных уравнений.

Системой ДУ называется совокупность ДУ, каждое из которых содержит независимую переменную искомой функции и их производные. Система ДУ разрешенная относительно производной:

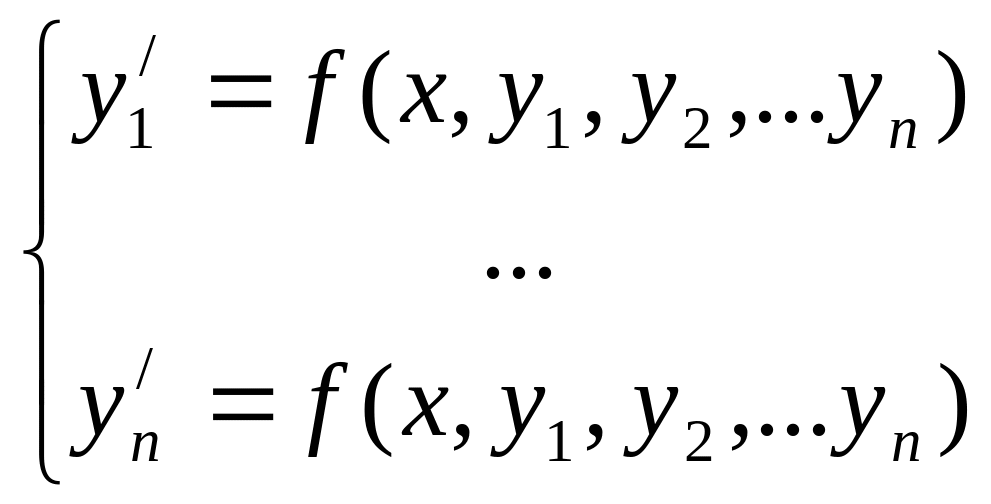называется нормальная форма системы ДУ.

Решением системы называется совокупность - функций удовлетворяющих каждой из уравнений системы.

Теорема Коши. Если в системе все - непрерывны вместе со всеми частными производными по в некоторой области Д (n+1) мерного пространства, то в каждой точке -существует единственное решение системы удовлетворяющее начальным условиям.

Решение

Метод исключения.

Алгоритм для случая двух функций.

• Дифференцируем одно из уравнений обе части по х.

• Заменяем и

• Из 1-ого уравнения системы можно выразить через остальное.

• - подставить во второе уравнение.

• Получаем 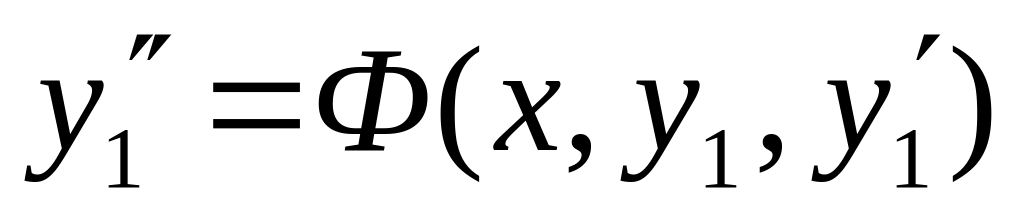- решаем. Получаем

• Подставляем и в 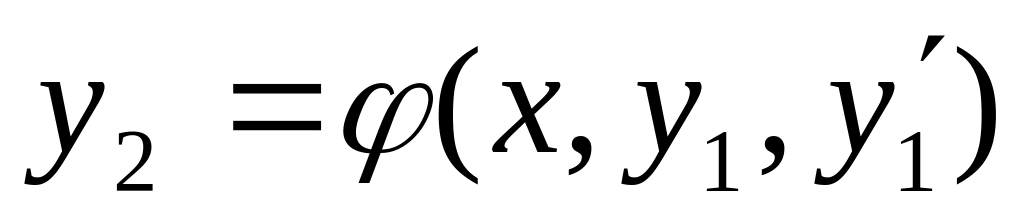решаем

31. Случайные события и их вероятности.

Случайный исход – любой наблюдаемый результат в том или ином опыте. Множество элементарных исходов (Ω) – множество всех взаимоисключающих возможных исходов, результат – только 1 исход.

Любое подмножество A множество элементарных исходов Ω интерпретируется, как случайное событие.

Невозможное событие – это событие, совпадающее с пустым множеством Ø.

Достоверное событие – событие, которое совпадает со всем множеством Ω.

Два события называются совместными (несовместными), если в результате опыта возможно (невозможно) их совместное появление.

В общем случае Ω м/б дискретным или непрерывным.

32. Операции над событиями. Классическое определение вероятности. Геометрическое определение вероятности.

• Сумма (объединение 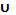) – событие состоит из элементарных исходов, входящих или в A, или в B (не исключающее логическое «или»).

• Произведение (перечисление ) – событие, состоящее из элементарных исходов, принадлежащих и A, и B (логическое «и»).

• Разность (\) – событие, состоящее из элементарных исходов, принадлежащее A, но не принадлежащее B.

• Отрицание – противоположное событие (Ā) не принадлежит A.

События образуют полную группу событий если и .

Равные события, если всякий раз, когда наступает одно из них, наступает и другое.

Классическое определения вероятностей событий: Пусть A – случайное событие некоторого опыта, предположим, что он проведён n раз: n(A), тогда вероятностью будет , где A – отношение удвл. Исх. Ко всем.

Геометрическая вероятность – пусть множеством эл. исходов служит множество точек M фигуры . Мера .