15. Интегрирование функции комплексного переменного. Сведение интеграла к сумме криволинейных интегралов второго рода.

Определение интеграла от ФКП: Предел интегральной суммы Римана

д ля функции по кривой АВ, если он не зависит ни от способа разбиения кривой АВ на элементарные дуги , ни от способа выбора точек t_m на каждой элементарной дуге, при условии, что n → ∞, λ= max|Δz_m|→0, называют интегралом от функции f(z) по кривой АВ и обозначают

Т еорема о связи криволинейных интегралов и интеграла от ФКП: Если действительная u(x, y) и мнимая v(x, y) части функции f(z)=u(x,y) + iv(x,y) непрерывны на кусочно-гладкой кривой АВ, то интеграл от функции f(z) по кривой АВ равен сумме двух криволинейных интегралов второго рода от действительных функций:

Следствие: Если кривая АВ задана параметрически дифференцируемыми функциями

Свойства:

16. Теорема Коши. Первообразная и неопределенный интеграл. Формула Ньютона-Лейбница.

Область называется односвязной, если она ограничена замкнутой не самопересекающейся линией.

Теорема Коши. Если функция аналитична в односвязной области Д, то интеграл вдоль кривой L , если кривая L лежит в области Д полностью.

Следствие: если функция аналитична в односвязной области Д, то интеграл от неё зависит от начальной точки и конечной точки интегрирования.

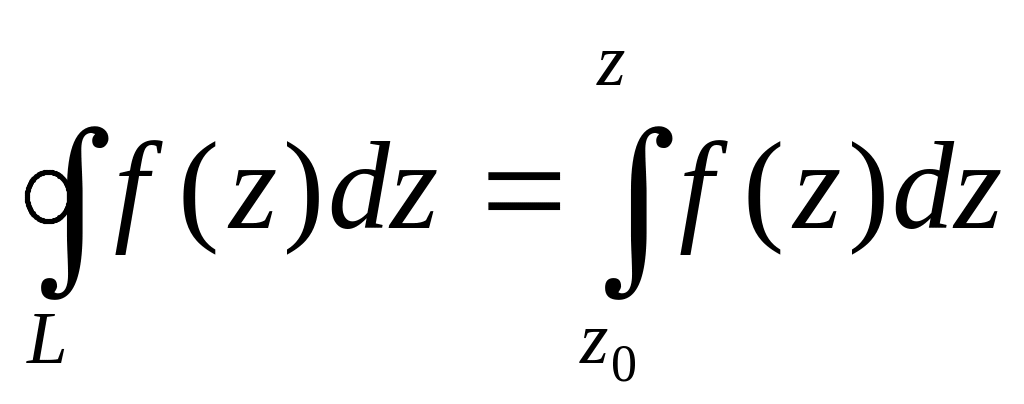
Функция называется первообразной для функции если выполняется . Если аналитическая, то тоже.

Если - первообразная, то и тоже.

Неопределенным интегралом от функции называется , так же вытекает формула Ньютона-Лейбница

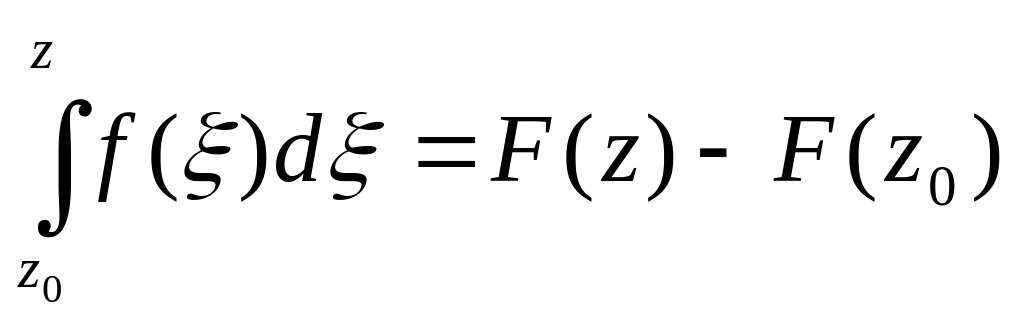
Таблица интегралов аналогична вещественным переменным.

17. Интегральная формула Коши. Ряды Тейлора и Лорана. Физический смысл аналитической функции.

Интегральная формула Коши. Пусть функция аналитическая в области Д замкнутой односвязной и L граница области, тогда выполняется , где , а интегрирование в положительном направление.

Эта формула позволяет находить в произвольной точки через её значение на границе.

Ряд Лорана.

Всякая аналитическая функция в кольце , может быть разложено в ряд Лорана:

, где , L – кривая, лежащая внутри кольца.

Ряд Тейлора.

Если аналитична в точке , вытекает разложение в ряд Тейлора:

Физический смысл аналитической функции.

Всякая аналитическая функция определяет некоторое движение идеальное несжимаемое, это движение двухмерное и безвихревое .

18. Классификация особых точек аналитической функции. Вычисление вычета в полюсе. Теорема о вычетах.

Особая точка называется изолированной особой точкой аналитической функции , если в некоторой окрестности этой точки нет других особых точек.

Особая точка может быть в случае или - не существует.

Если особая изолированная точка , то , что .

Разлагается в этом кольце в ряд Лорана:

Правильная часть главная часть

Если нет членов с отрицательными показателями, то точку называют устранимой.

Если имеется конечное число членов с отрицательными степенями, причем наибольшая отрицательная степень имеет вид , то точка - полюс m-того порядка.

Если в разложение есть бесконечное число членов с отрицательными степенями, то точка - называется существенно особенной точкой функции .

Если , то - полюс

Если - не существует, то - существенно особенная.

Вычет аналитической функции в изолированной точки - является комплексным числом . L – окружность в положительном направление с центром в и лежащая в кольце , в котором функция аналитична.

Т.Коши о вычете. Если функция является аналитической в , ограничена контуром L, за исключением конечного число изолированных особых точек , лежащих внутри , то интеграл